Exponenta Banner

spdiags

Извлеките ненулевые диагонали и создайте разреженные полосы и диагональные матрицы

Свернуть все на странице

Синтаксис

Bout = spdiags(A)
[Bout,id] = spdiags(A)
Bout = spdiags(A,d)
S = spdiags(Bin,d,m,n)
S = spdiags(Bin,d,A)

Описание

пример

Bout = spdiags(A) извлекает ненулевые диагонали из m-by- n матрица A и возвращает их как столбцы в min(m,n)-by- p матрица Bout, где p - количество ненулевых диагоналей.

пример

[Bout,id] = spdiags(A) также возвращает диагональные числа id для ненулевых диагоналей в A. Размер Bout является min(m,n)-by- length(id).

пример

Bout = spdiags(A,d) извлекает диагонали в A определяется d и возвращает их как столбцы min(m,n)-by- length(d) матрица Bout.

пример

S = spdiags(Bin,d,m,n) создает m-by- n разреженная матрица S взяв столбцы Bin и размещение их по диагоналям, заданным d.

пример

S = spdiags(Bin,d,A) заменяет диагонали в A определяется d со столбцами Bin.

Примеры

свернуть все

Открыть Live Script

Создайте тридиагональную матрицу с помощью трех векторов, измените некоторые диагонали матрицы, а затем извлеките диагонали.

Создайте вектор 9 на 1 из них, а затем создайте тридиагональную матрицу с помощью вектора. Просмотрите элементы матрицы.

n = 9;
e = ones(n,1);
A = spdiags([e -2*e e],-1:1,n,n);
full(A)
ans = 9×9

    -2     1     0     0     0     0     0     0     0
     1    -2     1     0     0     0     0     0     0
     0     1    -2     1     0     0     0     0     0
     0     0     1    -2     1     0     0     0     0
     0     0     0     1    -2     1     0     0     0
     0     0     0     0     1    -2     1     0     0
     0     0     0     0     0     1    -2     1     0
     0     0     0     0     0     0     1    -2     1
     0     0     0     0     0     0     0     1    -2

Измените значения на основной (d = 0) диагональ A.

Bin = abs(-(n-1)/2:(n-1)/2)';
d = 0;
A = spdiags(Bin,d,A);
full(A)
ans = 9×9

     4     1     0     0     0     0     0     0     0
     1     3     1     0     0     0     0     0     0
     0     1     2     1     0     0     0     0     0
     0     0     1     1     1     0     0     0     0
     0     0     0     1     0     1     0     0     0
     0     0     0     0     1     1     1     0     0
     0     0     0     0     0     1     2     1     0
     0     0     0     0     0     0     1     3     1
     0     0     0     0     0     0     0     1     4

Наконец, восстановите диагонали A как столбцы в матрице.

Bout = spdiags(A);
full(Bout)
ans = 9×3

     1     4     0
     1     3     1
     1     2     1
     1     1     1
     1     0     1
     1     1     1
     1     2     1
     1     3     1
     0     4     1
Открыть Live Script

Извлеките ненулевые диагонали матрицы и исследуйте выходной формат spdiags.

Создайте матрицу, содержащую смесь ненулевых и нулевых диагоналей.

A = [0     5     0    10     0     0
     0     0     6     0    11     0
     3     0     0     7     0    12
     1     4     0     0     8     0
     0     2     5     0     0     9];

Извлеките ненулевые диагонали из матрицы. Задайте два выхода, чтобы вернуть диагональные числа.

[Bout,d] = spdiags(A)
Bout = 5×4

     0     0     5    10
     0     0     6    11
     0     3     7    12
     1     4     8     0
     2     5     9     0


d = 4×1

    -3
    -2
     1
     3

Столбцы первого выходного Bout содержат ненулевые диагонали A. Второй выходной d В перечислены индексы ненулевых диагоналей A. Самая длинная ненулевая диагональ в A находится в столбце 3 Bout. Чтобы задать все столбцы Bout ту же длину, другие ненулевые диагонали A добавить дополнительные нули в соответствующие столбцы в Bout. Для m-by- n матрицы с m < n, правила:

  • Для ненулевых диагоналей ниже основной диагонали A, дополнительные нули складываются в верхах столбцов (как в первых двух столбцах Bout).

  • Для ненулевых диагоналей выше основной диагонали A, дополнительные нули складываются в нижней части столбцов (как в последнем столбце Bout).

spdiags прокладки Bout с нулями таким образом, даже если самая длинная диагональ не возвращается в Bout.

Открыть Live Script

Создайте случайную матрицу 5 на 5.

A = randi(10,5,5)
A = 5×5

     9     1     2     2     7
    10     3    10     5     1
     2     6    10    10     9
    10    10     5     8    10
     7    10     9    10     7

Извлеките основную диагональ, и первые диагонали выше и ниже нее.

d = [-1 0 1];
Bout = spdiags(A,d)
Bout = 5×3

    10     9     0
     6     3     1
     5    10    10
    10     8    10
     0     7    10

Попробуйте извлечь пятую супердиагональную (d = 5). Потому что A имеет только четыре супердиагонали, spdiags возвращает диагональ как все нули той же длины, что и основная (d = 0) диагональ.

B5 = spdiags(A,5)
B5 = 5×1

     0
     0
     0
     0
     0
Открыть Live Script

Исследуйте, как spdiags создает диагонали, когда столбцы матрицы входа длиннее, чем диагонали, которые они заменяют.

Создайте матрицу 6 на 7 из чисел с 1 по 6.

Bin = repmat((1:6)',[1 7])
Bin = 6×7

     1     1     1     1     1     1     1
     2     2     2     2     2     2     2
     3     3     3     3     3     3     3
     4     4     4     4     4     4     4
     5     5     5     5     5     5     5
     6     6     6     6     6     6     6

Использование spdiags чтобы создать квадратную матрицу 6 на 6 с несколькими столбцами Bin как диагонали. Поскольку некоторые диагонали имеют только один или два элемента, существует несоответствие размеров между столбцами в Bin и диагонали в A.

d = [-4 -2 -1 0 3 4 5];
A = spdiags(Bin,d,6,6);
full(A)
ans = 6×6

     1     0     0     4     5     6
     1     2     0     0     5     6
     1     2     3     0     0     6
     0     2     3     4     0     0
     1     0     3     4     5     0
     0     2     0     4     5     6

Каждый из столбцов в Bin имеет шесть элементов, но только основную диагональ в A имеет шесть элементов. Поэтому все другие диагонали в A обрезать элементы в столбцах Bin так, чтобы они помещались на выбранных диагоналях:

Путь spdiags обрезает диагонали в зависимости от размера m-by- n матрица A. Когда m≥n, поведение такое, как изображено выше:

  • Диагонали ниже основной диагонали берут сначала элементы с верхних частей столбцов.

  • Диагонали выше основной диагонали берут сначала элементы из днищ столбцов.

Это поведение отменяется, когда m<n:

A = spdiags(Bin,d,5,6);
full(A)
ans = 5×6

     1     0     0     1     1     1
     2     2     0     0     2     2
     3     3     3     0     0     3
     0     4     4     4     0     0
     5     0     5     5     5     0

  • Диагонали выше основной диагонали берут сначала элементы с верхних частей столбцов.

  • Диагонали ниже основной диагонали берут сначала элементы из днищ столбцов.

Входные параметры

свернуть все

Входная матрица. Эта матрица обычно (но не обязательно) разрежена.

Типы данных: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical
Поддержка комплексного числа: Да

Диагональные числа, заданные как скаляр или вектор положительных целых чисел. Диагональные числа следуют тем же соглашениям, что и diag:

  • d < 0 ниже основной диагонали и удовлетворяет d >= -(m-1).

  • d = 0 является основной диагональю.

  • d > 0 выше основной диагонали и удовлетворяет d <= (n-1).

Система координат m-by- n матрица A имеет (m + n - 1) диагонали. Эти диагонали заданы в векторе d использование индексов из -(m-1) на (n-1). Для примера, если A является 5 на 6, имеет 10 диагоналей, которые заданы в векторе d использование индексов -4, -3,... 4, 5. Следующая схема иллюстрирует эту диагональную нумерацию.

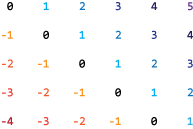
Если вы задаете диагональ, которая лежит вне A (такие как d = 7 в примере выше), затем spdiags возвращает эту диагональ как все нули.

Пример: spdiags(A,[3 5]) извлекает третью и пятую диагонали из A.

Диагональные элементы, заданные как матрица. Эта матрица обычно (но не обязательно) полна. spdiags использует столбцы Bin для замены указанных диагоналей в A. Если требуемый размер выхода m-by- n, затем Bin должно иметь min(m,n) столбцы.

С синтаксисом S = spdiags(Bin,d,m,n), если столбец Bin имеет больше элементов, чем диагональ, которую он заменяет, и m >= n, затем spdiags берёт элементы супердиагоналей из нижней части столбца Bin, и элементы поддиагоналей из верхней части столбца Bin. Однако, если m < n , затем супердиагонали из верхней части столбца Bin, и поддиагонали из нижней части. Пример такого поведения см. в Столбцах и Диагоналях Разных Размеров.

Типы данных: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical
Поддержка комплексного числа: Да

Размерности, заданные как неотрицательные скалярные целые числа. spdiags использует эти входы, чтобы определить, как большую матрицу создать.

Пример: spdiags(Bin,d,300,400) создает матрицу 300 на 400 с столбцами B расположенные по заданным диагоналям d.

Выходные аргументы

свернуть все

Диагональные элементы, возвращенные как полная матрица. Столбцы Bout содержат диагонали, извлеченные из A. Любые элементы Bout соответствует положениям вне A равны нулю.

Диагональные числа, возвращенные как вектор-столбец. См. d описание диагональной нумерации.

Выходная матрица. S принимает одну из двух форм:

  • С S = spdiags(Bin,d,A), указанные диагонали в A заменяются столбцами в Bin для создания S.

  • С S = spdiags(Bin,d,m,n), а m-by- n разреженная матрица S формируется путем взятия столбцов Bin и размещение их по диагоналям, заданным d.

Расширенные возможности

Генерация кода C/C + +
Сгенерируйте код C и C++ с помощью Coder™ MATLAB ®

.

См. также

|

Представлено до R2006a

Документация MATLAB

Поддержка