Исследуйте локальные типы моделей

Альтернативные локальные типы моделей

Сначала попробуйте подгонять значения по умолчанию с помощью Fit models кнопки общей задачи.

Если вы хотите попробовать альтернативные локальные типы модели, выберите узел отклика, затем на панели Common Tasks нажмите New Local Model. Это открывает диалоговое окно Настройка локальной модели (Local Model Setup). Просмотрите типы моделей на этой странице.

Чтобы изучить подгонку, см. «Оценка локальных моделей».

Доступные модели зависят от количества входных факторов. Полином, полиномиальный сплайн, усеченный силовой ряд, сплайн свободного узла и модели роста предназначены только для одного фактора.

Дополнительные функции отклика можно выбрать на этом этапе с помощью вкладки Response Features диалогового окна Настройка локальной модели (Local Model Setup). Их также можно добавить позже. Model Browser выбирает достаточные функции отклика для текущей модели.

Для получения статистической информации и доступных функций отклика см. каждый тип локальной модели.

См. также

Класс локальной модели: полиномы и полиномиальные сплайны

Полиномы

На локальном уровне, если у вас есть один входной коэффициент, можно выбрать полином непосредственно из списка локальных классов модели. Здесь можно выбрать порядок используемых полиномов, и можно задать модель данной величины для этого вида локальной модели.

Если существует более одного входного фактора, можно выбрать Линейные модели из списка Класс локальной модели, тогда можно выбрать Полином или Гибридный сплайн. Это другая полиномиальная модель, в которой можно изменить больше настроек, таких как Stepwise, Редактор (где можно удалить любые модельные условия), и можно выбрать различные порядки для различных факторов (как с глобальными уровневыми полиномиальными моделями). См. класс локальной модели: линейные модели.

Для этой полиномиальной модели и Линейных моделей: Выбор полинома доступны различные функции отклика. Просмотреть их можно, щелкнув вкладку Response Features в диалоговом окне Настройка локальной модели (Local Model Setup). Полиномы с одним входом могут иметь модель данной величины, и можно задать характеристики отклика относительно данной величины. См. «Опорные модели».

Для класса полиномиальной модели разрешены следующие функции отклика:

Расположение максимального или минимального значения.
Значение функции аппроксимации в заданной пользователем x-ordinate. Когда используются данные величины модели, значение соответствует данной величине (для примера, mbt - x).
N^th производная в заданной пользователем x-ординате, для n = 1, 2,..., d, где d - степень полинома.

Смотрите раздел глобальной модели Полиномы для общего описания полиномиальных моделей.

Полиномиальный сплайн

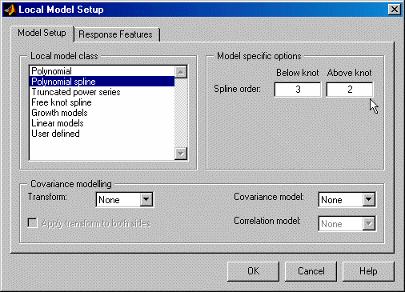
Сплайн является кусочным полиномом, где различные сечения полинома сгруппированы гладко. Расположение каждого пропуска называется узлом. Полиномиальные сплайны необходимы для моделирования кривых крутящего момента/искры.

Эта модель имеет только один узел. Можно выбрать порядки полиномов выше и ниже узла. См. также раздел Гибридные сплайны. Эти глобальные модели также используют сплайны, но используют тот же полином порядка по всему.

Полиномиальные сплайны доступны только для одиночных входных факторов. В следующем примере показан типовой крутящий момент/искровая кривая, которая требует правильной аппроксимации сплайна. Узел показан в виде красного пятна на максимуме, а кривизна выше и ниже узла отличается. В этом случае существует кубическая функция базиса ниже узла и квадратичная выше.

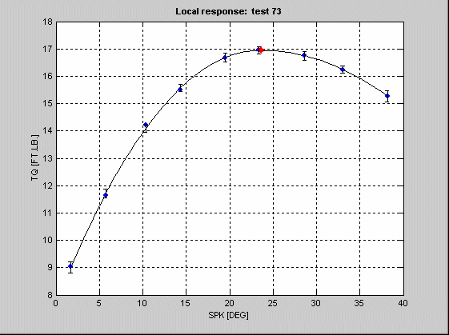
Чтобы смоделировать отклики, которые характеризуются внешним видом одной и четко определенной стационарной точкой с асимметричной кривизной с каждой стороны локального минимума или максимума, задайте следующий класс сплайна,

где k - расположение узла, обозначает коэффициент регрессии,,.

где c - заданная пользователем степень для левого полинома, h - заданная пользователем степень для правого полинома, а нижние индексы Low и High обозначают слева (ниже) и справа (выше) узел, соответственно.

Исключение членов в и гарантирует, что первая производная в положении узла непрерывна. В сложение, по определению константа должна быть равна значению функции аппроксимации в узле, то есть значению в стационарной точке.

Для этого класса модели функции отклика могут быть выбраны как

Подгонка констант
Положение узла
Значение функции аппроксимации в заданной пользователем дельте
из положения узла, если задан опорный элемент, в противном случае значение является абсолютным.
Различие между значением функции аппроксимации в заданной пользователем дельте из положения узла и значением функции аппроксимации в узле

Класс локальной модели: линейные модели

Выберите Linear Models а затем нажмите Setup.

Теперь можно настроить полином или гибридные сплайны моделей. Настройки в точности совпадают с настройками глобальных линейных моделей.

Эти модели предназначены для нескольких входных факторов - для одинарных входных факторов можно использовать другую полиномиальную модель из списка Local Model Class, где можно только изменить полином порядка. См. класс локальной модели: полиномы и полиномиальные сплайны.

Если существует более одного входного фактора, можно выбрать Линейные модели из списка Класс локальной модели, тогда можно выбрать Полином или Гибридный сплайн. Этот полином является другой моделью, где можно изменить больше настроек, таких как Stepwise, Редактор (где можно удалить любые модельные условия), и можно выбрать различные порядки для различных факторов (как с глобальными полиномиальными моделями уровня).

Для получения дополнительной информации смотрите Глобальные линейные модели: полиномы и гибридные сплайны.

По умолчанию входы преобразуются в [-1, 1] перед аппроксимацией и оценкой полиномов. Это важно, так как различия в шкалах между входами могут вызвать числовые проблемы. Обычно рекомендуется преобразовать входы, так как это облегчает проблемы с переменными разной шкалы. В некоторых обстоятельствах вы можете быть обеспокоены значениями полиномов (для примера, если ваша стратегия требует необработанных полиномиальных коэффициентов). В этом случае можно снять флажок Transform input range, чтобы использовать нетрансформированные модули для вычисления естественных полиномов.

Для этой Линейной Модели доступны различные функции отклика: Полиномиальная модель и другой Полиномиальный выбор (для одинарных входных факторов). Просмотреть их можно, щелкнув вкладку Response Features в диалоговом окне Настройка локальной модели (Local Model Setup). Полиномы с одним входом могут иметь модель данной величины, и можно задать характеристики отклика относительно данной величины. См. «Опорные модели».

Эти линейные модели маркированы Quadratic, Cubic, и так далее, на блоке плана тестирования. Один входной тип полиномов помечен Poly2, Poly3и так далее. Для высших порядков оба типа маркируются Poly н.

Класс локальной модели: усеченная степень

Это доступно только для одного входного фактора.

Можно выбрать порядок полиномиального базиса функции и количество узлов для усеченных базовых сплайнов Power Series. Сплайн является кусочным полиномом, где различные сечения полинома сгруппированы гладко. Точка каждого пропуска называется узлом. Усеченный ряд степеней изменяет коэффициент для самой высокой мощности, когда вход проходит выше значения узла.

Это усечено, потому что степенный ряд является приближением к бесконечной сумме полиномиальных членов. Можно использовать бесконечные суммы для аппроксимации произвольных функций, но явно невозможно соответствовать всем коэффициентам.

Щелкните Polynomial, чтобы увидеть (и удалить, если хотите) полиномиальные условия. Одно из применений функции удаления полинома состоит в том, чтобы сделать функцию линейной до узла, а затем квадратичной над узлом. В этом случае удалите квадратичный коэффициент.

См. также

Полином Сплайн, где можно выбрать различные базисные функции порядка с каждой стороны узла
Гибридные сплайны, глобальная модель, где можно выбрать порядок сплайна для одного из факторов (остальные имеют установленные полиномы)
Класс локальной модели: сплайн свободного узла, сплайны свободного узла, где можно выбрать количество узлов и порядок базовых функций

Сплайны с усеченным Степенью базисом (TPSBS)

Общий класс сплайн функций с произвольной (но строго увеличивающейся) последовательностью узлов:

Это задает сплайн порядка m с последовательностью узлов

Для этого класса модели функции отклика могут быть выбраны как

Подгонка констант
Вектор положения узла.
Значение функции аппроксимации при заданном пользователем значении
Значение n^th производные сглаженной функции относительно _xj при заданном пользователем значении с n = 1, 2,..., m-2

Можно удалить из модели любой из полиномиальных членов.

Класс локальной модели: сплайн свободного узла

Это те же самые, что и класс глобальной модели: сплайн свободного узла (который также доступен только для одного входного фактора). Для примера формы кривой см. глобальные сплайны свободного узла.

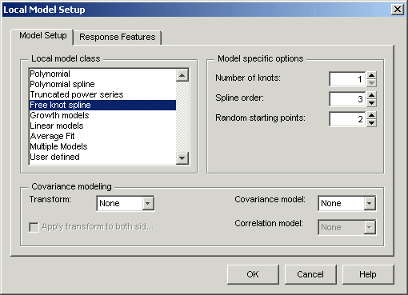
Сплайн является кусочным полиномом, где различные сечения полинома сгруппированы гладко. Точка соединения называется узлом.

Можно выбрать количество узлов. Можно выбрать порядок расположения полинома (во всех сечениях кривых) от 1 до 3. Значение по умолчанию является кубическим.

Можно задать количество Random starting points. Это количество начальных догадок в положениях узлов.

См. также

Полином Сплайн, где можно выбрать различные базисные функции порядка для каждой стороны узла
Класс локальной модели: усеченный силовой ряд, где можно выбрать порядок основной функции
Гибридные сплайны, глобальная модель, где можно выбрать порядок сплайна для одного из факторов (остальные имеют установленные полиномы)

Свободные узловые сплайны

Этот базис не является наиболее подходящим для целей оценки и оценки, поскольку матрица проекта может быть плохо обусловлена. В сложение, количество арифметических операций, необходимых для оценки функции сплайна, зависит от местоположения относительно узлов. Эти свойства могут привести к числовым неточностям, особенно когда количество узлов большое. Можно уменьшить такие проблемы, используя B-сплайны.

Наиболее важным аспектом является то, что для умеренных m расчетная матрица, выраженная в терминах B-сплайнов, относительно хорошо обусловлена.

Для этого класса модели функции отклика могут быть выбраны как

Подгонка констант
Вектор положения узла.

Значение функции аппроксимации при заданном пользователем значении

Класс локальной модели: модели роста

Модели роста имеют несколько доступных сортов. Они доступны только для отдельных входных факторов.

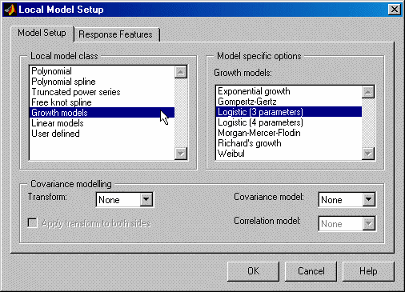
Это все разновидности сигмоидальных кривых между двумя асимптотами, как в следующем примере.

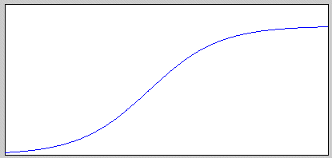
Модели роста часто являются наиболее подходящей формой кривой для моделирования двигателя заряда воздуха.

Математические детали о различиях между этими моделями роста см. в следующих разделах:

Логистическая модель трех параметров
Модель Моргана-Мерсера-Флодина
Четырехпараметрическая логистическая кривая
Кривые Ричардса
Кривая роста Вейбула
Экспоненциальная кривая роста
Модель роста Gompertz

Логистическая модель трех параметров

Уравнение $y_{j} = \frac{α}{1 + \exp {[- κ (x_{j} - γ)]}^{r}}$ задает логистическую кривую трех параметров.

где достигается окончательный размер, $Κ$ является параметром шкалы и является x-ординатой точки перегиба кривой.

Кривая имеет асимптоты _yj = 0 как _xj $\to$ - ∞ и как _xj $\to$ ∞. Скорость роста на максимуме, когда _yj = α/2, что происходит, когда _xj = $γ$ . Максимальная скорость роста соответствует

К коэффициентам аппроксимации применяются следующие ограничения:

α > 0, $Κ > 0$ , $γ > 0$ .

Вектор функции отклика g для трех параметров логистическая функция определяется как

$g = {[\begin{matrix} α & γ & κ & \frac{κ α}{4} \end{matrix}]}^{Τ}$

Модель Моргана-Мерсера-Флодина

Это уравнение задает модель роста Моргана-Мерсера-Флодина (MMF).

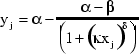
где α - значение верхней асимптоты, β - значение нижней асимптоты, $Κ$ измеряющий параметр, и δ - параметр, который управляет местоположением точки перегиба для кривой. Точка перегиба расположена в

для

Не существует точки перегиба для и < 1. Все кривые MMF являются сублогистическими, в том смысле, что точка флексии всегда находится ниже 50% роста (0.5α). Следующие ограничения применяются к значениям коэффициентов аппроксимации:

α > 0, β > 0, $Κ$ > 0, δ > 0
α > β

Это уравнение предоставляет вектор функции отклика g.

$g = {[\begin{matrix} α & β & κ & δ & \frac{δ - 1}{2 δ} \end{matrix}]}^{Τ}$

Четырехпараметрическая логистическая кривая

Это уравнение задает логистическую модель с четырьмя параметрами.

$β - \frac{(α - β)}{(1 + \frac{e^{γ κ}}{x^{κ}})}$

с ограничениями, и. Снова, является значением верхней асимптоты, является масштабным фактором и является фактором, который находит x-ординату точки перегиба в

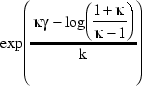
Следующие ограничения применяются к значениям коэффициентов аппроксимации:

Все параметры > 0
α > β

Это доступный вектор функции отклика:

$g = {[\begin{matrix} α & β & κ & γ & \frac{(κ γ - \log (\frac{1 + κ}{κ - 1}))}{κ} \end{matrix}]}^{Τ}$

Кривые Ричардса

Это уравнение задает семейство кривых Ричардса моделей роста.

δ ≠ 1

где α - верхняя асимптота, $γ$ - расположение точки перегиба на оси X, $Κ$ коэффициент масштабирования, и δ - параметр, который косвенно определяет местонахождение точки перегиба.

Y-ордината точки перегиба определяется из

Ричардс также вывел средний нормированный темп роста для кривой как

Следующие ограничения применяются к значениям коэффициентов аппроксимации:

α > 0, $γ$ > 0, $Κ$ > 0, δ > 0
α > $γ$
δ ≠ 1

Наконец, вектор функции отклика g для семейства кривых роста Ричардса определяется как

$g = {[\begin{matrix} α & γ & κ & \frac{κ}{2 (δ + 1)} \end{matrix}]}^{T}$

Кривая роста Вейбула

Это уравнение задает кривую роста Вейбула.

где - значение асимптоты верхней кривой, - значение асимптоты нижней кривой, - параметр масштабирования и - параметр, который управляет x-ординатой для точки перегиба кривой,

К параметрам подгонки кривых применяются следующие ограничения:

α > 0, β > 0, $Κ$ > 0, δ > 0
α > β

Связанный вектор функции отклика

$g = {[\begin{matrix} α & β & κ & δ & (\frac{1}{κ}) {(\frac{δ - 1}{δ})}^{1 / δ} \end{matrix}]}^{Τ}$

Экспоненциальная кривая роста

Это уравнение задает экспоненциальную модель роста.

где α - значение верхней асимптоты, β - начальный размер, и $Κ$ является параметром шкалы (временная константа, контролирующая скорость роста). К коэффициентам аппроксимации применяются следующие ограничения:

α > 0, β > 0, $Κ$ > 0
α > β

Вектор функции отклика g для экспоненциальной модели роста определяется как

Модель роста Gompertz

Другой полезной формулировкой, которая не показывает симметричную точку флексии, является модель роста Гомперца. Определяющее уравнение

где α - конечный размер, $Κ$ является масштабным коэффициентом, и $γ$ - x-ордината точки флексии. Соответствующая y-ордината точки перегиба происходит в

С максимальными темпами роста

Следующие ограничения применяются к выбору значений параметров для модели Гомперца:

α > 0, $Κ$ > 0, $γ$ > 0.

Вектор функции отклика g для модели роста Gompertz определяется как

$g = {[\begin{matrix} α & γ & κ & \frac{κ α}{e} \end{matrix}]}^{Τ}$

Класс локальной модели: пользовательские модели

Можно создать пользовательские модели для использования в локальных, глобальных или одноэтапных моделях.

Определяемый пользователем тип модели позволяет вам задать уравнение в файле, который будет использоваться для подбора кривой в тулбоксе.

Чтобы создать и сдать на хранение пользовательскую модель:

Скопируйте пользовательский файл шаблона (functemplate.m) в местоположение на MATLAB^® путь (но не ниже matlabroot\ toolbox\mbc). Найти файл в этом месте:
```
<matlabroot>\toolbox\mbc\mbcmodels\@xregusermod\functemplate.m
```
Измените копию файла шаблона для модели. Кодируйте все обязательные функции. Комментарии к шаблону описывают все обязательные и дополнительные функции.
Не обязательно изменять каждый дополнительный раздел. Если вы не хотите использовать дополнительный раздел, оставьте его неизмененным.
Проверьте свою модель в тулбокс с помощью этой команды:
```
m = checkin(xregusermod,'MfileName',TestInputData)
```

Примечание

Ваши пользовательские модели могут иметь столько факторов, сколько вы выберете.

После сдачи на хранение пользовательских моделей они появляются как опции в диалоговом окне Настройка модели (Model Setup), когда вы используете данные с нужным количеством факторов.

Чтобы удалить зарегистрированную модель из тулбокса, введите:

remove(xregusermod,'MfileName')

Примечание

Если какая-либо из ваших глобальных моделей определена пользователем, вы не можете использовать MLE (максимальную оценку правдоподобия) для вашей двухэтапной модели.

Можно изучить этот пример пользовательского файла модели как руководство:

<MATLAB root>\toolbox\mbc\mbcmodels\@xregusermod\weibul.m

Этот файл определяет локальную модель Weibul (модель роста) в тулбоксе и, следовательно, не должен быть изменен. Убедитесь, что файл не перезаписан. Если вы измените файл, сохраните его под другим именем.

Следующие разделы объясняют, как изучить и проверить в модели Вейбула:

Исследуйте пример пользовательской модели
Проверьте модель в тулбокс
Проверьте, что модель сдана на хранение
Восстановление после ошибок редактирования

Исследуйте пример пользовательской модели

Этот пример демонстрирует, как создать пользовательскую модель для функции Weibul:

y = alpha - (alpha - beta).*exp(-(kappa.*x).^delta)

Откройте следующий файл примера

<MATLAB root>\toolbox\mbc\mbcmodels\@xregusermod\weibul.m

Обратите внимание, что файл вызывается тулбоксом с помощью

varargout= weibul(m,x,varargin)

Где переменные заданы как

m = the xregusermod object
x = input data as a column vector for fast eval

Первая функция в файле шаблона является векторизованной оценкой функции. Во-первых, параметры модели извлекаются:

b= double(m);

Затем происходит оценка:

y = b(1) - (b(1)-b(2)).*exp(-(b(3).*x).^b(4));

Примечание

Параметры всегда указываются и объявляются в том же порядке.

Обязательные локальные функции. Отредактируйте эти локальные функции следующим образом:

Введите количество коэффициентов входа. Для функций y = f (x) это 1.

function n= i_nfactors(U,b)
n= 1;

Введите количество настроенных параметров. В этом примере в модели Weibul есть четыре параметра.

function n= i_numparams(U,b)
n= 4;

Следующая локальная функция возвращает вектор-столбец начальных значений (param) для соответствия параметров. Начальные значения могут быть определены как зависящие от данных; следовательно, существует флаг, который должен сигнализировать, не стоит ли подгонять данные (OK). В weibul.m существует стандартная программа для вычисления зависящей от данных оценки начального параметра. Если данные не предоставлены, используются значения параметров по умолчанию.

function [param,OK]= i_initial(U,b,X,Y)
param= [2 1 2 5]';
OK=1;

Дополнительные локальные функции. Для установки дополнительных параметров можно использовать следующие дополнительные локальные функции

Можно указать нижнюю и верхнюю границы для параметров модели. Эти ограничения появляются в том же порядке, в котором параметры объявлены и используются во всем файле шаблона.
```
function [LB,UB,A,c,nlcon,optparams]=i_constraints(U,b,varargin)
LB=[eps eps eps eps]';
UB=[1e10 1e10 1e10 1e10]';
```
Можно также задать линейные ограничения параметров. Этот код создает ограничение (-alpha + beta) меньше или равно нулю:
```
A= [-1 1 0 0];
c= [0];
```
nlcon определяет количество нелинейных ограничений (здесь объявлено равным нулю). Если количество нелинейных ограничений не равняется нулю, нелинейные ограничения вычисляются в i_nlconstraints.
```
nlcon= 0;
```
optparams задает любые необязательные параметры. Дополнительные параметры для функции затрат не объявлены.
```
optparams= [];
```
i_foptions определяет опции подгонки. Опции подгонки всегда основаны на входе fopts. Смотрите справку MATLAB на optimset или optimoptions для получения дополнительной информации об опциях подгонки. Когда ограничений нет, тулбокс использует функцию MATLAB lsqnonlin для подбора кривой, в противном случае fmincon используется.
```
function fopts= i_foptions(U,b,fopts)

	fopts= optimset(fopts,'Display','none');
```

i_jacobian может предоставить аналитический якобиан, чтобы ускорить алгоритм аппроксимации.

function J= i_jacobian(U,b,x)

	x = x(:);
	J= zeros(length(x),4);

	a=b(1); beta=b(2); k=b(3); d=b(4);

	ekd= exp(-(k.*x).^d);
	j2= (a-beta).*(k.*x).^d.*ekd;

	J(:,1)= 1-ekd;
	J(:,2)= ekd;
	J(:,3)= j2.*d./k;
	J(:,4)= j2.*log(k.*x);

i_labels определяет метки, используемые на графиках. Можно использовать LaTeX обозначения и он форматирован.
```
function c= i_labels(U,b)
c={'\alpha','\beta','\kappa','\delta'};
```
i_char - строка экранного уравнения, которая может содержать выражения LaTeX. Появляются текущие значения параметров модели.
```
function str= i_char(U,b)

s= get(U,'symbol');
str=sprintf('%.3g - (%.3g-%.3g)*exp(-(%.3g*x)^{%.3g})',...
		b([1 1 2 3]), detex(s{1}), b(4));
```

i_str_func отображает определение функции с метками, появляющимися вместо параметров (а не числовых значений).

function str= i_str_func(U,b, TeX)

s= get(U,'symbol');
if nargin == 2 || TeX
	s = detex(s)
end
% This can contain TeX expressions supported by HG text objects
lab= labels(U);
str= sprintf('%s - (%s - %s)*exp(-(%s*%s)^{%s})',...
		lab{1},lab{1},lab{2},lab{3},s{1},lab{4});

i_rfnames задает имена функции отклика. Этот пример показывает определенная функция отклика, который не является одним из параметров (в этом случае он также нелинейен).
Вам не нужно определять rname (он может вернуть пустой массив ячеек).
```
function [rname, default] = i_rfnames(U,b)
% response feature names 
rname= {'inflex'};
      
if nargout>1
    default = [1 2 5 4]; %{'Alpha','Beta','Inflex','Delta'};
end
```

i_rfvals задает значения функций отклика. Этот пример определяет функцию отклика, помеченный как INFLEX на предыдущем шаге. Матрица Якобия также определяется здесь как dG.

function [rf,dG]= i_rfvals(U,b) 
%I_RECONSTRUCT nonlinear reconstruction
%
% p = i_reconstruct(m,b,Yrf,dG,rfuser)
%  Inputs
%     Yrf   response feature values
%     dG    Jacobian of response features with respect to
%              parameters
%     rfuser index to the user-defined response features
%              so you can find out which response features
%              are which. rfuser(i) = 0 if the rf is a parameter.
%
% If all response features are linear in model parameters
%  then you do not need to define 'i_reconstruct'. 

% this is an example of how to implement a nonlinear response
% feature definition

K = b(3);
D = b(4);
if D>=1
   rf= (1/K)*((D-1)/D)^(1/D);
else
   rf= NaN;
end
      
if nargout>1
   % Jacobian of response features with respect to model 
   %  parameters
   if D>=1
      dG= [0, 0, -((D-1)/D)^(1/D)/K^2,...
            1/K*((D-1)/D)^(1/D)*(-1/D^2*log((D-1)/D)+...
            (1/D-(D-1)/D^2)/(D-1))];   
   else
      dG= [0, 0, 1 1];
   end
end

The i_reconstruct локальная функция позволяет восстановить параметры модели из заданных функций отклика. Если все функции отклика линейны в параметрах, то вам не нужно задавать эту функцию. Код сначала определяет, какие функции отклика (если таковые имеются) определены пользователем.

function p= i_reconstruct(U,b,Yrf,dG,rfuser) 
%I_RECONSTRUCT nonlinear reconstruction
%
% p = i_reconstruct(m,b,Yrf,dG,rfuser)
%  Inputs
%     Yrf   response feature values
%     dG    default Jacobian of response features
%     rfuser index to the user-defined response features so you can find
%     out which response features are which. rfuser(i) = 0 if the
%     rf is a parameter.
%
% If all response features are linear in model parameters then you do not
% need to define 'i_reconstruct'. 

% reconstruct linear response features using this line
p= Yrf/dG';

% find which response feature is a nonlinear user-defined response feature
f= rfuser>size(p,2);
if ~any(rfuser==3)
   % need to use delta (must be > 1) for reconstruction to work
   p(:,4)= max(p(:,4),1+16*eps);
   
   p(:,3)= ((p(:,4)-1)./p(:,4)).^(1./p(:,4))./Yrf(:,f);
end

Проверьте модель в тулбокс

После того, как вы создаете пользовательский файл модели, сохраните его где-то в пути.

Сдать на хранение модель. Процесс сдачи на хранение гарантирует, что заданная вами модель предоставляет интерфейс, который позволяет тулбоксу оценивать и подгонять его. Если процедура сдачи на хранение выполняется успешно, тулбокс регистрирует модель и делает ее доступной для подбора кривой при использовании соответствующих входных данных.

В командной строке, с файлом примера на пути, нужно создать модель и некоторые входные данные, затем вызвать checkin. Для пользовательской функции Weibul вызовите checkin с моделью примера, ее именем и некоторыми соответствующими данными.

checkin(xregusermod, 'weibul', [0.1:0.01:0.2]');

Это возвращает некоторые выходы командной строки, и появляется рисунок с именем модели и именами переменных, отображаемыми над графами входа и выхода оценки модели. Конечный вывод командной строки:

Model successfully registered for 
Model-Based Calibration Toolbox software.

Проверьте, что модель сдана на хранение

Чтобы убедиться, что определенная пользователем модель сдана на хранение в тулбокс:

Запустите Model Browser и загрузите данные, которые имеют необходимый формат для оценки пользовательской модели.
Настройте план тестирования с N Stage1 входные коэффициенты, где N количество входа факторов, определенных в i_nfactors.
Откройте диалоговое окно Настройка локальной модели (Local Model Setup) и выберите User-defined models в списке Класс локальной модели (Local Model Class). Определенная пользователем модель должна появиться в правом списке.

Чтобы проверить, что weibul пример пользовательской модели сдан на хранение:

Откройте gasoline_project.mat, и выберите PS22 план тестирования в дереве.
Дважды кликните значок Локальная модель (Local Model) в схеме плана тестирования.
В диалоговом окне Local Model Setup выберите User-defined models в списке Local Model Class. The Weibul пользовательская модель появится в правом списке, как сдано на хранение.

Восстановление после ошибок редактирования

Если вы изменяете файл, который задает возвращенную модель, которую вы используете в данный момент, Model Browser пытается продолжить.

Если у пользовательской модели есть серьезные ошибки (например, вы изменили количество входов или параметров, оценку модели или файл не может быть найден), Model Browser меняет статус текущей модели на 'Не подгонянный'.

Чтобы восстановить это состояние, сначала исправьте проблему в файле. Затем (для локальных моделей) можно выбрать Model > Fit Local для привязки. Вам не нужно снова проверять модель, но если у вас есть проблемы, сообщения об ошибке, полученные во время проверки, могут быть полезны при диагностике отказов.

Если существует незначительный отказ файла, то Model Browser продолжается, используя значения по умолчанию. Несущественные ошибки могут включать такие элементы, как определения меток, то есть отказы в i_char, i_label, i_str_func, или i_foptions. В командном окне появляется сообщение, содержащее подробную информацию об этих отказах.

Класс локальной модели: переходные модели

Используйте переходные модели для локальных, глобальных или одноэтапных моделей. Тулбокс поддерживает переходные модели с несколькими входными факторами, где время является одним из факторов. Можно задать динамическую модель с помощью Simulink^® программное обеспечение и файл, который описывает параметры для соответствия в этой модели. Тулбокс приводит пример под названием fuelPuddle который уже возвращен в тулбокс. Можно использовать этот пример для моделирования. Предоставленный пример требует двух входных факторов. Процесс создания и проверки собственных переходных моделей описан в следующих разделах на основе этого примера.

Создание папок
Создайте модель Simulink
Создайте пользовательский файл переходной модели
Обязательные локальные функции
Дополнительные локальные функции
Возврат в тулбокс
Использование и удаление переходных моделей

Найдите пример модели Simulink:

<MATLAB root>\toolbox\mbc\mbcsimulink\fuelPuddle

и пользовательский файл переходной модели:

<MATLAB root>\toolbox\mbc\mbcmodels\@xregtransient\fuelPuddle.m

Создание папок

Можно задать динамическую модель с помощью модели Simulink и пользовательского файла переходной модели, который описывает параметры, для соответствия в этой модели. Создайте папки для этих файлов, которые указаны в пути MATLAB. Затем необходимо проверить файлы в продукте Model-Based Calibration Toolbox™, прежде чем использовать их для моделирования.

Создайте папку и добавьте ее в путь MATLAB.
Для примера: D:\MyTransient.
Поместите свою модель Simulink в эту папку. См. «Создание модели Simulink».
Внутри новой папки создайте папку с именем @ xregtransient. (например, D :\MyTransient\@ xregtransient). Необходимо вызвать эту папку @ xregtransient.
Поместите пользовательский файл переходной модели в новую папку @ xregtransient. Этот файл должен иметь то же имя что и ваша модель Simulink. См. Создание пользовательского файла переходной модели.

Создайте модель Simulink

Создайте модель Simulink, чтобы представлять вашу переходную систему.

Входные порты Simulink представляют входы модели. Время является первым входом в модель в программном обеспечении Model-Based Calibration Toolbox, но не является входным портом в модели. Выход модели представлен выходом Simulink. В Model Browser поддерживается только один скалярный выход.

Ваша модель Simulink должна иметь некоторые свободные параметры, которые программное обеспечение Model-Based Calibration Toolbox будет соответствовать нелинейным методам наименьших квадратов. Используйте те же имена переменных в модели и пользовательский файл переходной модели.

Модель Simulink для fuelPuddle пример появляется на следующем рисунке. Вы исследуете файл примера (fuelPuddle.m) в более позднем разделе.

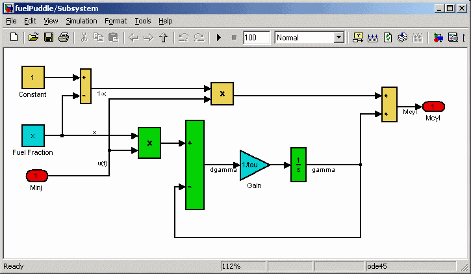
Метки блоков не важны. Модель возвращает один скалярный выход (здесь обозначенный "Mcyl”).

Тулбокс определяет параметры модели в Рабочем пространстве модели. Это можно увидеть в Model Explorer. Вектор всех параметров называется p также доступен.

Требования к модели. Как для непрерывных, так и для дискретных моделей применяются следующие правила:

Для моделей Simulink с решателем Fixed Step размер шага устанавливается на шаг расчета данных.
Для решателей Переменного шага размер шага симуляции задается моделью Simulink.
Вы видите ошибку, если размер выхода от симуляции модели Simulink не совпадает с размером входных данных, предоставляемых тулбоксом.

Создайте пользовательский файл переходной модели

Задайте файл переходной модели для модели Simulink, и этот файл должен иметь то же имя, что и ваша модель Simulink.

Скопируйте файл шаблона переходной модели, найденный в:
```
<MATLAB root>\toolbox\mbc\mbcmodels\@xregtransient\functemplate.m
```
Скопируйте файл в новое MyTransientfolder\ @ xregtransient папка, которую вы создали.
Измените копию файла шаблона для модели.
В коде с комментариями описываются обязательные и дополнительные функции, доступные в файле шаблона.
Вы не должны изменять каждый раздел. Если вы не хотите использовать дополнительный раздел, оставьте его неизмененным, и значения по умолчанию будут достаточными.

Откройте файл примера fuelPuddle.m (для fuelPuddle модель), чтобы изучить код, описанный в следующих разделах. Найдите файл здесь:

<MATLAB root>\toolbox\mbc\mbcmodels\@xregtransient\fuelPuddle.m

Обязательные локальные функции

Задайте следующие локальные функции:

Задайте параметры модели Simulink, для подгонки.
```
function vars= i_simvars(m,b,varargin);
vars = {'tau','x'};
```
Эта локальная функция должна вернуть массив ячеек из строк. Это имена параметров, которые требуются модели Simulink из рабочей области. Эти строки должны совпадать с именами параметров, объявленными в модели Simulink.
Если ваша модель Simulink требует, чтобы были определены постоянные параметры, сделайте это здесь:
```
function [vars,vals]= i_simconstants(m,b,varargin);
vars = {};
vals = [];
```
Это постоянные параметры, требуемые моделью Simulink из рабочей области, и не установлены. Эти параметры должны быть такими же, как и в модели Simulink, и все имена должны совпадать. Вот fuelPuddle не требует таких параметров и возвращает пустой массив ячеек и пустую матрицу.
Задайте Начальные условия для интеграторов.
```
function [ic]= i_initcond(m,b,X);
ic=[];
```
Начальные условия основаны на текущих параметрах, и здесь могут быть вычислены входы. Уход ic = [] означает, что Simulink использует определение начальных условий в модели Simulink.
Укажите количество факторов входа, включая время.
```
function n= i_nfactors(m,b);
n= 2;
```
Время является первым входом для переходных моделей. fuelPuddle имеет значение X = [t, u(t)], и поэтому количество факторов входа равно 2.
Эта локальная функция возвращает вектор-столбец начальных значений для подобранных параметров.
```
function [b0,OK]= i_initial(m,b,X,Y)
b0= [0.5 0.1]';
OK=1;
```
Проверяйте nargin перед использованием X и Y в качестве этой локальной функции вызывается с 2 или 4 параметрами: (m, b) или (m, b, X, Y).
Здесь можно выполнить некоторые вычисления, чтобы оценить хорошие начальные значения из данных X, Y. Начальные значения могут быть определены как зависящие от данных, поэтому существует флаг OK, который сигнализирует, если данные не стоят подгонки. Пример задает некоторые начальные значения по умолчанию для x и tau.

Дополнительные локальные функции

Вам не нужно редактировать оставшиеся локальные функции, если они не требуются. Комментарии в коде описывают роль каждой функции. Эти функции используются чаще всего при создании пользовательской модели (см. Класс локальной модели: Пользовательские модели).

Эти метки используются на графиках:

function c= i_labels(m,b)
b= {'\tau','x'};

Можно использовать обозначение LaTeX, и она правильно форматирована. По умолчанию имена переменных заданы в i_simvars используются для задания имен параметров.

Возврат в тулбокс

Создав модель Simulink и соответствующий файл функции, вы должны сохранить каждый на пути, как описано в Create Folders.

Чтобы убедиться, что заданная вами переходная модель предоставляет интерфейс, который позволяет тулбоксу оценивать и подгонять его, вы сдаете на хранение модель. Если эта процедура выполняется успешно, тулбокс регистрирует модель и делает ее доступной для подбора кривой при использовании соответствующих входных данных.

В командной строке, с файлом шаблона и моделями Simulink на пути, создайте некоторые входные данные, затем вызовите checkin. Следующая процедура.

Создайте некоторые соответствующие входные данные. Конкретные используемые данные не имеют значения; вы используете его только, чтобы проверить, может ли модель быть оценена.
Для fuelPuddle например, введите следующий вход в командной строке:
```
TestInputData = [0:0.1:10; ones(1,101)]';
```
Функции checkin с переходной моделью, ее именем и данными. В качестве примера введите:
```
m = checkin(xregtransient,'fuelPuddle',TestInputData)
```
Строка, которую вы используете для нового переходного имени модели, появляется в диалоговом окне Model Setup, когда вы настраиваете переходные модели с использованием соответствующего количества входов.
xregtransient создает переходный объект модели, подходящую для использования при сдаче на хранение и удалении из тулбокса.

Успешная сдача на хранение создает некоторые выходы командной строки, и появляется рисунок с именем модели и именами переменных, отображаемыми над графиками входа и выхода оценки модели. Окончательный выход командной строки (если checkin вызывается со точки с запятой, как в предыдущем примере)

Model successfully registered for
Model-Based Calibration Toolbox software

Примечание

Вы можете увидеть ошибки, если измените файл или модель, которая задает сданную на хранение переходную модель, которую вы сейчас используете в Model Browser. См. «Восстановление после ошибок редактирования».

Использование и удаление переходных моделей

The fuelPuddle модель уже сдана на хранение для использования. Откройте Model Browser и загрузите данные, которые имеют необходимый формат для оценки этой переходной модели (два локальных входа). Входные данные времени должны быть увеличены.

Создайте план тестирования с двумя локальными факторами входа (такое же количество факторов входов, требуемых fuelPuddle модель). Теперь диалоговое окно Настройка локальной модели (Local Model Setup) предлагает следующие опции:

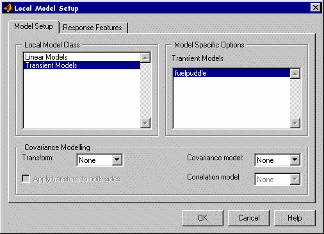
Выберите fuelpuddle модель, и нажатие кнопки OK.

О создании модели отклика с fuelPuddle как локальная модель, тулбокс соответствует двум параметрам tau и x по всем тестам.

Удаление сданных на хранение моделей. Чтобы удалить сданную на хранение модель, закройте Model Browser и введите следующую команду в командной строке:

remove(xregtransient, 'ModelName')

При перезапуске тулбокса команда удаляет сданную на хранение переходную модель.

Класс локальной модели: средняя подгонка

Можно использовать этот локальный класс модели, чтобы соответствовать той же модели всем тестам. Иногда желательно попытаться подогнать одну одноступенчатую модель к двухступенчатым данным (для примера, подгонка RBF по всей рабочей области искры, скорости, нагрузки, соотношения воздух/топливо и рециркуляции выхлопных газов). Тем не менее, все еще может быть полезным, чтобы иметь возможность исследовать подгонку модели на базисе. Для этой цели можно использовать среднее значение подгонка».

Выберите Average Fit и нажмите Setup. Откроется диалоговое окно Настройка модели (Model Setup).

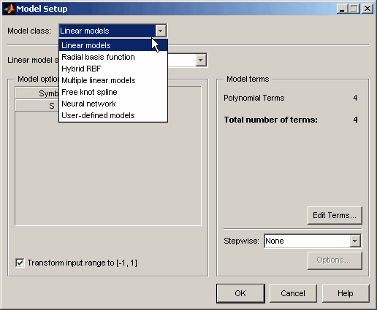
В раскрывающемся меню Model class находится список доступных моделей. Этот список содержит те же модели, которые вы найдете в глобальной настройке модели одноэтапной модели. Обратите внимание, что количество входов изменяет доступность моделей. Локальная модель с одним входом может получить доступ ко всем моделям.

Класс Average Подгонки локальная модель позволяет вам использовать любую из этих глобальных опций модели, чтобы соответствовать всем тестам. Точно так же, как глобальные модели подгоняются ко всем данным одновременно, использование средней подгонки позволяет подгонять одну и ту же модель к каждому тесту в ваших данных, вместо того, чтобы подгонять отдельную локальную модель для каждого теста.

Преимущество этого состоит в том, что вы можете использовать эти модели одного этапа для соответствия вашим данным, а также иметь возможность просматривать подгонку к каждому тесту индивидуально. Настройте свою глобальную модель с таким входом, как номер записи или фиктивная переменная. Сделайте все переменные, которые вы хотите смоделировать локальные входы. Не имеет значения, какую фиктивную переменную или тип модели вы используете для глобального входа - только там можно отличить модель Local Average Fit от одноэтапной модели. Фиктивная глобальная переменная не влияет на подгонку модели. Модель Average Fit подобрана так же, как и одноэтапная модель (одновременно во всех тестах), но основное различие заключается в том, что вы можете анализировать подгонку к каждому тесту индивидуально. Вы не можете выполнить такой анализ при подборе одноэтапных моделей.

Примечание

Двухэтапная модель не доступна с локальными моделями Average Fit, и вы не можете использовать ковариационное моделирование.

Преобразовывает

В следующем примере показаны доступные преобразования.

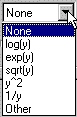
Входное преобразование может быть полезно для моделирования. Для примера, если вы пытаетесь подогнать

использование log преобразование превращает это в линейную регрессию:

Доступными преобразованиями являются логарифмические, экспоненциальные, квадратные корни,, и Other. Если вы выбираете OtherПоявится окно редактирования, в котором можно ввести функцию.

Apply transform to both sides доступна только для нелинейных моделей и преобразует и вход, и выход. Это хорошо для изменения структуры ошибки, не меняя функцию модели. Для образца журнала преобразование может сделать ошибки относительно меньшими для более высоких значений x. Где существует гетероскедастичность, как в примере Ковариации Modeling, это преобразование может иногда удалить задачу.

Ковариационное моделирование

Эта система координат видима независимо от того, какая форма локальной модели выбрана в списке.

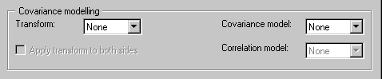
Ковариационное моделирование используется, когда существует гетероскедастичность. Это означает, что отклонение вокруг линии регрессии не является одинаковой для всех значений переменной, например, где более низкие значения скорости вращения двигателя имеют меньшую ошибку, а более высокие значения имеют большие ошибки. Если это так, точки данных на низкой скорости статистически более надежны, и им следует придавать больший вес при моделировании. Ковариационные модели используются, чтобы захватить эту структуру в ошибках.

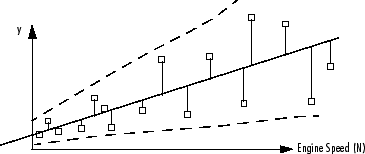
Можно подгонять модель, находя наименьшую статистику ошибок методом наименьших квадратов, когда существует гомосцедастичность (отклонение не имеет отношения к переменным). Аппроксимация методом наименьших квадратов пытается минимизировать статистику ошибок методом наименьших квадратов, где.

- ошибка, квадратная в точке i.

Когда существует гетероскедастичность, ковариационное моделирование взвешивает ошибки в пользу более статистически полезных точек (в этом примере при низкой скорости вращения двигателя N). Веса определяются с помощью функции вида

где является функцией прогнозирующей переменной (в этом примере, скорость вращения двигателя).

Существует три типа ковариационных моделей.

Степень

Они определяют веса, используя функцию вида. Подбор ковариационной модели включает оценку параметра.

Экспоненциал

Они определяют веса используя.

Смешанный

Они определяют веса используя. Существует два параметра для оценки, поэтому использование другой степени свободы. Это может быть влиятельным, когда вы выбираете модель ковариации, если используете небольшой набор данных.

Корреляционные модели

Они поддерживаются только для данных с равными интервалами в продукте Model-Based Calibration Toolbox. Когда данные коррелируются с предыдущими точками данных, ошибка также коррелируется.

Доступно три метода.

MA (1) - Метод скользящего среднего имеет вид.
AR (1) - Метод авторегрессии имеет вид.
AR (2) - Авторегрессивный метод формы является стохастическим входом,.

Документация