Функция радиального базиса имеет вид
где x - n-мерный вектор,
является n-мерным вектором, называемым центром функции радиального базиса, ||.|| обозначает евклидово расстояние и является одномерной функцией, заданной для положительных входных значений, которую мы будем называть функцией профиля.
Модель строится как линейная комбинация N радиальных базисных функций с N различными центрами. Учитывая вектор входа x, выход сети RBF является вектором активности
, заданным как
где
- вес, сопоставленный с j-ой функцией радиального базиса, с центром в 
и. 
Выход 
аппроксимирует целевое множество значений, обозначенных y.
В MBC доступны различные функции радиального базиса, каждая из которых характеризуется формой. 
Все функции радиального базиса также имеют связанный параметр ширины, 
который связан с распространением функции вокруг ее центра. Выбор поля в настройке модели обеспечивает настройку по умолчанию для ширины. Ширина по умолчанию является средним значением по центрам расстояния каждого центра до ближайшего соседа. Это эвристика, заданная в Hassoun (см. Ссылки) для Гауссов, но это только грубое руководство, которое предоставляет начальную точку для алгоритма выбора ширины.
Другой параметр, сопоставленный с радиальными функциями базиса, является параметром регуляризации. 
Этот (обычно маленький) положительный параметр используется в большинстве алгоритмов аппроксимации. Параметр
штрафует большие веса, что имеет тенденцию создавать более плавные приближения y и уменьшать склонность сети к избыточной подгонке (то есть подбирать целевые значения y хорошо, но иметь плохую прогнозирующую способность).
В следующих разделах объясняются различные параметры для радиальных функций базиса, доступных в продукте Model-Based Calibration Toolbox™, и как использовать их для моделирования.
В диалоговом окне Model Setup можно выбрать, какое ядро RBF использовать. Ядра - это типы RBF (мультиквадрический, гауссов, тонкостенных и так далее). Эти типы описаны в следующих разделах.
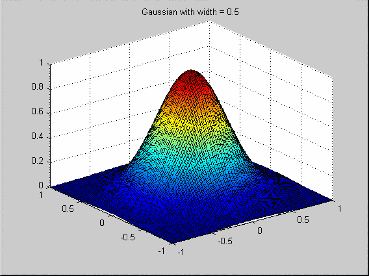
Это функция радиального базиса, наиболее часто используемая в сообществе нейронных сетей. Его функция профиля
Это приводит к функции радиального базиса
В этом случае параметр ширины аналогичен стандартному отклонению функции Гауссова.
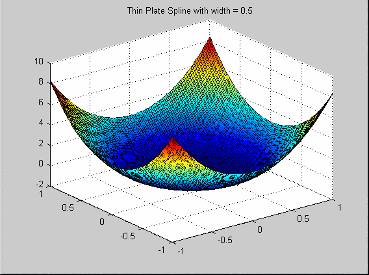
Эта функция радиального базиса является примером сглаживающего сплайна, как популяризировано Грейс Вахба (http://www.stat.wisc.edu/~wahba/). Они обычно дополнены полиномиальными терминами низкого порядка. Его функция профиля
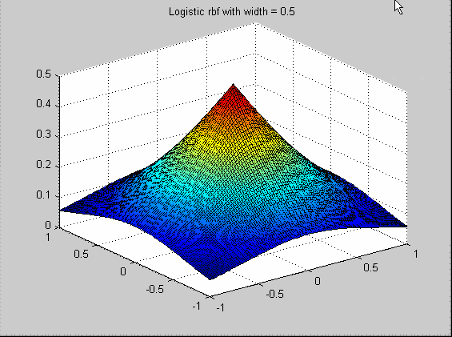
Эти радиальные функции базиса упомянуты в Hassoun (см. «Ссылки»). У них есть функция профиля
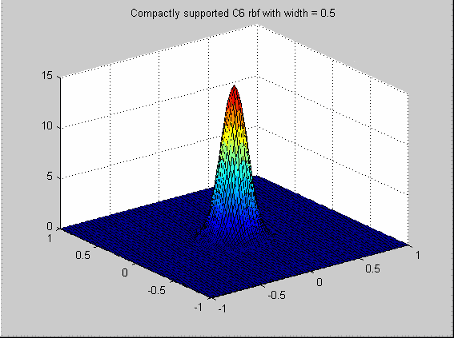
Они образуют семейство радиальных базисных функций, которые имеют кусочный полином функцию профиля и компактную поддержку [Wendland, см. Ссылки]. Представитель семейства, который нужно выбрать, зависит от размерности пространства (n), из которого получены данные, и желаемой степени непрерывности полиномов.
| Размерность | Непрерывность | Профиль |
|---|---|---|
n = 1 | 0 |
|
2 |
| |
4 |
| |
n = 3 | 0 |
|
2 | ||
4 |
| |
n = 5 | 0 |
|
2 |
| |
4 |
|
Мы использовали обозначение
для положительной части a.
Когда n четно, используется радиальная функция базиса, соответствующая размерности n + 1.
Обратите внимание, что каждая из радиальных функций базиса является ненулевой, когда r находится в [0,1]. Можно изменить поддержку, которая должна быть
путем замены r
на в предыдущей формуле. Параметр
все еще упоминается как ширина функции радиального базиса.
Подобные формулы для функций профиля существуют для n > 5 и для четной непрерывности > 4. Функции Вендланда доступны до четной непрерывности 6, и в любой пространственной размерности n.
Примечания по использованию
Лучшие свойства приближения обычно связаны с более высокой непрерывностью.
Для заданного набора данных параметр ширины для функций Вендланда должен быть больше, чем ширина, выбранная для Гауссова.
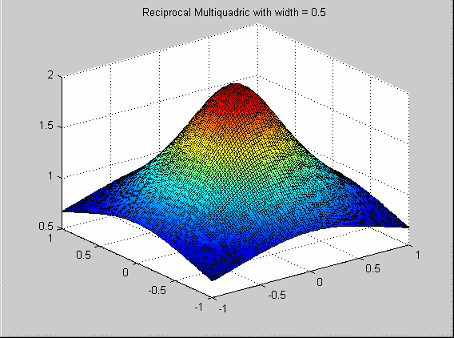
Это популярный инструмент для данного , имеющего разброса подбора кривой. У них есть функция профиля
.
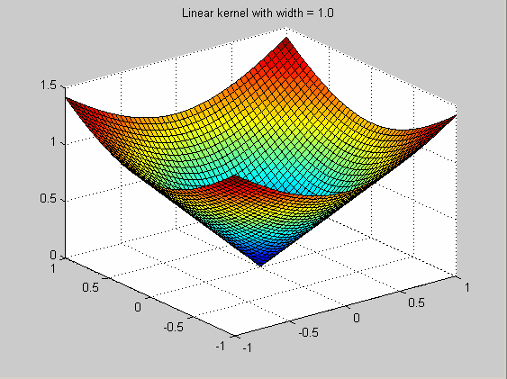
Они имеют функцию профиля
Обратите внимание, что ширина
нуля недопустима.
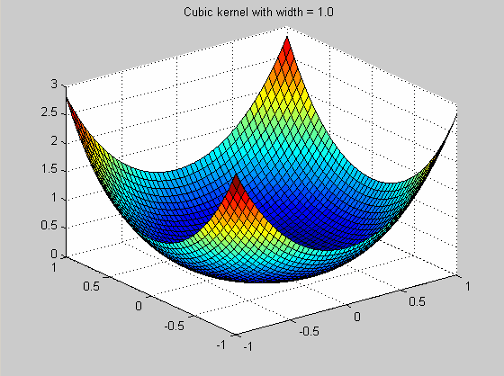
Они имеют функцию профиля.
Они имеют функцию профиля.
Существует четыре характеристики RBF, которые необходимо решить: веса, центры, ширина и. 
Каждый из них может оказать значительное влияние на качество полученной подгонки, и для каждого из них необходимо определить хорошие значения. Веса всегда определяются путем определения центров, ширины и, 
а затем решения соответствующей линейной системы уравнений. Однако задача определения хороших центров, ширины, и в
первую очередь далеко не простая, и осложняется сильными зависимостями среди параметров. Для примера оптимал
изменяется значительно по мере изменения параметра ширины. Глобальный поиск по всем возможным местоположениям центра, ширине и является
в вычислительном отношении запретительным во всех, кроме простейших ситуаций.
Чтобы попытаться бороться с этой проблемой, подгонка стандартных программ происходит на трех разных уровнях.
На самом низком уровне находятся алгоритмы, которые выбирают соответствующие центры для заданных значений ширины и. 
Центры выбираются по одному из набора кандидатов (обычно это набор точек данных или их подмножество). Поэтому получившиеся центры ранжируются в грубом порядке важности.
На среднем уровне находятся алгоритмы, которые выбирают соответствующие значения для
и центров, при заданной ширине.
На верхнем уровне находятся алгоритмы, которые стремятся найти хорошие значения для каждого из центров, ширины и. 
Эти алгоритмы верхнего уровня тестируют различные значения ширины. Для каждого значения ширины вызывается один из алгоритмов среднего уровня, который определяет хорошие центры и значения для.
Эти алгоритмы и их параметры соответствия описаны в следующих разделах:
Это основной алгоритм, как описано в Chen, Chng и Alkadhimi [См. Ссылки]. В Rols (Упорядоченные ортогональные наименьшие квадраты) центры выбираются по одному из набора кандидатов, состоящего из всех точек данных или их подмножества. Новые центры комплектуются в процедуре прямого выбора. Начиная с нулевого центра, на каждом шаге выбирается центр, который уменьшает регуляризованную ошибку больше всего. На каждом шаге регрессионная матрица X разлагается с помощью алгоритма Грама-Шмидта в продукт X = WB, где W имеет ортогональные столбцы, а B является верхним треугольным с таковыми на диагонали. Это похоже на QR-разложение. Регуляризованная ошибка задается
тем, где g = Bw и e является невязкой, заданной как. 
Минимизация регуляризованной ошибки делает суммарную квадратную ошибку
маленькой, в то же время не позволяя получить
слишком большую. Поскольку g связано с весами g = Bw, это имеет эффект держать веса под контролем и уменьшать сверхподгонку. Термин
, а не сумма квадратов весов
, используется для повышения эффективности.
Алгоритм заканчивается либо при достижении максимального количества центров, либо при добавлении новых центров значительно не уменьшается регуляризованный коэффициент ошибки (управляемый пользовательским допуском).
Подгонка параметров. Maximum number of centers - Максимальное количество центров, которые может выбрать алгоритм. Дефолт - меньшие из 25 центров или π количества точек данных. Формат следующий min(nObs/4, 25). Можно ввести значение (для примера, введите 10 создает десять центров) или отредактировать существующую формулу (для примера, (nObs/2, 25) задает половину количества точек данных или 25, в зависимости от того, какое из них меньше).
Percentage of data to be candidate centers - процент точек данных, которые должны использоваться в качестве центров-кандидатов. Это определяет подмножество точек данных, которые образуют пул для выбора центров. По умолчанию это 100%, то есть считать все точки данных возможными новыми центрами. Это может быть сокращено для ускорения времени выполнения.
Regularized error tolerance - Управляет, сколько центров выбрано перед остановкой алгоритма. Для получения дополнительной информации см. Chen, Chng и Alkadhimi [References]. Этот параметр должен быть положительным числом от 0 до 1. Большие допуски означают, что выбирается меньше центров. Значение по умолчанию является 0.0001. Если выбирается меньше максимального количества центров, и вы хотите принудительно выбрать максимальное количество, уменьшите допуск до epsilon (eps).
RedErr означает «Уменьшенная ошибка». Этот алгоритм также начинается с нулевых центров и выбирает центры в процедуре прямого выбора. Алгоритм находит (среди еще не выбранных точек данных) точку данных с самой большой невязкой и выбирает эту точку данных в качестве следующего центра. Этот процесс повторяется до тех пор, пока не будет достигнуто максимальное количество центров.
Подгонка параметров. Только имеет Number of centers.
Этот алгоритм основан на эвристике, которую вы должны поместить больше центров в область, где существуют больше изменений в невязке. Для каждой точки данных набор соседей идентифицируется как точки данных на расстоянии sqrt (nf), разделенном на максимальное количество центров, где nf - количество факторов. Вычисляются средние невязки в наборе соседей, затем количество колебаний невязки в области этой точки данных определяется как сумма квадратов различий между невязкой у каждого соседа и средними невязками соседей. Точка данных с наибольшим количеством колебаний выбирается как следующий центр.
Подгонка параметров. Почти как в Rols алгоритм, кроме Regularized error.
Этот алгоритм берёт концепцию из оптимального Проекта Экспериментов и применяет ее к задаче выбора центра в радиальных базисных функциях. Набор кандидатов центров сгенерирован латинским гиперкубом, методом, который обеспечивает квазиедиформное распределение точек. Из этого набора кандидатов n центров выбираются случайным образом. Этот набор дополнен p новыми центрами, затем этот набор n + p центров уменьшается до n путем итерационного удаления центра, который приводит к лучшей статистике PRESS (как в пошаговом). Этот процесс повторяется столько раз, сколько указано в Number of augment/reduce cycles.
CentreExchange и Tree Regression (см. «Регрессия дерева») являются единственными алгоритмами, которые разрешают использование центров, не расположенных в точках данных. Это означает, что вы не видите центры на графиках модели. The CentreExchange алгоритм может быть более гибким, чем другие алгоритмы выбора центра, которые выбирают центры, чтобы быть подмножеством точек данных; однако он значительно более длительный и не рекомендуемый для больших проблем.
Подгонка параметров. Number of centers - Количество центров, которые будут выбраны
Number of augment/reduce cycles - Количество раз, когда набор центра увеличивается, затем уменьшается
Number of centers to augment by - Сколько центров увеличить
Лямбда - параметр регуляризации.
Для заданной ширины этот алгоритм оптимизирует параметр регуляризации относительно критерия GCV (обобщенная перекрестная валидация; см. обсуждение по критерию GCV).
Начальные центры либо выбираются одним из низкоуровневых алгоритмов выбора центра, либо используется предыдущий выбор центров (см. обсуждение под Do not reselect centers параметра). Можно выбрать начальное начальное значение для
, проверяя начальное количество значений для лямбды (заданное пользователем), которые равномерно разнесены по логарифмической шкале между 10-10 и 10 и выбор с лучшим счетом GCV. Это помогает избежать падения в локальные минимумы на кривой GCV -
.
Затем параметр итератируется, чтобы попытаться минимизировать GCV с помощью формул, приведенных в разделе критерия GCV. Итерация останавливается, когда достигается максимальное количество обновлений или изменяется значение log10 (GCV) меньше, чем допуск.
Подгонка параметров. Center selection algorithm - используемый алгоритм выбора центра.
Maximum number of updates - Максимальное количество раз, когда выполняется обновление
. Значение по умолчанию является 10.
Minimum change in log10(GCV) - Допуск. Это определяет критерий остановки для итерации; 
обновление останавливается, когда различие в значении log10 (GCV) меньше допуска. Значение по умолчанию является 0.005.
Number of initial test values for lambda - Количество тестовых значений
для определения начального значения для. 
Установка этого параметра равным 0 означает, что
до сих пор используется лучший.
Do not reselect centers for new width - Этот флажок определяет, будут ли вновь выбраны центры для нового значения ширины, и после каждого обновления лямбды, или будут ли использоваться лучшие на сегодняшний день центры. Дешевле держать лучшие найденные до сих пор центры, и часто этого достаточно, но это может вызвать преждевременную сходимость к конкретному набору центров.
Display - Когда вы устанавливаете этот флажок, этот алгоритм строит графики результатов алгоритма. Начальная точка для
отмечена черным кругом. При
обновлении новые значения отображаются как красные кресты, соединенные красными линиями. Лучшее
найденное отмечено зеленой звездочкой.
Если может быть создано слишком много графиков, из-за активируемого здесь флажка Display генерируется предупреждение, и у вас есть опция остановить выполнение.
Нижняя граница 10-12 помещается на 
верхнюю границу 10.
Для заданной ширины этот алгоритм оптимизирует параметр регуляризации в Rols алгоритм относительно критерия GCV. Начальная подгонка, и центры выбираются по Rols использование предоставленного пользователем. 
Как в IterateRidge, вы выбираете начальное начальное значение для
путем тестирования начального количества начальных значений для лямбды, которые равномерно разнесены по логарифмической шкале между 10-10 и 10, и выбор с лучшим счетом GCV.
Затем итерация для улучшения GCV. Каждый раз при
обновлении повторяется процесс выбора центра. Это означает, что IterateRols намного дороже в вычислительном отношении, чем IterateRidge.
Нижняя граница 10-12 помещается на 
верхнюю границу 10.
Подгонка параметров. Center selection algorithm - используемый алгоритм выбора центра. Для IterateRols единственным доступным алгоритмом выбора центра является Rols.
Maximum number of updates - то же, что и для IterateRidge.
Minimum change in log10(GCV) - то же, что и для IterateRidge.
Number of initial test values for lambda - то же, что и для IterateRidge.
Do not reselect centers for new width - Этот флажок определяет, будут ли вновь выбраны центры для нового значения ширины или будут использоваться лучшие на сегодняшний день центры.
Display - Когда вы устанавливаете этот флажок, этот алгоритм строит графики результатов алгоритма. Начальная точка для
отмечена черным кругом.
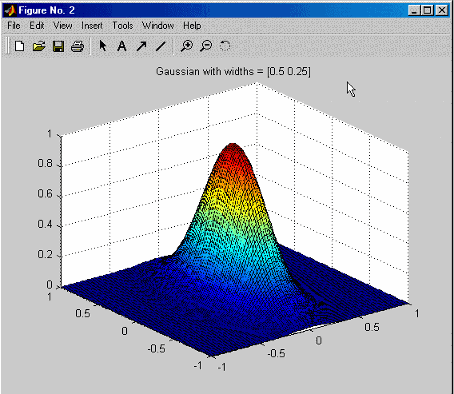
При обновлении приведенного выше рисунка новые значения отображаются как красные кресты, соединенные красными линиями. Лучшее
найденное отмечено зеленой звездочкой.
Если может быть создано слишком много графиков, из-за активируемого здесь флажка Display генерируется предупреждение, и у вас есть опция остановить выполнение.
Этот алгоритм объединяет процессы выбора центра и лямбда. Вместо ожидания, пока все центры не будут выбраны, прежде чем
будут обновлены (как и другие алгоритмы выбора лямбды), этот алгоритм предлагает возможность обновления
после выбора каждого центра. Это алгоритм прямого выбора, который, как Rols, выбирает центры на основе упорядоченного уменьшения ошибок. Критерий остановки для StepItRols на базис log10 (GCV) изменяется на меньше, чем допуск больше, чем конкретное количество раз в строке (задан в параметре Maximum number of times log10(GCV) change is minimal). Когда сложение центров остановлено, выбирается промежуточная подгонка с наименьшим log10 (GCV). Это может включать удаление некоторых центров, которые были введены поздно в алгоритме.
Подгонка параметров. Maximum number of centers - Как в Rols алгоритм.
Percentage of data to candidate centers - Как в Rols алгоритм.
Number of centers to add before updating - сколько центров выбрано перед
началом итерации.
Minimum change in log10(GCV) - Допуск. Это должно быть положительное число от 0 до 1. Значение по умолчанию является 0.005.
Maximum number of times log10(GCV) change is minimal - Управляет, сколько центров выбрано перед остановкой алгоритма. Значение по умолчанию является 5. Если значение по умолчанию не задано, выбор центра останавливается, когда значения log10 (GCV) изменяются на меньше, чем допуск пять раз подряд.
Эта стандартная программа проверяет несколько значений ширины, пробуя различные ширины. Выбирается набор пробных ширин, равномерно расположенных между заданными начальной верхней и нижней границами. Выбирается ширина с наименьшим значением log10 (GCV). Область вокруг лучшей ширины затем проверяется более подробно - это называется масштабом. В частности, новая область значений пробных ширин центрируется на лучшей ширине, найденной в предыдущей области значений, а длина интервала, из которого выбираются ширины, уменьшается до 2/5 длины интервала при предыдущем масштабе. Перед тестированием нового набора пробных ширин выбор центра обновляется, чтобы отразить лучшую ширину и
до сих пор найден. Это может означать, что расположение оптимальной ширины изменяется между масштабами из-за новых расположений в центре.
Подгонка параметров. Lambda selection algorithm - алгоритм подгонки среднего уровня, который вы тестируете с различными пробными значениями. 
Значение по умолчанию является IterateRidge.
Number of trial widths in each zoom - Количество испытаний, выполненных при каждом масштабе. Ширина теста равномерно распределена между начальной верхней и нижней границами. Значение по умолчанию является 10.
Number of zooms - Количество раз, когда вы масштабируете. Значение по умолчанию является 5.
Initial lower bound on width - нижняя граница ширины для первого масштаба. Значение по умолчанию является 0.01.
Initial upper bound on width - верхняя граница ширины для первого масштаба. Значение по умолчанию является 20.
Display - Если установлен этот флажок, строится диаграмма лист-ствол log10 (GCV) относительно ширины. Лучшая ширина отмечена зеленой звездочкой.
В WidPerDim алгоритм (Width Per Dimension), функции радиального базиса обобщены. Вместо того, чтобы иметь один параметр ширины, может использоваться разная ширина в каждом входном факторе; то есть кривые уровня эллиптические, а не округлые (или сферические, с большим количеством факторов). Базисные функции больше не являются радиально симметричными.
Это может быть особенно полезно, когда величина изменчивости значительно изменяется в каждом входном направлении. Этот алгоритм предлагает больше гибкости, чем TrialWidths, но является более в вычислительном отношении дорогим.
Можно задать Initial width в элементах управления RBF в диалоговом окне Настройка глобальной модели (Global Model Setup). Для большинства алгоритмов Initial width является одним значением. Однако для WidPerDim (доступно в раскрывающемся Width selection algorithm), можно задать вектор ширины, который будет использоваться в качестве начальных ширин.
При подаче вектора ширины должно быть столько же, сколько и количество глобальных переменных, и они должны быть в том же порядке, как указано в плане тестирования. Если вы предоставляете одну ширину, то все размерности начинаются с той же начальной ширины, но, вероятно, перейдут оттуда к вектору ширин во время подбора кривой модели.
Вычисляется оценка времени для алгоритма ширины на размерность. Это задается как количество временных модулей (так как это зависит от машины). Оценка времени более 10, но менее 100 генерирует предупреждение. Оценка времени более 100 может занять непомерно много времени (вероятно, более пяти минут на большинстве машин). У вас есть опция остановить выполнение и изменить некоторые параметры, чтобы уменьшить время запуска.
Подгонка параметров. Что касается TrialWidths алгоритм.
Существует три части алгоритма регрессии дерева для RBF:
Древовидные Создания. Алгоритм регрессии дерева создает дерево регрессии из данных и использует узлы (или панели) этого дерева, чтобы вывести центры и ширины кандидатов для RBF. Корневая панель дерева соответствует гиперкубу, который содержит все точки данных. Эта панель разделена на две дочерние панели, так что каждый дочерний элемент содержит одинаковое количество изменений, насколько это возможно. Дочерняя панель с наибольшим изменением затем разделяется подобным образом. Этот процесс продолжается до тех пор, пока не останется панелей для разделения, т.е. никакая бездетная панель не имеет больше, чем минимальное количество точек данных, или до тех пор, пока не будет достигнуто максимальное количество панелей. Каждая панель в дереве соответствует центру кандидата, и размер панели определяет ширину, которая идет с этим вектором.
Размер дочерних панелей может основываться исключительно на размере родительской панели или может определяться путем усадки дочерней панели на содержащиеся в ней данные.
После выбора Radial Basis Function в диалоговом окне Настройка глобальной модели (Global Model Setup) можно выбрать Tree Regression из раскрывающегося меню Width Selection Algorithm.
Нажмите кнопку Advanced, чтобы открыть диалоговое окно Radial Basis Functions Options (Опции радиальных функций базиса) для достижения таких настроек, как максимальное количество панелей и минимальное количество точек данных на панели. Чтобы сжать дочерние панели в соответствии с данными, установите флажок Shrink panels to data.
Алгоритм альфа-выбора. Размер ширины кандидата не берётся непосредственно из размеров панели: нам нужно масштабировать размеры панели, чтобы получить соответствующие ширины. Этот масштабный коэффициент называется альфа. Тот же масштабный коэффициент должен применяться к каждой панели в дереве и, чтобы определить оптимальное значение альфа, мы используем алгоритм альфа-выбора.
Можно выбрать параметр Specify Alpha чтобы задать точное значение альфа для использования, или можно выбрать Trial Alpha. Trial Alphaочень похож на алгоритм Пробных Ширин. Единственное различие заключается в том, что пробный альфа-алгоритм может задать, как разместить значения в поиске. Linear является таким же, как используется в пробных ширинах, но Logarithmic ищет больше значений вблизи нижней области значений.
Щелкните Advanced, чтобы открыть диалоговое окно Radial Basis Functions Options (Опции радиальных функций базиса), чтобы получить дополнительные настройки, такие как ограничения альфа-диапазона, количество масштабов и количество пробных альфа-составляющих. Здесь можно установить флажок Display, чтобы увидеть прогресс алгоритма и значения alpha trailed.
Алгоритм выбора центра. Древовидное создание генерирует центры кандидатов, а альфа-выбор генерирует ширины кандидатов для этих центров. Центр выбирает, какие из этих центров использовать.
Generic Center Selection является алгоритмом выбора центра, который ничего не знает о древовидной структуре, которая будет использоваться. В нем используются Rols, что является очень быстрым способом выбора центров и работает в данном случае, а также обычных кейсов RBF. Однако в этом случае кандидаты в центры не являются данными центров из дерева регрессии.
Tree-based center selection использует дерево регрессии. Естественно использовать дерево регрессии для выбора центров из-за того, как оно построено. В частности, панель, соответствующая корневому узлу, должна быть рассмотрена для выбора перед любым из ее дочерних элементов, так как она захватывает грубые детали, в то время как узлы в листьях дерева захватывают мелкие детали. Это то, что Tree-based center selection делает. Можно также задать максимальное количество центров.
Нажмите кнопку Advanced, чтобы открыть диалоговое окно Опции радиальных функций базиса (Radial Basis Functions Options), чтобы достичь Model selection criteria значения. Model selection criteria определяет, какая функция должна использоваться как мера того, насколько хороша модель. Это может быть BIC (Байесовский информационный критерий) или GCV (обобщенная перекрестная валидация). BIC обычно менее восприимчива к избыточному подбору кривой.
Пошаговое меню является тем же самым для всех RBF, см. «Класс глобальной модели: Функция радиального базиса».
Tree Regression и CenterExchange являются единственными алгоритмами, которые позволяют центрам, которые не расположены в точках данных. Это означает, что вы не видите центры на графиках модели.
Если вы оставляете Alpha selection algorithm по умолчанию, Trial Alpha, вы увидите диалоговое окно прогресса, когда вы кликнете OK, чтобы начать моделирование. Показан пример.
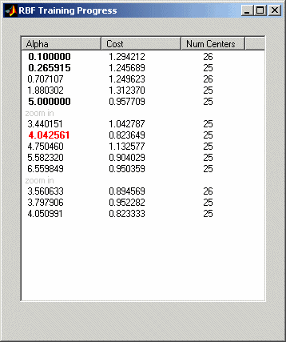
Это пример диалогового окна прогресса выполняемой модели RBF регрессии дерева. Здесь вы можете увидеть каждое пробное значение альфа с его вычисленной стоимостью и лучшим количеством центров с этим значением альфа. Альфа- значение в красном пока является лучшим. Значения Alpha больше не красные, а жирным шрифтом, являются предыдущими лучшими значениями. Затем можно уточнить модель путем изменения масштаба лучших значений для альфа и количества центров.
Ссылка: М. Орр, Дж. Халлам, К. Такэдзава, А. Мюррей, С. Ниномия, М. Ойде, Т. Леонард, «Объединение регрессионных деревьев и радиальных базисных функциональных сетей», Международный журнал нейронных систем, том 10, № 6 (2000) 453-465.
Можно использовать функцию Prune, чтобы уменьшить количество центров в радиальной функциональной сети базиса. Это помогает вам решить, сколько центров необходимо.
Для использования средства Prune:
Выберите глобальную модель RBF в дереве модели.
Либо нажмите кнопку на панели инструментов, либо выберите элемент меню Model > Utilities > Prune.
Появится диалоговое окно «Количество центров».
Графики показывают, как качество соответствия сети складывается по мере добавления большего количества RBF. Он использует тот факт, что большинство алгоритмов выбора центра имеют жадный характер, и поэтому порядок, в котором были выбраны центры, примерно отражает порядок важности базовых функций.
Критериями подгонки по умолчанию являются логарифмы PRESS, GCV, RMSE и Weighted PRESS. Дополнительные опции определяются выбранными параметрами в Сводной статистике. Взвешенный PRESS штрафует иметь больше центров, и выбор количества центров, чтобы минимизировать взвешенный PRESS, часто является хорошей опцией.
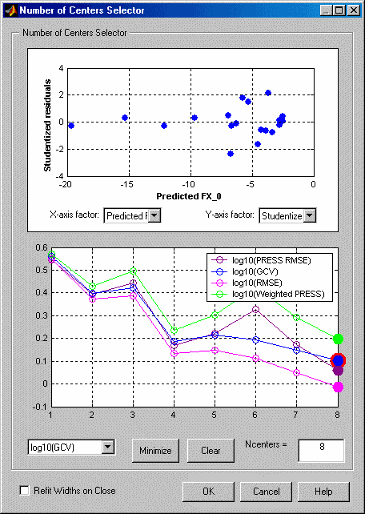
Все четыре критерия в этом типичном примере указывают один и тот же минимум в восьми центрах.
Если все графики уменьшаются, как в предыдущем примере, это предполагает, что максимальное количество центров слишком мало, и количество центров должно быть увеличено.
При нажатии кнопки Minimize выбирается количество центров, которое минимизирует критерий, выбранный в раскрывающемся меню слева. Это хорошо, если это значение также минимизирует все другие критерии. Кнопка Clear возвращается к предыдущему выбору.
Обратите внимание, что уменьшение количества центров, использующих Prune, только отменяет линейные параметры (веса RBF). Нелинейные параметры (местоположения в центре, ширина и лямбда) не корректируются. При выходе из диалогового окна можно выполнить привязку дешевой ширины, установив флажок Refit widths on close. Если сеть была значительно обрезана, необходимо использовать кнопку Update Model Fit панели инструментов. Это выполняет полное обновление всех параметров.
Предположим, что A является такой матрицей, что веса заданы
тем, где X является регрессионой. Форма A изменяется в зависимости от используемого базового алгоритма аппроксимации.
В случае обычных наименьших квадратов у нас A = X 'X.
Для регрессии гребня (с параметром регуляризации) 
A задается A = X 'X + I
Далее - алгоритм Ролса. Во время алгоритма Ролса X разлагается с помощью алгоритма Грама-Шмидта, чтобы задать X = WB, где W имеет ортогональные столбцы, а B является верхним треугольным. Соответствующая матрица А для Rols - это затем.
Матрица
называется хет-матрицей, и рычаг i-й точки данных hi задается i-м диагональным элементом H. Вся статистика, полученная из хет-матрицы, например, PRESS, исследованные невязки, доверительные интервалы и расстояние Кука, вычисляются с помощью хет-матрицы, соответствующей конкретному алгоритму аппроксимации.
Аналогично PEV, приведенный в терминах и определениях статистики тулбокса как
становится
PEV вычисляется с использованием формы A, соответствующей конкретному алгоритму аппроксимации (обычные наименьшие квадраты, хребет или ролы).
Обобщенная перекрестная валидация (GCV) является мерой качества подгонки модели к данным, которая минимизируется, когда невязки малы, но не настолько маленьки, чтобы сеть переподгоняла данные. Это легко вычислить, и сети с маленькими значениями GCV должны иметь хорошую прогностическую способность. Это связано со статистикой PRESS.
Определение GCV дано Orr (4, см. «Ссылки»).
где y - целевой вектор, N - количество наблюдений, а P - проекционная матрица, заданная I - XA-1XT. Определение A. см. в разделе «Статистика»
Важной функцией использования GCV в качестве критерия для определения оптимальной сети в наших алгоритмах аппроксимации является существование формул обновления для параметра регуляризации. 
Эти формулы обновления получаются путем дифференцирования GCV относительно
и установки результата на нуль. То есть они основаны на градиентном спуске.
Это дает общее уравнение (из Orr, 6, ссылки)
Теперь мы специализируем эти формулы на случае регрессии хребта и на алгоритме Ролса.
В Orr (4) показано, и указано в Orr (5, см. Ссылки), что для случая регрессии гребня GCV может быть записано как
где
- «эффективное количество параметров», которое задается
где NumTerms - количество членов, включенных в модель.
Для RBF 'p' является эффективным количеством параметров, то есть количеством членов минус корректировка, чтобы учесть сглаживающий эффект лямбды в алгоритме аппроксимации. Когда lambda = 0, эффективное количество параметров совпадает с количеством членов.
Формула для обновления
задается
где 
На практике предыдущие формулы не используются явно в Orr (5, см. «Ссылки»). Вместо этого делается сингулярное разложение X, и формулы переписываются в терминах собственных значений и собственных векторов матрицы XX '. Это избегает взятия обратной матрицы А, и она может использоваться, чтобы дешево вычислить GCV для многих значений
. Определение A. см. в разделе «Статистика»
В случае Rols, компоненты для формулы
вычисляются с использованием формул, приведенных в Orr [6; см. Ссылки]. Напомним, что регрессионная матрица факторизируется во время алгоритма Ролса в продукт X = WB. Пусть wj обозначает j-й столбец W, тогда мы имеем
и «эффективное количество параметров» задается как
Это эквивалентно 'p' (эффективному количеству параметров), заданному в GCV для Ridge Regression.
Формула переоценки для
задается
где дополнительно
и
Обратите внимание, что эти формулы для Rols не требуют явной инверсии A. См. Statistics для определения A.
Chen, S., Chng, E.S., Alkadhimi, Regularized Orthogonal Emergares Algorithm for Constructing Radial Basis Function Networks, Int J. Control, 1996, Vol. 64, No. 5, pp. 829-837.
Hassoun, M., Основы искусственных нейронных сетей, MIT, 1995.
Orr, M., Введение в радиальные функциональные сети базиса.
Орр, М., Оптимизация ширин функций радиального базиса.
Орр, М., Регуляризация в выборе радиальных базисных функциональных центров.
Wendland, H., Кусочные полиномы, Positive Definite и компактно поддерживаемые функции радиального базиса минимальной степени, Усовершенствований в вычислительной математике 4 (1995), pp. 389-396.
Гибридные RBF объединяют модель радиального базиса функций с более стандартными линейными моделями, такими как полиномы или гибридные сплайны. Две части складываются вместе, чтобы сформировать общую модель. Этот подход предлагает возможность сочетать априорные знания, такие как ожидание квадратичного поведения в одной из переменных, с непараметрическим характером RBF.
GUI настройки модели для гибридных RBFs имеет верхнюю кнопку Set Up , где можно задать алгоритм и опции аппроксимации. Интерфейс также имеет две вкладки, одну для задания части функции радиального базиса и одну для части линейной модели.
Это тот же алгоритм, что и используется в обычных RBF, то есть управляемый поиск наилучшего параметра ширины.
Этот алгоритм является обобщением StepItRols для RBF. Алгоритм выбирает радиальные функции базиса и линейные условия модели чередующимся образом, а не в два шага. На каждом шаге выполняется процедура прямого поиска, чтобы выбрать радиальную функцию базиса (с центром, выбранным из набора точек данных) или линейный термин модели (выбранный из тех, что заданы в панели настройки линейной модели), который больше всего уменьшает регуляризованную ошибку. Этот процесс продолжается до тех пор, пока не будет выбрано максимальное количество членов. Первые несколько членов добавляются с использованием сохраненного значения лямбды, пока Number of terms to add before updating не достигнуто. Впоследствии лямбда итератируется после добавления каждого центра для улучшения GCV.
Опции подгонки для этого алгоритма следующие:
Maximum number of terms: Максимальное количество членов, которые будут выбраны. По умолчанию это количество точек данных.
Maximum number of centers: Максимальное количество членов, которые могут быть радиальными базисными функциями. Значение по умолчанию является четвертью точек данных или 25, в зависимости от того, что меньше.
Примечание
Максимальное количество используемых членов является комбинацией максимального количества центров и количества линейных модельных членов. Оно ограничено следующим образом:
Максимальное количество используемых членов = Минимум (Maximum number of terms, Maximum number of centers + количество линейных модельных членов)
В результате этого модель может иметь больше центров, чем указано в Maximum number of centers, но всегда будет меньше членов, чем (Maximum number of centers + количество линейных членов модели). Количество возможных условий линейной модели можно просмотреть на вкладке Линейная деталь (Linear Part) диалогового окна Настройка глобальной модели (Global Model Setup) (Total number of terms).
Percentage of data to be candidate centers: Процент точек данных, доступных для выбора в качестве центров. Значение по умолчанию является 100%, когда количество точек данных является 200.
Number of terms to add before updating: Сколько терминов добавить перед началом обновления лямбды.
Minimum change in log10(GCV): допуска.
Maximum no. times log10(GCV) change is minimal: Количество шагов в строке, которое изменение в логарифмическом коде (GCV) может быть меньше, чем допуск до завершения алгоритма.
Этот алгоритм начинается с подгонки линейной модели, заданной на панели линейной модели, и затем подбирает радиальную функциональную сеть базиса к невязке. Можно задать линейные условия модели, которые будут включены обычным способом, используя селектор терминов. При необходимости можно активировать пошаговые опции. В этом случае после установки части линейной модели некоторые условия автоматически добавляются или удаляются до установки части RBF. Можно выбрать алгоритм и опции, которые используются для соответствия нелинейным параметрам RBF, нажав кнопку Set Up в опциях обучения RBF.
Определите, какие параметры оказывают наибольшее влияние на подгонку, выполнив следующие шаги:
Подбор RBF по умолчанию. Удалите все очевидные выбросы.
Получить приблизительное представление о том, сколько RBF будет необходимо. Если центр совпадает с точкой данных, он помечается пурпурной звездочкой на графике Predicted/Observed. Расположение центров можно просмотреть в графическом и табличном формате с помощью кнопки на View Centers панели инструментов. 
Если вы удалили выбросы, совпавший с центром (отмеченный звездочкой), привязайте его, нажав Update Fit на панели инструментов.
Попробуйте с несколькими ядрами. Можно изменить параметры в подгонке, нажав кнопку Set Up в диалоговом окне Выбор модели (Model Selection).
Определитесь с основным алгоритмом выбора ширины. Попробуйте с обоими TrialWidths и WidPerDim алгоритмы.
Определите, какие типы ядра выглядят наиболее обнадеживающими.
Сузите соответствующую область значений ширины для поиска.
Определитесь с алгоритмом выбора центра.
Определитесь с алгоритмом выбора лямбды.
Попробуйте изменить параметры в алгоритмах.
Если какие-либо точки кажутся возможными выбросами, попробуйте подгонять модель как с этими точками, так и без них.
Если на любом этапе вы принимаете решение об изменении, которое оказывает большое влияние (такое как удаление выбросов), то вы должны повторить предыдущие шаги, чтобы определить, повлияет ли это на выбранный вами путь.
Для получения дополнительной информации обо всех параметрах аппроксимации см. раздел Стандартных программ аппроксимации».
В Model Browser есть быстрая опция для сравнения всех различных ядер RBF и попробования множества центров.
После подбора кривой RBF по умолчанию выберите глобальную модель RBF в дереве модели.
Щелкните значок на Build Models панели инструментов.
Выберите значок RBF в появившемся диалоговом окне Создать модели (Build Models) и нажмите OK.
Откроется диалоговое окно Опции здания модели (Model Building Options). Можно задать область значений значений для максимального количества центров и нажать кнопку Model settings, чтобы изменить любые другие настройки модели. Используемые по умолчанию значения те же, что и у родительского типа модели RBF.
Можно установить флажок для Build all kernels создания моделей с заданной областью центров для каждого типа ядра в качестве выбора дочерних узлов текущей модели RBF.
Обратите внимание, что для локальных моделей это может занять много времени, так как вы создадите альтернативные модели с областью значений центров для каждого типа ядра для каждой функции отклика; После запуска построения моделей можно всегда нажать кнопку Stop, чтобы прервать процесс, если процесс занимает слишком много времени.
Щелкните Build, чтобы создать указанные модели.
Основным параметром, который необходимо настроить в порядок, чтобы получить хорошую подгонку с RBF, является максимальное количество центров. Это параметр алгоритма выбора центра и является максимальным количеством центров/RBF, которое выбрано.
Обычно максимальное количество центров - это количество фактически выбранных RBF. Однако иногда выбирается меньше RBF, потому что (регуляризованная) ошибка упала ниже допуска до достижения максимума.
Вы должны использовать ряд RBF, который значительно меньше, чем количество точек данных, в противном случае не хватает степеней свободы в ошибке, чтобы оценить прогнозирующее качество модели. То есть вы не можете сказать, полезна ли модель, если используете слишком много RBF. Мы рекомендуем верхнюю границу в 60% от отношения количества RBF к количеству точек данных. Наличие 80 центров, когда существует только 100 точек данных, может показаться хорошим значением PRESS, но, когда дело доходит до валидации, иногда может стать ясно, что данные были переоборудованы, и прогнозирующая способность не так хороша, как предполагало бы PRESS.
Одна из стратегий выбора количества RBF состоит в том, чтобы разместить больше центров, чем вы считаете нужным (скажем, 70 из 100), затем используйте кнопку панели инструментов Prune, чтобы уменьшить количество центров в модели. После обрезки сети запишите уменьшенное количество RBF. Попробуйте подгонять модель снова с максимальным количеством центров, установленным на это уменьшенное количество. Это пересчитывает значения нелинейных параметров (ширина и лямбда), чтобы быть оптимальными для уменьшенного числа RBF.
Одна из стратегий использования Stepwise состоит в том, чтобы использовать его, чтобы минимизировать PRESS как окончательную подстройку для сети, после того, как обрезка была выполнена. В то время как Prune позволяет удалить только последний введенный RBF, Stepwise позволяет вывести любой RBF.
Не фокусируйтесь исключительно на PRESS как на мере качества подгонки, особенно при больших коэффициентах RBF к точкам данных. Учитывайте также log10 (GCV).
Попробуйте оба TrialWidths и WidPerDim. Второй алгоритм предлагает большую гибкость, но является более в вычислительном отношении дорогим. Просмотрите значения ширины в каждом направлении, чтобы увидеть, есть ли существенное различие, чтобы увидеть, стоит ли фокусироваться на функциях эллиптического базиса (используйте кнопку панели инструментов View Model
).
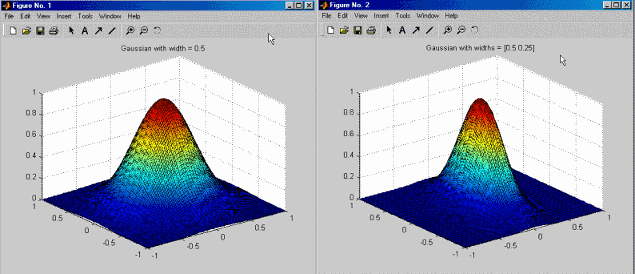
Если с различными базисными функциями ширина не сильно варьируется между размерностями, и значения PRESS/GCV не значительно улучшаются с помощью WidPerDim над TrialWidthsа затем сосредоточьтесь на TrialWidthsи просто вернемся к WidPerDim подстройку на заключительных стадиях.
Включите опцию Display в TrialWidths чтобы увидеть прогресс алгоритма. Следите за альтернативными областями в области значений ширин, которые были преждевременно проигнорированы. Выходной логарифмический параметр 10 (GCV) в конечном масштабе должен быть одинаковым для каждой из выбранных ширин; то есть выход должен быть приблизительно плоским. Если это не так, попробуйте увеличить количество масштабов.
В TrialWidths, для каждого типа RBF, попробуйте сузить начальную область значений ширин для поиска. Это может позволить уменьшить количество масштабов.
Трудно дать правила большого пальца о том, как выбрать лучший RBF, так как лучший выбор сильно зависит от данных. Лучшее руководство - попробовать все они с обоими алгоритмами верхнего уровня (TrialWidths и WidPerDim) и с разумным количеством центров сравните значения PRESS/GCV, затем сосредоточьтесь на таковых, которые выглядят наиболее обнадеживающими.
Если мультиквадрики и тонкоплитные сплайны дают плохие результаты, стоит попробовать их в сочетании с полиномами низкого порядка в качестве гибридного сплайна. Попробуйте дополнить мультиквадрики постоянным термином и тонкопластинчатыми сплайнами с линейными (порядок 1) терминами. См. Раздел «Функции гибридного радиального базиса»
Следите за проблемами обусловленности с Гауссовыми ядрами (скажем число обусловленности > 10 ^ 8).
Следите за странными результатами с функциями Вендланда, когда отношение количества параметров к количеству наблюдений высокое. Когда эти функции имеют очень маленькую ширину, каждая функция базиса способствует подгонке только в одной точке данных. Это потому, что его поддержка охватывает только одну функцию базиса, которая является его центром. Невязки будут равны нулю в каждой из точек данных, выбранных в качестве центра, и большими в других точках данных. Этот сценарий может указать хорошие значения RMSE, но прогнозирующее качество сети будет плохим.
Лямбда - параметр регуляризации.
IterateRols обновляет центры после каждого обновления лямбды. Это делает его более интенсивным в вычислительном отношении, но потенциально приводит к лучшей комбинации лямбды и центров.
StepItRols чувствителен к настройке Number of centers to add before updating. Включите опцию Display, чтобы увидеть, как log10 (GCV) уменьшается, когда количество центров складывается.
Исследуйте графики, полученные из алгоритма выбора лямбды, игнорируя предупреждение «Будет произведено чрезмерное количество графиков». Приведет ли увеличение допуска или количества начальных тестовых значений для лямбды к лучшему выбору лямбды?
По большинству задач Rols представляется наиболее эффективным.
Если выбирается меньше максимального количества центров, и необходимо принудительно выбрать максимальное число, уменьшите допуск до epsilon (eps).
CenterExchange очень дорого, и не стоит использовать это по большим задачам. В этом случае другие алгоритмы выбора центра, которые ограничивают центры в качестве подмножества точек данных, могут не предложить достаточной гибкости.
Попробуйте Stepwise после обрезки, затем обновите подгонку модели с новым максимальным количеством центров, установленным на количество членов, оставшихся после Stepwise.
Обновление модели подгонки после удаления выбросов; используйте кнопку на панели инструментов.
Перейдите к линейной панели детали и задайте полином или сплайн условия, которые вы ожидаете увидеть в модели.
Подгонка слишком многих не-RBF членов становится заметной большим значением лямбды, что указывает на то, что базовые тренды заботятся о линейной части. В этом случае вы должны сбросить начальное значение лямбды (сказать 0.001) перед следующей подгонкой.
С любой моделью можно использовать кнопку View Model на панели инструментов или View > Model Definition (или горячая клавиша CTRL + V), чтобы увидеть детали текущей модели. Откроется диалоговое окно Средство Просмотра. Здесь для любой модели RBF можно увидеть тип ядра, количество центров, ширину и параметр регуляризации.
Однако, чтобы полностью задать формулу модели RBF, необходимо также задать местоположения центров и высоту каждой функции базиса. Информация о расположении центра доступна в диалоговом окне «View Centers», а коэффициенты - в окне «Stepwise». Обратите внимание, что все эти значения указаны в кодированных модулях.
