Interior PMSM

Трехфазный синхронный двигатель с внутренними постоянными магнитами с синусоидальной противоэлектродвижущей силой

Библиотека:
Блоксет силовых агрегатов/Двигатели/Электродвигатели и инверторы
Блок управления двигателем/Электрические системы/Двигатели

Описание

Блок Interior PMSM реализует трехфазный синхронный двигатель с внутренними постоянными магнитами (PMSM) с синусоидальной противоэлектродвижущей силой. Блок использует трехфазные входные напряжения, чтобы регулировать отдельные токи фазы, позволяя контролировать крутящий момент или скорость двигателя.

По умолчанию блок устанавливает параметр Simulation type равным Continuous использование непрерывного шага расчета во время симуляции. Если вы хотите сгенерировать код для целей с двойной и одинарной точностью с фиксированным шагом, рассматривая установка параметра Discrete. Затем задайте параметр Sample Time, Ts.

На вкладке Parameters, если вы выбираете Back-emfблок реализует это уравнение, чтобы вычислить постоянную константу редактирования.

$λ_{p m} = \frac{1}{\sqrt{3}} \cdot \frac{K_{e}}{1000 P} \cdot \frac{60}{2 π}$

Моторная Конструкция

Этот рисунок показывает конструкцию мотора с одной полюсной парой на моторе.

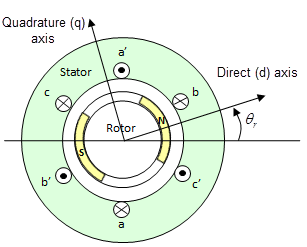
Магнитное поле двигателя от постоянных магнитов создает синусоидальную скорость изменения потока с углом двигателя.

Для соглашения о осях a-фазы и потоки постоянных магнитов выравниваются, когда угол _θr мотора равен нулю.

Трехфазная синусоидальная модель электрической системы

Блок реализует эти уравнения, выраженные в исходной системе координат потока двигателя (dq-система координат). Все величины в исходной системе координат электродвигателя относятся к статору.

$\begin{array}{l} ω_{e} = P ω_{m} \\ \frac{d}{d t} i_{d} = \frac{1}{L_{d}} v_{d} - \frac{R}{L_{d}} i_{d} + \frac{L_{q}}{L_{d}} P ω_{m} i_{q} \end{array}$

$\frac{d}{d t} i_{q} = \frac{1}{L_{q}} v_{q} - \frac{R}{L_{q}} i_{q} - \frac{L_{d}}{L_{q}} P ω_{m} i_{d} - \frac{λ_{p m} P ω_{m}}{L_{q}}$

$T_{e} = 1.5 P [λ_{p m} i_{q} + (L_{d} - L_{q}) i_{d} i_{q}]$

_Lq и _Ld индуктивности представляют отношение между индуктивностью фазы и положением двигателя из-за салиентности двигателя.

В уравнениях используются эти переменные.

_Lq, _Ld	q- и d-индуктивности (H)
R	Сопротивление обмоток статора (ом)
_iq, _id	токи q- и d-осей (A)
_vq, _vd	q- и d-осевые напряжения (V)
_ωm	Угловая механическая скорость двигателя (рад/с)
_ωe	Угловая электрическая скорость двигателя (рад/с)
_λpm	Постоянное редактирование (Wb)
_Ke	Противоэлектродвижущая сила (ЭДС) (Vpk_LL/krpm, где Vpk_LL - линейное пиковое измерение напряжения)
P	Количество пар полюсов
_Te	Электромагнитный крутящий момент (Nm)
_Θe	Электрический угол (рад)

Механическая система

Скорость вращения двигателя задается:

$\begin{matrix} \frac{d}{d t} ω_{m} = \frac{1}{J} (T_{e} - T_{f} - F ω_{m} - T_{m}) \\ \frac{d θ_{m}}{d t} = ω_{m} \end{matrix}$

В уравнениях используются эти переменные.

J	Комбинированная инерция двигателя и нагрузки (кгм ^ 2)
F	Комбинированное вязкое трение двигателя и нагрузки (Н· м/( рад/с))
_θm	Механическое угловое положение мотора (рад)
_Tm	Крутящий момент на валу мотора (Nm)
_Te	Электромагнитный крутящий момент (Nm)
_Tf	Момент трения вала мотора (Nm)
_ωm	Угловая механическая скорость двигателя (рад/с)

Учет степени

Для учета степени, блок реализует эти уравнения.

Сигнал шины			Описание	Переменная	Уравнения
`PwrInfo`	`PwrTrnsfrd` - Степень между блоками Положительные сигналы указывают на поток в блок Отрицательные сигналы указывают на выход из блока	`PwrMtr`	Механическая степень	_Pmot	$P_{m o t} = - ω_{m} T_{e}$
		`PwrBus`	Электрическая степень	_Pbus	$P_{b u s} = v_{a n} i_{a} + v_{b n} i_{b} + v_{c n} i_{c}$
	`PwrNotTrnsfrd` - Степень через контур блока, но не переданный Положительные сигналы указывают на вход Отрицательные сигналы указывают на потерю	`PwrElecLoss`	Сопротивление потери степени	_Pelec	$P_{e l e c} = - \frac{3}{2} (R_{s} i_{s d}^{2} + R_{s} i_{s q}^{2})$
		`PwrMechLoss`	Механические потери степени	_Pmech	Когда Port Configuration установлено на `Torque`: $P_{m e c h} = - (ω_{m}^{2} F + \| ω_{m} \| T_{f})$ Когда Port Configuration установлено на `Speed`: $P_{m e c h} = 0$
	`PwrStored` - Сохраненная скорость изменения энергии Положительные сигналы указывают на увеличение Отрицательные сигналы указывают на уменьшение	`PwrMtrStored`	Сохраненная степень мотора	_Pstr	$P_{s t r} = P_{b u s} + P_{m o t} + P_{e l e c} + P_{m e c h}$

В уравнениях используются эти переменные.

R s	Сопротивление статора (ом)
_ia, _ib, _ic	Фазы статора a, b и тока c (A)
_isq, _isd	Токи q- и d-осей статора (A)
_van, _vbn, _vcn	Фазы статора a, b и напряжения c (V)
_ωm	Угловая механическая скорость ротора (рад/с)
F	Комбинированный двигатель и вязкое демпфирование нагрузки (Н· м/( рад/с))
_Te	Электромагнитный крутящий момент (Nm)
_Tf	Комбинированный двигатель и крутящий момент трения нагрузки (Nm)

Амплитудно-инвариантное преобразование dq

Блок использует эти уравнения, чтобы реализовать амплитудно-инвариантное dq преобразование, чтобы убедиться, что dq и три амплитуды фазы равны.

$[\begin{matrix} v_{s d} \\ v_{s q} \end{matrix}] = \frac{2}{3} [\begin{matrix} потому что (Θ_{d a}) & потому что (Θ_{d a} - \frac{2 π}{3}) & потому что (Θ_{d a} + \frac{2 π}{3}) \\ - sin (Θ_{d a}) & - sin (Θ_{d a} - \frac{2 π}{3}) & - sin (Θ_{d a} + \frac{2 π}{3}) \end{matrix}] [\begin{matrix} v_{a} \\ v_{b} \\ v_{c} \end{matrix}]$

$[\begin{matrix} i_{a} \\ i_{b} \\ i_{c} \end{matrix}] = [\begin{matrix} потому что (Θ_{d a}) & - sin (Θ_{d a}) \\ \begin{matrix} потому что (Θ_{d a} - \frac{2 π}{3}) \\ потому что (Θ_{d a} + \frac{2 π}{3}) \end{matrix} & \begin{matrix} - sin (Θ_{d a} - \frac{2 π}{3}) \\ - sin (Θ_{d a} + \frac{2 π}{3}) \end{matrix} \end{matrix}] [\begin{matrix} i_{s d} \\ i_{s q} \end{matrix}]$

В уравнениях используются эти переменные.

_Θda	dq электрический угол статора относительно ротора a оси (рад)
_vsq, _vsd	q статора - и d - напряжения оси (V)
_isq, _isd	Токи q - и d - оси (A)
_va, _vb, _vc	Фазы напряжения статора a, b, c (V)
_ia, _ib, _ic	Токи статора фаз a, b, c (A)

Порты

Вход

расширить все

`LdTrq` - Крутящий момент на валу мотора
`scalar`

Входной крутящий момент на валу мотора, _Tm, в Н· м.

Зависимости

Чтобы создать этот порт, выберите Torque для параметра Port Configuration.

`Spd` - Скорость вала мотора
`scalar`

Скорость вращения двигателя, _ωm, в рад/с.

Зависимости

Чтобы создать этот порт, выберите Speed для параметра Port Configuration.

`PhaseVolt` - Контактные напряжения статора
`1`-by- `3` массив

Напряжения на клеммах статора, _Va, _Vb и _Vc, в В.

Зависимости

Чтобы создать этот порт, выберите Speed или Torque для параметра Port Configuration.

Выход

расширить все

`Info` - Сигнал шины
автобус

Сигнал шины содержит эти вычисления блоков.

Сигнал			Описание	Переменная	Модули
`IaStator`			Ток фазы A статора	_ia	A
`IbStator`			Ток фазы статора B	_ib	A
`IcStator`			Ток фазы статора C	_ic	A
`IdSync`			Ток прямой оси	_id	A
`IqSync`			Квадратурный ток по оси	_iq	A
`VdSync`			Напряжение прямой оси	_vd	V
`VqSync`			Квадратурная ось напряжение	_vq	V
`MtrSpd`			Угловая механическая скорость двигателя	_ωm	рад/с
`MtrPos`			Механическое угловое положение мотора	_θm	рад
`MtrTrq`			Электромагнитный крутящий момент	_Te	Н· м
`PwrInfo`	`PwrTrnsfrd`	`PwrMtr`	Механическая степень	_Pmot	W
	`PwrTrnsfrd`	`PwrBus`	Электрическая степень	_Pbus	W
	`PwrNotTrnsfrd`	`PwrElecLoss`	Сопротивление потери степени	_Pelec	W
	`PwrNotTrnsfrd`	`PwrMechLoss`	Механические потери степени	_Pmech	W
	`PwrStored`	`PwrMtrStored`	Сохраненная степень мотора	_Pstr	W

`PhaseCurr` - Фаза а, b, c тока
`1`-by- `3` массив

Фаза a, b, c тока, _ia, _ib и _ic в А.

`MtrTrq` - Крутящий момент двигателя
`scalar`

Крутящий момент двигателя, _Tmtr, в Н· м.

Зависимости

Чтобы создать этот порт, выберите Speed для параметра Mechanical input configuration.

`MtrSpd` - Скорость двигателя
`scalar`

Угловая скорость двигателя, _ωmtr, в рад/с.

Зависимости

Чтобы создать этот порт, выберите Torque для параметра Mechanical input configuration.

Параметры

расширить все

Опции блока

`Mechanical input configuration` - Выбор строения порта
`Torque` (по умолчанию) | `Speed`

В этой таблице представлены строения портов.

Строение порта	Создает Input port	Создает выходной порт
`Torque`	`LdTrq`	`MtrSpd`
`Speed`	`Spd`	`MtrTrq`

`Simulation type` - Выбор типа симуляции
`Continuous` (по умолчанию) | `Discrete`

По умолчанию блок использует непрерывный шаг расчета во время симуляции. Если вы хотите сгенерировать код для целей с одной точностью, рассмотрите установка параметра на Discrete.

Зависимости

Установка значения Simulation type Discrete создает параметр Sample Time, Ts.

`Sample Time (Ts)` - Шаг расчета для дискретного интегрирования
`scalar`

Интегрирование шага расчета для дискретной симуляции, в с.

Зависимости

Установка значения Simulation type Discrete создает параметр Sample Time, Ts.

Параметры нагрузки

`File` - Путь к параметру двигателя. «m» или «.mat» файл
`scalar`

Введите путь к параметру двигателя. «m» или. «mat» файл, который вы сохранили с помощью инструмента оценки параметра Motor Control Blockset™. Можно также нажать кнопку Browse, чтобы перемещаться и выбрать файл. «m» или «.mat», и обновить File параметр с помощью имени файла и пути. Для получения дополнительной информации, связанной с процессом оценки параметра двигателя, смотрите Оценку параметров двигателя с помощью Parameter Estimation Tool Motor Control Blockset.

Load from file - Нажмите эту кнопку, чтобы считать предполагаемые параметры двигателя из файла «.m» или «.mat» (обозначенный параметром File) и загрузить их в блок двигателей.
Save to file - Нажмите эту кнопку, чтобы считать параметры двигателя из блока двигателя и сохранить их в файл. «m» или. «mat» (с именем файла и местоположением, которое вы задаете в параметре File).

Примечание

Прежде чем вы нажмете Save to file кнопку, убедитесь, что имя целевого файла в параметре File имеет расширение «.m» или «.mat». Если вы используете любое другое расширение файла, блок выводит сообщение об ошибке.

Параметры

`Number of pole pairs (P)` - Пары полюсов
`scalar`

Пары шестов двигателей, P.

`Stator phase resistance per phase (Rs)` - Сопротивление
`scalar`

Сопротивление фазы статора на фазу, _Rs, в оме.

`Stator d-axis and q-axis inductance (Ldq)` - Индуктивность
`vector`

Статор d-составляющей и q-составляющей индуктивности, _Ld, _Lq, в Н.

`Permanent flux linkage constant (lambda_pm)` - Поток
`scalar`

Постоянная константа редактирования, _λpm, в Wb.

`Back-emf constant (Ke)` - Обратная электродвижущая сила
`scalar`

Обратная электродвижущая сила, ЭДС, _Ke, в Vpk_LL/krpm. Vpk_LL - пиковое линейное измерение напряжения.

Чтобы вычислить постоянную константу редактирования, блок реализует это уравнение.

$λ_{p m} = \frac{1}{\sqrt{3}} \cdot \frac{K_{e}}{1000 P} \cdot \frac{60}{2 π}$

`Physical inertia, viscous damping, and static friction (mechanical)` - Инерция, демпфирование, трение
`vector`

Механические свойства двигателя:

Инерция, J, в кгм ^ 2
Вязкое демпфирование, F, в Н· м/( рад/с)
Статическое трение, _Tf, в Н· м

Зависимости

Чтобы включить этот параметр, выберите Torque Параметр конфигурации.

Начальные значения

`Initial d-axis and q-axis current (idq0)` - Ток
`vector`

Начальные токи q- и d-осей, _{iq, id}, в А.

`Initial mechanical position (theta_init)` - Угол
`scalar`

Начальное угловое положение двигателя, _θm0, в рад.

`Initial mechanical speed (omega_init)` - Скорость
`scalar`

Начальная скорость вращения двигателя, _ωm0, в рад/с.

Зависимости

Чтобы включить этот параметр, выберите Torque Параметр конфигурации.

Ссылки

[1] Кундур, П. Устойчивость системы Степени и Управление. Нью-Йорк, Нью-Йорк: McGraw Hill, 1993.

[2] Андерсон, П. М. Анализ неисправных степеней. Hoboken, NJ: Wiley-IEEE Press, 1995.

Расширенные возможности

Генерация кода C/C + +
Сгенерируйте код C и C++ с помощью Coder™ Simulink ®

Введенный в R2017a

Документация

Interior PMSM

Описание

Моторная Конструкция

Трехфазная синусоидальная модель электрической системы

Механическая система

Учет степени

Амплитудно-инвариантное преобразование dq

Порты

Вход

LdTrq - Крутящий момент на валу мотора scalar

Зависимости

Spd - Скорость вала мотора scalar

Зависимости

PhaseVolt - Контактные напряжения статора 1-by- 3 массив

Зависимости

Выход

Info - Сигнал шины автобус

PhaseCurr - Фаза а, b, c тока 1-by- 3 массив

MtrTrq - Крутящий момент двигателя scalar

Зависимости

MtrSpd - Скорость двигателя scalar

Зависимости

Параметры

Mechanical input configuration - Выбор строения порта Torque (по умолчанию) | Speed

Simulation type - Выбор типа симуляции Continuous (по умолчанию) | Discrete

Зависимости

Sample Time (Ts) - Шаг расчета для дискретного интегрирования scalar

Зависимости

File - Путь к параметру двигателя. «m» или «.mat» файл scalar

Number of pole pairs (P) - Пары полюсов scalar

Stator phase resistance per phase (Rs) - Сопротивление scalar

Stator d-axis and q-axis inductance (Ldq) - Индуктивность vector

Permanent flux linkage constant (lambda_pm) - Поток scalar

Back-emf constant (Ke) - Обратная электродвижущая сила scalar

Physical inertia, viscous damping, and static friction (mechanical) - Инерция, демпфирование, трение vector

Зависимости

Initial d-axis and q-axis current (idq0) - Ток vector

Initial mechanical position (theta_init) - Угол scalar

Initial mechanical speed (omega_init) - Скорость scalar

Зависимости

Ссылки

Расширенные возможности

Генерация кода C/C + + Сгенерируйте код C и C++ с помощью Coder™ Simulink ®

Документация по Motor Control Blockset

Поддержка

`LdTrq` - Крутящий момент на валу мотора
`scalar`

`Spd` - Скорость вала мотора
`scalar`

`PhaseVolt` - Контактные напряжения статора
`1`-by- `3` массив

`Info` - Сигнал шины
автобус

`PhaseCurr` - Фаза а, b, c тока
`1`-by- `3` массив

`MtrTrq` - Крутящий момент двигателя
`scalar`

`MtrSpd` - Скорость двигателя
`scalar`

`Mechanical input configuration` - Выбор строения порта
`Torque` (по умолчанию) | `Speed`

`Simulation type` - Выбор типа симуляции
`Continuous` (по умолчанию) | `Discrete`

`Sample Time (Ts)` - Шаг расчета для дискретного интегрирования
`scalar`

`File` - Путь к параметру двигателя. «m» или «.mat» файл
`scalar`

`Number of pole pairs (P)` - Пары полюсов
`scalar`

`Stator phase resistance per phase (Rs)` - Сопротивление
`scalar`

`Stator d-axis and q-axis inductance (Ldq)` - Индуктивность
`vector`

`Permanent flux linkage constant (lambda_pm)` - Поток
`scalar`

`Back-emf constant (Ke)` - Обратная электродвижущая сила
`scalar`

`Physical inertia, viscous damping, and static friction (mechanical)` - Инерция, демпфирование, трение
`vector`

`Initial d-axis and q-axis current (idq0)` - Ток
`vector`

`Initial mechanical position (theta_init)` - Угол
`scalar`

`Initial mechanical speed (omega_init)` - Скорость
`scalar`

Генерация кода C/C + +
Сгенерируйте код C и C++ с помощью Coder™ Simulink ®