В целом решатели возвращают локальный минимум (или оптимум). Результатом может быть глобальный минимум (или оптимум), но этот результат не гарантирован.
local минимум функции является точкой, где значение функции меньше, чем в ближайших точках, но, возможно, больше, чем в удаленной точке.
Минимальным global является точка, где значение функции меньше, чем во всех других допустимых точках.
Optimization Toolbox™ решатели обычно находят локальный минимум. (Этот локальный минимум может быть глобальным минимумом.) Они находят минимум в basin of attraction начальной точки. Для получения дополнительной информации о областях притяжения смотрите Области притяжения.
Ниже приведены исключения из этого общего правила.
Задачи линейного программирования и положительно определенные квадратичные задачи программирования являются выпуклыми, с выпуклыми допустимыми областями, поэтому они имеют только одну область притяжения. В зависимости от заданных опций, linprog игнорирует любую пользовательскую начальную точку, и quadprog не требует одного, хотя иногда можно ускорить минимизацию, поставляя начальной точке.
Функции Global Optimization Toolbox, такие как simulannealbnd, попытка поиска более чем одной области притяжения.
Если вам нужен глобальный минимум, необходимо найти начальное значение для решателя в области притяжения глобального минимума.
Можно задать начальные значения для поиска глобального минимума следующими способами:
Используйте регулярную сетку начальных точек.
Используйте случайные точки, нарисованные из равномерного распределения, если все координаты задачи ограничены. Используйте точки, нарисованные из нормальных, экспоненциальных или других случайных распределений, если некоторые компоненты неограниченны. Чем меньше вы знаете о местоположении глобального минимума, тем больше должно быть распределено ваше случайное распределение. Например, нормальные распределения редко отбирают более трех стандартных отклонений от своих средств, но распределение Коши (плотность 1/( π (1 + x2))) делает сильно разрозненные выборки.
Используйте идентичные начальные точки с добавленными случайными возмущениями на каждой координате - ограниченные, нормальные, экспоненциальные или другие.
Если у вас есть лицензия Global Optimization Toolbox, используйте GlobalSearch (Global Optimization Toolbox) или MultiStart (Global Optimization Toolbox) решатели. Эти решатели автоматически генерируют случайные начальные точки в границах.
Чем больше вы знаете о возможных начальных точках, тем более сфокусирован и успешен ваш поиск будет.
Если целевая функция f (x) сглажена, вектор - ∇ f (x) указывает в направлении, где f (x) уменьшается наиболее быстро. Уравнение наискорейшего спуска, а именно
приводит к x пути (t), который достигает локального минимума с увеличениями t. Обычно начальные значения x (0), которые находятся рядом друг с другом, дают наикратчайшие пути, которые стремятся к одной и той же минимальной точке. basin of attraction для наискорейшего спуска является набором начальных значений, которые приводят к одному и тому же локальному минимуму.
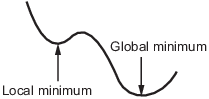
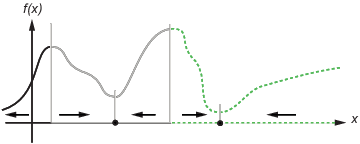
Этот рисунок показывает два одномерных минимума. Рисунок показывает различные области притяжения с различными стилями линии и указывает направления наискорейшего спуска со стрелами. Для этого и последующих рисунков черные точки представляют локальные минимумы. Каждый наикратчайший путь, начиная с точки x (0), идёт к черной точке в умывальной раковине, содержащем x (0).
Одномерные умывальные раковины
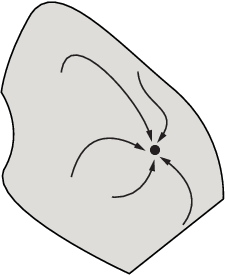
Этот рисунок показывает, как наикратчайшие пути могут быть более сложными для больших размерностей.
Один из области притяжения, показывающий наикратчайшие пути от различных начальных точек
Этот рисунок показывает еще более сложные пути и области притяжения.
Несколько областей притяжения

Ограничения могут разбить одну область притяжения на несколько частей. Например, рассмотрите минимизацию y, подверженных:
<reservedrangesplaceholder1> ≥ | x |
<reservedrangesplaceholder1> ≥ 5 – 4 (x –2)2.
Этот рисунок показывает две области притяжения с конечными точками.
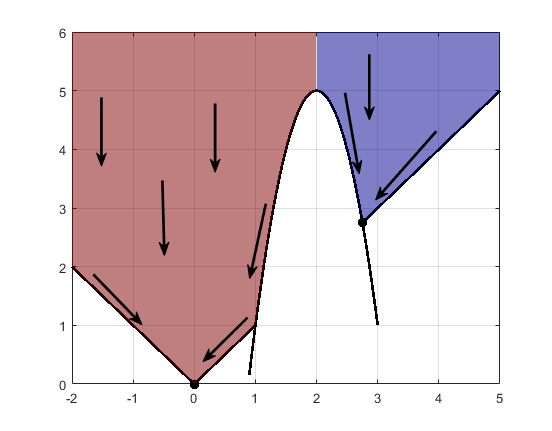
Наикратчайшие пути являются прямыми линиями до границ ограничений. От границ ограничения наикратчайших путей перемещаются вниз по контуры. Конечная точка является или (0,0) или (11/4,11/4), в зависимости от того, является ли начальное значение x выше или ниже 2 .