Двумерное полунепрерывное ограничение
Найдите значения x, которые минимизируют
f (<reservedrangesplaceholder1>) = (x 1 – 0.2)2 + (x 2 – 0.2)2 + (x 3 – 0.2)2,
где
для всех значений w 1 и w 2 по областям значений
1 <reservedrangesplaceholder0> 1 100,
1 <reservedrangesplaceholder0> 2 100,
начиная с точки x = [0,25,0,25,0,25].
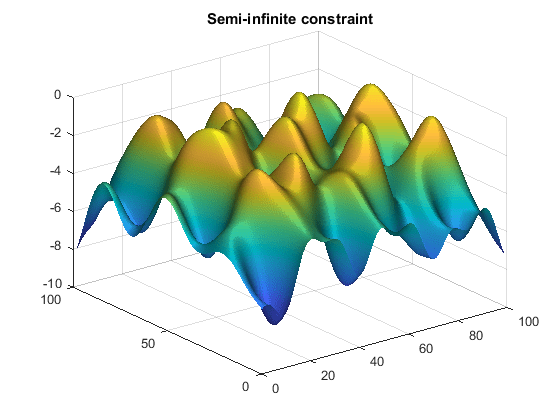
Обратите внимание, что полубесконечное ограничение является двумерным, то есть матрицей.
Сначала запишите файл, который вычисляет целевую функцию.
function f = myfun(x,s) % Objective function f = sum((x-0.2).^2);
Во-вторых, запишите файл для ограничений, называемый mycon.m. Включите код, чтобы нарисовать объемную поверхностную диаграмму полунепрерывного ограничения каждый раз mycon вызывается. Это позволяет вам увидеть, как изменяется ограничение как X минимизируется.
function [c,ceq,K1,s] = mycon(X,s)
% Initial sampling interval
if isnan(s(1,1)),
s = [2 2];
end
% Sampling set
w1x = 1:s(1,1):100;
w1y = 1:s(1,2):100;
[wx,wy] = meshgrid(w1x,w1y);
% Semi-infinite constraint
K1 = sin(wx*X(1)).*cos(wx*X(2))-1/1000*(wx-50).^2 -...
sin(wx*X(3))-X(3)+sin(wy*X(2)).*cos(wx*X(1))-...
1/1000*(wy-50).^2-sin(wy*X(3))-X(3)-1.5;
% No finite nonlinear constraints
c = []; ceq=[];
% Mesh plot
m = surf(wx,wy,K1,'edgecolor','none','facecolor','interp');
camlight headlight
title('Semi-infinite constraint')
drawnowЗатем активируйте стандартную программу оптимизации.
x0 = [0.25, 0.25, 0.25]; % Starting guess [x,fval] = fseminf(@myfun,x0,1,@mycon)
После девяти итераций решение является
x
x =
0.2523 0.1715 0.1938и значение функции в решении является
fval
fval =
0.0036Цель состояла в том, чтобы минимизировать целевое f (x) таким образом, чтобы полубесконечное ограничение, удовлетворяющее K 1 (x , w) ≤ 1,5. Оценка mycon в решении x и рассматривая максимальный элемент матрицы K1 показывает, что ограничение легко выполняется.
[c,ceq,K1] = mycon(x,[0.5,0.5]); % Sampling interval 0.5 max(max(K1)) ans = -0.0370
Этот вызов для mycon приводит к следующему графику surf, который показывает полунепрерывное ограничение в x.
