Радиолокационный кубик данных является удобным способом концептуального представления пространственно-временной обработки. Чтобы создать радиолокационный кубик данных, предположим, что предварительная обработка преобразует RF-сигналы, полученные от нескольких импульсов, через несколько элементы массива в комплексные выборки основной полосы частот. Расположите комплексные выборки основной полосы в трехмерном массиве размеров K -by- N -by - L.
K определяет длину первой (быстрой) размерности.
N определяет длину второй (пространственной) размерности.
L определяет длину третьей (медленно-временной) размерности.
Многие операции обработки радиолокационных сигналов в программном обеспечении Phased Array System Toolbox™ соответствуют обработке низкомерных подмножеств куба радиолокационных данных. Подмножеством может быть одномерный подвектор или двумерная подматрица.
Следующий рисунок показывает организацию куба радиолокационных данных в этом программном обеспечении. Последующие разделы объясняют каждую из размерностей и какой аспект пространственно-временной обработки они представляют.
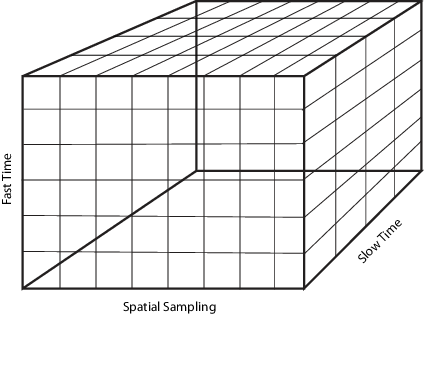
Рассмотрим K-на-1 субвектор куба радиолокационных данных вдоль оси быстрого времени на предыдущей схеме. Каждый вектор-столбец представляет набор комплексных выборок основной полосы из одного импульса в одном элементе массива, дискретизированный со скоростью. Эта частота дискретизации является самой высокой частотой дискретизации системы и приводит к fast time назначения. Выберите частоту дискретизации, , достаточно большой, чтобы избежать сглаживания. Соответствующий интервал дискретизации . Быстрая временная размерность также упоминается как размерность области значений. Быстрые интервалы выборки времени при преобразовании в расстояние с помощью скорости распространения сигнала часто упоминаются как интервалы значений области значений или затворы области значений.
Импульсное сжатие является примером операции обработки сигнала, выполняемой на быстрых временных выборках. Другой пример обработки сигналов является dechirping. В этих типах операций количество выборок в первой размерности выхода может отличаться от входа.
Рассмотрим каждую K -by L подматрицу куба радиолокационных данных. Подматрица содержит K векторов-строк с размерностью 1-by- L. Каждый из этих векторов-строк содержит комплексные выборки основной полосы частот из L различных импульсов из одного и того же интервала области значений. Для каждого из K элементов массива существует матрица L -by N. Интервал дискретизации между выборками L является pulse repetition interval (PRI). Типичные PRI намного длиннее, чем интервал быстрой дискретизации. Из-за длинных интервалов дискретизации выборки, взятые через несколько импульсов, называются slow time.
Обработка данных в медленной размерности позволяет вам оценить Допплеровский спектр в заданной области значений значений. В этом типе операции количество выборок в третьей размерности куба данных может измениться. Количество Допплеровских интервалов не обязательно равно количеству импульсов.
Критерий Найквиста применяется в равной степени к размерности медленного времени. Взаимным сигналом PRI является частота повторения импульсов (PRF). PRF дает ширину однозначного допплеровского спектра.
Фазированные решетки состоят из нескольких элементов массива. Рассмотрим каждую K -by N подматрицу куба радиолокационных данных. Каждый вектор-столбец состоит из K быстрых выборок для одного импульса, полученного в одном элементе массива. Векторы-столбцы представляют один и тот же импульс, дискретизированный между элементами N массива. Выборочные данные в N векторов-столбцов являются пространственной дискретизацией падающей формы волны. Анализ данных по элементам массива позволяет вам определить пространственное содержимое частоты каждого полученного импульса. Критерий Найквиста для пространственной дискретизации требует, чтобы элементы массива не разделялись более чем на половину длины волны несущей частоты.
В пространственных частотных операциях количество выборок во втором измерении куба данных может измениться. Количество пространственных интервалов частоты не обязательно равно количеству элементов датчика.
Beamforming является операцией пространственной фильтрации, которая объединяет данные через элементы массива, чтобы избирательно улучшать и подавлять волновые поля, падающие на массив, с конкретных направлений.
Space-time adaptive processing работает с двумерными данными угла Доплера для каждой области значений интервала. Рассмотрим K -by N -by L куба радиолокационных данных. Каждая из выборок K является данными из одной области значений. Эта область значений дискретизируется между N элементов массива и L PRI. Свертывание трехмерной матрицы в каждом интервале областей значений в N -by - L подматрицы позволяет одновременно проводить двумерный анализ угла прихода и доплеровской частоты.
Если у вас есть K сложных выборок данных основной полосы, собранных из импульсов L, полученных на N датчиках, вы можете организовать свои данные в формате, совместимом с соглашениями Phased Array System Toolbox с помощью permute. После обработки данных можно преобразовать назад в исходный формат куба данных с ipermute.
Начните с набора данных, состоящего из 200 выборок на импульс для десяти импульсов, собранных в 6 элементах датчика. Ваши данные организованы как массив 6 на 10 на 200 Matlab™. Реорганизуйте данные в систему Phased Array System Toolbox™ совместимым кубом данных.
Симулируйте эту структуру данных, используя комплексные белые Гауссовы шумовые выборки.
origdata = randn(6,10,200)+1j*randn(6,10,200);
Первая размерность origdata количество датчиков (пространственная выборка), второе измерение - количество импульсов (медленно), а третья размерность содержит быстрые выборки. Phased Array System Toolbox™ ожидает, что первая размерность будет содержать быстрые выборки, второе измерение - отдельные датчики в массиве и третья размерность - медленные выборки.
Реорганизация origdata в формате, совместимом с соглашениями о тулбоксе, введите:
newdata = permute(origdata,[3 1 2]);
The permute функция перемещает третью размерность origdata в первую размерность newdata. Первая размерность origdata становится вторым измерением newdata и второе измерение origdata становится третьей размерностью newdata. Это приводит к newdata быть организованным как быстрые выборки датчики-медленно- выборок. Теперь можно обрабатывать newdata с функциями Phased Array System Toolbox.
После обработки данных можно использовать ipermute для возврата данных в исходную структуру.
data = ipermute(newdata,[3 1 2]);
В этом случае data то же, что и origdata.