Симулируйте принятый сигнал в массиве датчиков
x = sensorsig(pos,ns,ang)pos представляет положения элементов массива, каждый из которых принят изотропным. ns указывает количество снимков симулированного сигнала. ang представляет входные направления каждого плоского волнового сигнала. Сигналы плоской волны приняты как сигналы с постоянным модулем со случайными фазами.
Симулируйте принятый сигнал в массиве и используйте данные для оценки направлений прибытия.
Примечание.Этот пример выполняется только в R2016b или более поздней версии. Если вы используете более ранний релиз, замените каждый вызов функции на эквивалентный step синтаксис. Для примера замените myObject(x) с step(myObject,x).
Создайте 8-элементный равномерный линейный массив, элементы которой разнесены на половину длины волны.
fc = 3e8; c = 3e8; lambda = c/fc; array = phased.ULA(8,lambda/2);
Симулируйте 100 снимков принятого сигнала в массиве. Предположим, что существует два сигнала, поступающих от азимута 30 ° и 60 ° соответственно. Шум белый во всех элементах массива, и ОСШ составляет 10 дБ.
x = sensorsig(getElementPosition(array)/lambda,...
100,[30 60],db2pow(-10));Используйте оценщик пространственного спектра луча, чтобы оценить направления прибытия, основываясь на моделируемых данных.
estimator = phased.BeamscanEstimator('SensorArray',array,... 'PropagationSpeed',c,'OperatingFrequency',fc,... 'DOAOutputPort',true,'NumSignals',2); [~,ang_est] = estimator(x);
Постройте график пространственного спектра, полученного в результате процесса оценки.
plotSpectrum(estimator)

На графике показаны peaks в 30 ° и 60 °.
Симулируйте прием двух некоррелированных входных сигналов, которые имеют различные уровни степени. Вектор с именем scov сохраняет уровни степени.
Создайте 8-элементный равномерный линейный массив, элементы которой разнесены на половину длины волны.
fc = 3e8; c = 3e8; lambda = c/fc; ha = phased.ULA(8,lambda/2);
Симулируйте 100 снимков принятого сигнала в массиве. Предположим, что один входящий сигнал инициируется из 30 степеней азимута и имеет степень 3 Вт. Второй входящий сигнал инициируется из 60 степеней азимута и имеет степень 1 Вт. Эти два сигнала не коррелируют друг с другом. Шум белый во всех элементах массива, и ОСШ составляет 10 дБ.
ang = [30 60];
scov = [3 1];
x = sensorsig(getElementPosition(ha)/lambda,...
100,ang,db2pow(-10),scov);Используйте оценщик пространственного спектра луча, чтобы оценить направления прибытия, основываясь на моделируемых данных.
hdoa = phased.BeamscanEstimator('SensorArray',ha,... 'PropagationSpeed',c,'OperatingFrequency',fc,... 'DOAOutputPort',true,'NumSignals',2); [~,ang_est] = step(hdoa,x);
Постройте график пространственного спектра, полученного в результате процесса оценки.
plotSpectrum(hdoa);

График показывает высокий пик в 30 степени и нижний пик в 60 степени.
Симулируйте прием трех сигналов, два из которых коррелированы.
Создайте ковариационную матрицу сигнала, в которой первый и третий из трех сигналов коррелируют друг с другом.
scov = [1 0 0.6;... 0 2 0;... 0.6 0 1];
Симулируйте прием 100 снимков трех входящих сигналов от 30 °, 40 ° и 60 ° азимута соответственно. Массив, который принимает сигналы, является однородной линейной решёткой с 8 элементами, элементы которой разнесены на половину длины волны. Шум белый во всех элементах массива, и ОСШ составляет 10 дБ.
pos = (0:7)*0.5; ns = 100; ang = [30 40 60]; ncov = db2pow(-10); x = sensorsig(pos,ns,ang,ncov,scov);
Симулируйте прием сигнала в URA. Сравните теоретическую ковариацию сигнала с ее выборочной ковариацией.
Создайте равномерный прямоугольный массив 2 на 2, элементы которой разнесены на 1/4 длины волны.
pos = 0.25 * [0 0 0 0; -1 1 -1 1; -1 -1 1 1];
Задайте степень шума независимо для каждого из четырех элементов массива. Каждая запись в ncov - степень шума элемента массива. Это положение элемента является соответствующим столбцом в pos. Предположим, что шум некоррелирован между элементами.
ncov = db2pow([-9 -10 -10 -11]);
Симулируйте 100 снимков принятого сигнала в массиве и сохраните теоретические и эмпирические ковариационные матрицы. Предположим, что один входящий сигнал инициируется из 30 ° азимута и 10 ° повышения. Второй входящий сигнал начинается от 50 ° азимута и 0 ° повышения. Сигналы имеют степень 1 Вт и являются некоррелированными.
ns = 100;
ang1 = [30; 10];
ang2 = [50; 0];
ang = [ang1, ang2];
rng default
[x,rt,r] = sensorsig(pos,ns,ang,ncov);Посмотрите величины теоретической ковариации и выборочной ковариации.
abs(rt)
ans = 4×4
2.1259 1.8181 1.9261 1.9754
1.8181 2.1000 1.5263 1.9261
1.9261 1.5263 2.1000 1.8181
1.9754 1.9261 1.8181 2.0794
abs(r)
ans = 4×4
2.2107 1.7961 2.0205 1.9813
1.7961 1.9858 1.5163 1.8384
2.0205 1.5163 2.1762 1.8072
1.9813 1.8384 1.8072 2.0000
Симулируйте прием сигнала в ULA, где шум между различными датчиками коррелирует.
Создайте однородный линейный массив с 4 элементами, элементы которой разнесены на половину длины волны.
pos = 0.5 * (0:3);
Задайте шумовую ковариационную матрицу. Значение в (k,_j_) положении в ncov матрица является ковариацией между элементами k и j массива, перечисленными в массиве.
ncov = 0.1 * [1 0.1 0 0; 0.1 1 0.1 0; 0 0.1 1 0.1; 0 0 0.1 1];
Симулируйте 100 снимков принятого сигнала в массиве. Предположим, что один входящий сигнал инициируется из азимута 60 °.
ns = 100; ang = 60; [x,rt,r] = sensorsig(pos,ns,ang,ncov);
Просмотрите теоретические и выборочные ковариационные матрицы для принимаемого сигнала.
rt,r
rt = 4×4 complex
1.1000 + 0.0000i -0.9027 - 0.4086i 0.6661 + 0.7458i -0.3033 - 0.9529i
-0.9027 + 0.4086i 1.1000 + 0.0000i -0.9027 - 0.4086i 0.6661 + 0.7458i
0.6661 - 0.7458i -0.9027 + 0.4086i 1.1000 + 0.0000i -0.9027 - 0.4086i
-0.3033 + 0.9529i 0.6661 - 0.7458i -0.9027 + 0.4086i 1.1000 + 0.0000i
r = 4×4 complex
1.1059 + 0.0000i -0.8681 - 0.4116i 0.6550 + 0.7017i -0.3151 - 0.9363i
-0.8681 + 0.4116i 1.0037 + 0.0000i -0.8458 - 0.3456i 0.6578 + 0.6750i
0.6550 - 0.7017i -0.8458 + 0.3456i 1.0260 + 0.0000i -0.8775 - 0.3753i
-0.3151 + 0.9363i 0.6578 - 0.6750i -0.8775 + 0.3753i 1.0606 + 0.0000i
pos - Положения элементов в сенсорном массивеПоложения элементов в массиве датчиков, заданные как вектор или матрица N-столбца. Значения в матрице указаны в единицах длины волны сигнала. Для примера, [0 1 2] описывает три элемента, которые разнесены на одну длину волны сигнала. N - количество элементов в массиве.
Размерности pos:
Для линейного массива вдоль оси y задайте координаты y элементов в векторе 1-by-N.
Для плоского массива в плоскости yz задайте координаты y и z элементов в столбцах матрицы 2-by-N.
Для массива произвольной формы задайте координаты x, y и z элементов в столбцах 3-by-N матрицы.
Типы данных: double
ns - Количество снимков имитируемого сигналаКоличество снимков моделируемого сигнала, заданное как положительный целочисленный скаляр. Функция возвращает это количество выборок на элемент массива.
Типы данных: double
ang - Направления входящих сигналов плоской волныНаправления входящих сигналов плоской волны, заданные в виде вектора M-столбца или матрицы в степенях. M - количество входящих сигналов.
Размерности ang:
Если ang является матрицей 2-by-M, каждый столбец задает направление. Каждый столбец имеет вид [azimuth; elevation]. Угол азимута должен быть между -180 и 180 степенями включительно. Угол возвышения должен быть от -90 до 90 степени включительно.
Если ang является вектором 1-by-M, каждый элемент задает угол азимута. В этом случае соответствующий угол возвышения принимается равным 0.
Типы данных: double
ncov - Характеристики шумаШумовые характеристики, заданные как неотрицательный скаляр, 1-by-N вектор положительных чисел или N-на-N положительно определенная матрица.
Размерности ncov:
Если ncov является скаляром, он представляет степень шума белого шума через все элементы приемного датчика в ваттах. В частности, значение 0 указывает, что шум отсутствует.
Если ncov является вектором 1-by-N, каждый элемент представляет степень шума одного из элементов датчика в ваттах. Шум некоррелирован между датчиками.
Если ncov является N-на-N матрицей, она представляет ковариации матрицу для шума во всех элементах датчика.
Типы данных: double
scov - Характеристики входящего сигналаХарактеристики входящего сигнала, заданные как положительная скалярная величина, 1-by-M вектор положительных чисел или M-на-M положительная полуопределенная матрица.
Размерности scov:
Если scov является скаляром, он представляет степень всех входящих сигналов в ваттах. В этом случае все входящие сигналы являются некоррелированными и имеют один и тот же уровень степени.
Если scov является вектором 1-by-M, каждый элемент представляет степень одного из входящих сигналов в ваттах. В этом случае все входящие сигналы являются некоррелированными друг с другом.
Если scov является матрицей M-на-M, она представляет матрицу ковариации для всех входящих сигналов. Матрица описывает корреляцию среди входящих сигналов. В этом случае scov может быть реальным или комплексным.
Типы данных: double
taper - Сужение элемента массиваСужение элемента массива, заданное как скалярный или комплексно- N вектор-столбец. Размерное N является количеством элементов массива. Если taper является скаляром, все элементы массива используют одно и то же значение. Если taper является вектором, каждая запись задает конус, примененный к соответствующему элементу массива.
Типы данных: double
Поддержка комплексного числа: Да
x - Принятый сигналns-by-N матрицаПринят сигнал в массиве, возвращен как комплексный ns-by-N матрица. Каждый столбец представляет принятый сигнал в соответствующем элементе массива. Каждая строка представляет моментальный снимок.
rt - Теоретическая ковариационная матрицаТеоретическая ковариационная матрица принимаемого сигнала, возвращенная как комплексная N-на-N матрица.
r - Выборочная ковариационная матрицаВыборочная ковариационная матрица принимаемого сигнала, возвращенная как комплексная N-на-N матрица. N - количество элементов массива. Функция выводит эту матрицу из x.
Примечание
Если вы задаете этот выходной аргумент, рассмотрите создание ns больше или равно N. В противном случае r имеет неполный ранг.
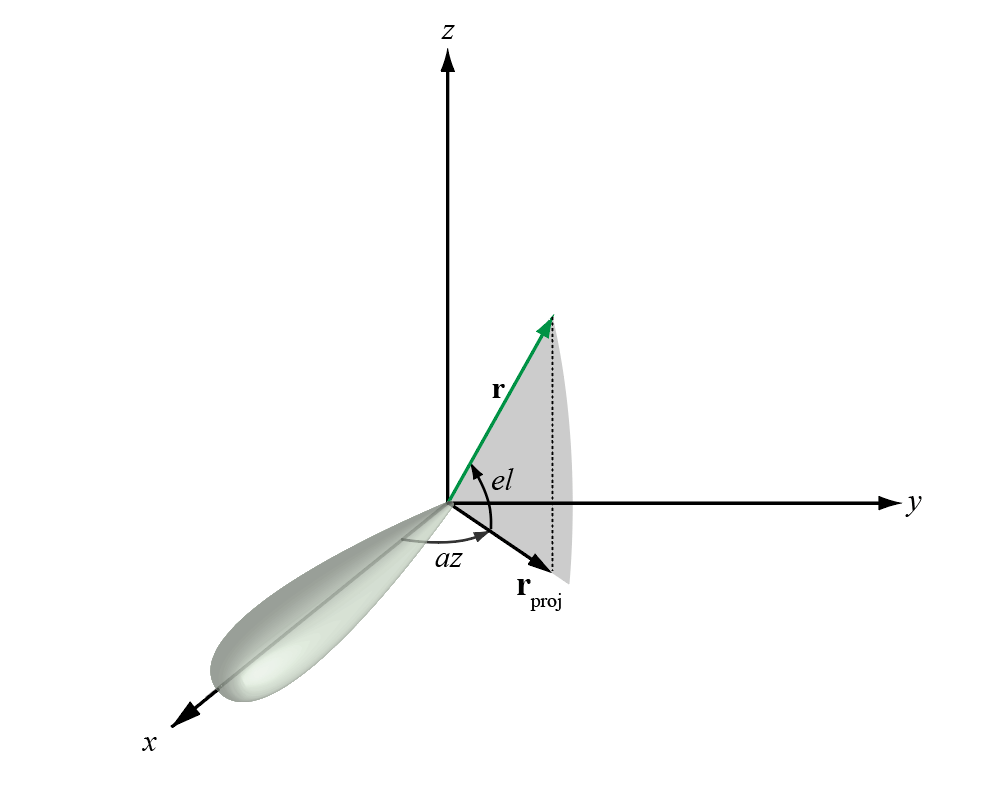
azimuth angle вектора является угол между осью x и ортогональной проекцией вектора на плоскость xy. Угол положителен в движении от оси x к оси y. Азимутальные углы лежат между -180 и 180 степенями. elevation angle является углом между вектором и его ортогональной проекцией на xy -плоск. Угол положителен при движении к положительной оси z от плоскости xy. По умолчанию направление boresight элемента или массива выровнено с положительной осью x -. Направление boresight является направлением основной лепестка элемента или массива.
Примечание
Угол возвышения иногда определяется в литературе как угол, который вектор делает с положительной осью z -. MATLAB® и Phased Array System Toolbox™ продукты не используют это определение.
Этот рисунок иллюстрирует угол азимута и угол возвышения для вектора, показанного в виде зеленой сплошной линии.
Указания и ограничения по применению:
Не поддерживает входы переменного размера.
У вас есть измененная версия этого примера. Вы хотите открыть этот пример с вашими правками?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.