Nonlinear Inductor

Индуктор с неидеальным сердечником

Библиотека:
Simscape/Электрический/Пассивный

Описание

Блок Nonlinear Inductor представляет индуктор с неидеальным сердечником. Ядро может быть неидеальным из-за его магнитных свойств и размерностей. Блок обеспечивает следующие опции параметризации:

Одна индуктивность (линейная)

Отношения между напряжением, током и потоком заданы следующими уравнениями:

$i = i_{L} + v G_{p}$

$v = N_{w} \frac{d Φ}{d t}$

$Φ = \frac{L}{N_{w}} i_{L}$

где:

v - терминальное напряжение.
i - терминальный ток.
i L является током через индуктор .
G p - паразитическая параллельная проводимость .
N w - количество витков обмотки .
Φ - магнитный поток.
L - ненасыщенная индуктивность.

Одна точка насыщения

Отношения между напряжением, током и потоком заданы следующими уравнениями:

$i = i_{L} + v G_{p}$

$v = N_{w} \frac{d Φ}{d t}$

$Φ = \frac{L}{N_{w}} i_{L} (для ненасыщенных)$

$Φ = \frac{L_{s a t}}{N_{w}} i_{L} \pm Φ_{o f f s e t} (для насыщенных)$

где:

v - терминальное напряжение.
i - терминальный ток.
i L является током через индуктор .
G p - паразитическая параллельная проводимость .
N w - количество витков обмотки .
Φ - магнитный поток.
Φ _{смещение} является смещением насыщения магнитного потока.
L - ненасыщенная индуктивность.
L _sat является насыщенной индуктивностью .

Характеристика магнитного потока от тока

Отношения между напряжением, током и потоком заданы следующими уравнениями:

$i = i_{L} + v G_{p}$

$v = N_{w} \frac{d Φ}{d t}$

$Φ = f (i_{L})$

где:

v - терминальное напряжение.
i - терминальный ток.
i L является током через индуктор .
G p - паразитическая параллельная проводимость .
N w - количество витков обмотки .
Φ - магнитный поток.

Магнитный поток определяется одномерным поиском таблицы, основанным на векторе текущих значений и векторе соответствующих значений магнитного потока, которые вы обеспечиваете. Можно создать эти векторы, используя либо отрицательные и положительные данные, либо только положительные данные. Если используются только положительные данные, вектор должен начинаться с 0, и отрицательные данные будут автоматически вычисляться вращением около (0,0).

Характеристика зависимости плотности магнитного потока от напряженности магнитного поля

Отношения между напряжением, током и потоком заданы следующими уравнениями:

$i = i_{L} + v G_{p}$

$v = N_{w} \frac{d Φ}{d t}$

$Φ = B \cdot A_{e}$

$B = f (H)$

$H = \frac{N_{w}}{l_{e}} i_{L}$

где:

v - терминальное напряжение.
i - терминальный ток.
i L является током через индуктор .
G p - паразитическая параллельная проводимость .
N w - количество витков обмотки .
Φ - магнитный поток.
B - плотность магнитного потока.
H - напряженность магнитного поля.
l e является эффективной длиной ядра .
A e является эффективной площадью поперечного сечения сердечника .

Плотность магнитного потока определяется одномерным поиском в таблице, основанным на векторе значений напряженности магнитного поля и векторе соответствующих значений плотности магнитного потока, которые вы обеспечиваете. Можно создать эти векторы, используя либо отрицательные и положительные данные, либо только положительные данные. Если используются только положительные данные, вектор должен начинаться с 0, и отрицательные данные будут автоматически вычисляться вращением около (0,0).

Характеристика зависимости плотности магнитного потока от напряженности магнитного поля с гистерезисом

Отношения между напряжением, током и потоком заданы следующими уравнениями:

$i = i_{L} + v G_{p}$

$v = N_{w} \frac{d Φ}{d t}$

$Φ = B \cdot A_{e}$

$B = μ_{0} (H + M)$

$H = \frac{N_{w}}{l_{e}} i_{L}$

где:

v - терминальное напряжение.
i - терминальный ток.
i L является током через индуктор .
G p - паразитическая параллельная проводимость .
N w - количество витков обмотки .
Φ - магнитный поток.
B - плотность магнитного потока.
μ 0 является магнитной постоянной, проницаемостью свободного пространства.
H - напряженность магнитного поля.
M - намагниченность ядра индуктора.
l e является эффективной длиной ядра .
A e является эффективной площадью поперечного сечения сердечника .

Намагниченность действует, чтобы увеличить плотность магнитного потока, и ее значение зависит как от текущего значения, так и от истории H напряженности поля. Уравнения Джайлса-Атертона [1, 2] используются для определения M в любой заданный момент времени. Рисунок ниже показывает типовой график полученной зависимости между B и H.

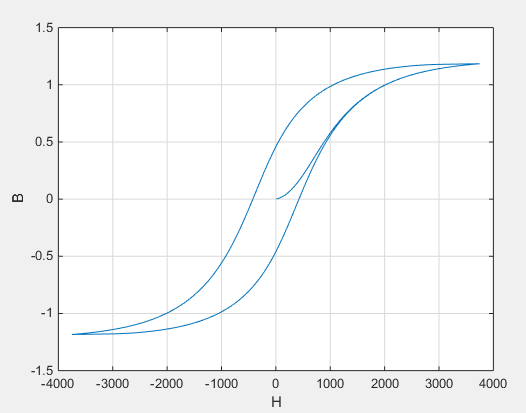
В этом случае намагниченность начинается как нуль, и, следовательно, график начинается с B = H = 0. Когда сила поля увеличивается, график стремится к положительной кривой гистерезиса; затем при изменении скорости изменения H следует отрицательная кривая гистерезиса. Различие между положительной и отрицательной кривыми обусловлено зависимостью M от истории траекторий. Физически поведение соответствует магнитным диполям в сердечнике, выравнивающимся с увеличением напряженности поля, но не полностью восстанавливающимся в их исходное положение, когда напряженность поля уменьшается.

Отправной точкой для уравнения Джайлса-Атертона является разделение эффекта намагниченности на две части, одна из которых является чисто функцией эффективной силы поля (H _eff), а другая - необратимой частью, которая зависит от прошлой истории:

$M = c M_{a n} + (1 - c) M_{i r r}$

То M термин называется безистемной намагниченностью, потому что он не проявляет гистерезиса. Это описывается следующей функцией текущего значения эффективной напряженности поля, _{H eff}:

$M_{a n} = M_{s} (\coth (\frac{H_{e f f}}{α}) - \frac{α}{H_{e f f}})$

Эта функция задает кривую насыщения с предельными значениями ± _M с и точкой насыщения, определяемой значением α, коэффициентом безистемной формы. Его можно приблизительно рассматривать как описание среднего значения двух гистеретических кривых. В блоке Nonlinear Inductor вы обеспечиваете значения для $d M_{a n} / d H_{e f f}$ при H _eff = 0 и точки [_H 1, B 1] на ангистеретической кривой B-H, и они используются для определения значений для α и M с.

Параметрический c является коэффициентом для обратимой намагниченности и диктует, какую часть поведения определяет M _и какую - необратимый термин _{M irr}. Модель Джайлса-Атертона задает необратимый термин частной производной относительно напряженности поля:

$\begin{array}{l} \frac{d M_{i r r}}{d H} = \frac{M_{a n} - M_{i r r}}{K δ - α (M_{a n} - M_{i r r})} \\ δ = {\begin{array}{l} 1 & если H \geq 0 \\ - 1 & если H < 0 \end{array} \end{array}$

Сравнение этого уравнения со стандартным дифференциальным уравнением первого порядка показывает, что, когда делаются шаги в напряженности поля, H, необратимый член, M _irr пытается отследить обратимый член _M, но с переменным отслеживающим усилением $1 / (K δ - α (M_{a n} - M_{i r r}))$ . Ошибка отслеживания действует, чтобы создать гистерезис в точках, где δ изменяет знак. Основной параметр, который формирует необратимую характеристику, K, который называется bulk coupling coefficient. Параметрический α называется inter-domain coupling factor, а также используется, чтобы задать эффективную напряженность поля, используемую при определении ангистеретической кривой:

$H_{e f f} = H + α M$

Значение α влияет на форму кривой гистерезиса, большие значения, действующие на увеличение точек пересечения оси B. Однако заметьте, что для стабильности термин $K δ - α (M_{a n} - M_{i r r})$ должен быть положительным для δ > 0 и отрицательным для δ < 0. Поэтому не все значения α допустимы, типичное максимальное значение соответствует порядку 1e-3.

Процедура нахождения приблизительных значений для коэффициентов уравнения Джайлса-Атертона

Можно определить репрезентативные параметры для коэффициентов уравнения с помощью следующей процедуры:

Задайте значение для параметра Anhysteretic B-H gradient when H is zero ( $d M_{a n} / d H_{e f f}$ когда H _eff = 0) плюс точка данных [_H 1, B 1] на ангистеретической кривой B-H. Из этих значений инициализация блока определяет значения для α и M s.
Установите параметр Coefficient for reversible magnetization, c, чтобы достичь правильного начального градиента B-H при запуске симуляции с [H B] = [0 0]. Значение c является приблизительно отношением этого начального градиента к Anhysteretic B-H gradient when H is zero. Значение c должно быть больше 0 и меньше 1.
Установите параметр Bulk coupling coefficient, K аппроксимацию величины H, когда B = 0 на положительной кривой гистерезиса.
Начните с α очень маленькой и постепенно увеличивайте, чтобы настроить значение B при пересечении H = 0 линии. Типичное значение находится в области значений от 1e-4 до 1e-3. Значения, которые являются слишком большими, вызовут тенденцию градиента кривой B-H к бесконечности, которая является нефизической и генерирует ошибку определения во время выполнения.

Иногда вам нужно выполнить итерацию на этих четырех шагах, чтобы получить хорошее соответствие с предопределенной кривой B-H.

Порты

Сохранение

расширить все

`+` - Положительный терминал
электрический

Электрический порт сопоставлен с положительным напряжением индуктора.

`-` - Отрицательный терминал
электрический

Электрический порт сопоставлен с отрицательным напряжением индуктора.

Параметры

расширить все

Главный

`Parameterized by` - Параметризация блоков
`Single saturation point` (по умолчанию) | `Single inductance (linear)` | `Magnetic flux versus current characteristic` | `Magnetic flux density versus magnetic field strength characteristic` | `Magnetic flux density versus magnetic field strength characteristic with hysteresis`

Выберите один из следующих методов параметризации блоков:

Single inductance (linear) - Обеспечить значения количества оборотов, ненасыщенной индуктивности и паразитной параллельной проводимости.
Single saturation point - Обеспечивают значения количества оборотов, ненасыщенной и насыщенной индуктивности, магнитного потока насыщения и паразитной параллельной проводимости. Это опция по умолчанию.
Magnetic flux versus current characteristic - В дополнение к количеству поворотов и паразитическому значению параллельной проводимости, предоставьте вектор тока и вектор магнитного потока, чтобы заполнить интерполяционную таблицу магнитного потока от тока.
Magnetic flux density versus magnetic field strength characteristic - В дополнение к количеству оборотов и значению паразитической параллельной проводимости, предоставьте значения эффективной длины ядра и площади поперечного сечения, а также вектора напряженности магнитного поля и вектора плотности магнитного потока, чтобы заполнить интерполяционную таблицу плотности магнитного потока от силы магнитного поля.
Magnetic flux density versus magnetic field strength characteristic with hysteresis - В дополнение к количеству поворотов и эффективной длине сердечника и площади поперечного сечения, обеспечивают значения начального ангистеретического градиента B-H кривой, плотность магнитного потока и напряженность поля в определенной точке на кривой B-H, а также коэффициент обратимой намагниченности, коэффициент объемной связи, и межобласть для определения плотности магнитного потока как функции как от текущего значения, так и от истории напряженности поля.

`Number of turns` - Общее количество оборотов
`10` (по умолчанию)

Общее количество витков проволоки, намотанной вокруг сердечника индуктора.

`Unsaturated inductance` - Ненасыщенная индуктивность
`2e-4` `H` (по умолчанию)

Значение индуктивности, используемое, когда индуктор работает в своей линейной области.

Зависимости

Этот параметр видим только, когда вы выбираете Single inductance (linear) или Single saturation point для параметра Parameterized by.

`Saturated inductance` - Насыщенная индуктивность
`1e-4` `H` (по умолчанию)

Значение индуктивности, используемое, когда индуктор работает выше своей точки насыщения.

Зависимости

Этот параметр видим только, когда вы выбираете Single saturation point для параметра Parameterized by.

`Saturation magnetic flux` - Магнитный поток насыщения
`1.3e-05` `Wb` (по умолчанию)

Значение магнитного потока, при котором индуктор насыщается.

Зависимости

Этот параметр видим только, когда вы выбираете Single saturation point для параметра Parameterized by.

`Current vector, i` - Вектор данных тока
`[0, .64, 1.28, 1.92, 2.56, 3.2]` `A` (по умолчанию)

Текущие данные, используемые для заполнения интерполяционной таблицы магнитного потока в зависимости от тока.

Зависимости

Этот параметр видим только, когда вы выбираете Magnetic flux versus current characteristic для параметра Parameterized by.

`Magnetic flux vector, phi` - Данные магнитного потока
`[0, 1.29, 2, 2.27, 2.36, 2.39] .* 1e-5` `Wb` (по умолчанию)

Данные магнитного потока, используемые для заполнения интерполяционной таблицы магнитного потока от тока.

Зависимости

Этот параметр видим только, когда вы выбираете Magnetic flux versus current characteristic для параметра Parameterized by.

`Magnetic field strength vector, H` - Вектор напряженности магнитного поля
`[0, 200, 400, 600, 800, 1000]` `A/m` (по умолчанию)

Данные по напряженности магнитного поля, используемые для заполнения интерполяционной таблицы плотности магнитного потока в зависимости от напряженности магнитного поля.

Зависимости

Этот параметр видим только, когда вы выбираете Magnetic flux density versus magnetic field strength characteristic для параметра Parameterized by.

`Magnetic flux density vector, B` - Данные плотности магнитного потока
`[0, .81, 1.25, 1.42, 1.48, 1.49]` `T` (по умолчанию)

Данные плотности магнитного потока, используемые для заполнения интерполяционной таблицы плотности магнитного потока в зависимости от напряженности магнитного поля.

Зависимости

`Effective length` - Эффективная длина ядра
`0.032` `m` (по умолчанию)

Эффективная длина ядра, то есть среднее расстояние магнитного пути.

Зависимости

Этот параметр видим только, когда вы выбираете Magnetic flux density versus magnetic field strength characteristic или Magnetic flux density versus magnetic field strength characteristic with hysteresis для параметра Parameterized by.

`Effective cross-sectional area` - Эффективная площадь поперечного сечения
`1.6e-5` `m^2` (по умолчанию)

Эффективная площадь поперечного сечения ядра, то есть средняя площадь магнитного пути.

Зависимости

`Anhysteretic B-H gradient when H is zero` - Безистеретический градиент B-H вокруг нулевой напряженности поля
`0.005` `m*T/A` (по умолчанию)

Градиент ангистеретической кривой (без гистерезиса) B-H вокруг нулевой напряженности поля. Установите его на средний градиент положительных и отрицательных кривых гистерезиса.

Зависимости

Этот параметр видим только, когда вы выбираете Magnetic flux density versus magnetic field strength characteristic with hysteresis для параметра Parameterized by.

`Flux density point on anhysteretic B-H curve` - Точка плотности потока на безистемной кривой B-H
`1.49` `T` (по умолчанию)

Задайте точку на ангистеретической кривой, задав ее значение плотности потока. Выбор точки при высокой напряженности поля, где выравниваются положительные и отрицательные кривые гистерезиса, является наиболее точнейшая опция.

Зависимости

`Corresponding field strength` - Соответствующая напряженность поля
`1000` `A/m` (по умолчанию)

Соответствующая сила поля для точки, которую вы задаете параметром Flux density point on anhysteretic B-H curve.

Зависимости

`Coefficient for reversible magnetization, c` - Коэффициент для обратимой намагниченности
`0.1` (по умолчанию)

Доля намагниченности, которая обратима. Значение должно быть больше нуля и меньше единицы.

Зависимости

`Bulk coupling coefficient, K` - Коэффициент сыпучих соединений
`200` `A/m` (по умолчанию)

Параметр Джайлса-Атертона, который в основном управляет величиной напряженности поля, при которой кривая B-H пересекает линию нулевой плотности потока.

Зависимости

`Inter-domain coupling factor, alpha` - Межобласть
`1e-4` (по умолчанию)

Параметр Джайлса-Атертона, который в основном влияет на точки, в которых кривые B-H пересекают линию напряженности нуля поля. Типичные значения находятся в области значений от 1e-4 до 1e-3.

Зависимости

`Averaging period for power logging` - Период усреднения для логгирования степени
`0` `s` (по умолчанию)

Период усреднения для расчета потерь гистерезиса. Эти потери пропорциональны площади, заключенной в траекторию B-H. Если блок возбужден на известной, фиксированной частоте, можно задать это значение на соответствующий период возбуждения, чтобы вычислить потери гистерезиса. В этом случае блок регистрирует потери гистерезиса один раз за цикл AC в переменной power_dissipated. Если вы используете решатель с фиксированным шагом, это значение должно быть целым числом, кратным размеру шага симуляции.

Если блок не возбужден на известной, фиксированной частоте, установите этот параметр равным 0. В этом случае блок устанавливает power_dissipated в нуль, и можно вычислить фактические потери гистерезиса путем постобработки записанной переменной power_instantaneous.

Зависимости

Этот параметр видим только, когда вы выбираете Magnetic flux density versus magnetic field strength characteristic with hysteresis для параметра Parameterized by на вкладке Main.

`Parasitic parallel conductance` - Паразитическая параллельная проводимость
`1e-9` `1/Ohm` (по умолчанию)

Используйте этот параметр, чтобы представлять небольшие паразитарные эффекты. Небольшая параллельная проводимость может потребоваться для симуляции некоторых топологий схем.

`Interpolation option` - Опция интерполяции
`Linear` (по умолчанию) | `Smooth`

Опция интерполяции интерполяции интерполяционной таблицы. Выберите один из следующих методов интерполяции:

Linear - Выберите эту опцию, чтобы получить лучшую эффективность.
Smooth - Выберите эту опцию, чтобы создать непрерывную кривую с непрерывными производными первого порядка.

Для получения дополнительной информации об алгоритмах интерполяции смотрите PS Lookup Table (1D) блочной страницы с описанием.

Зависимости

Этот параметр видим только, когда вы выбираете Magnetic flux versus current characteristic или Magnetic flux density versus magnetic field strength characteristic для параметра Parameterized by на вкладке Main.

Начальные условия

`Specify initial state by` - Опция спецификации начального состояния
`Current` (по умолчанию) | `Magnetic flux`

Выберите подходящую опцию спецификации начального состояния:

Current - Задайте начальное состояние индуктора начальным током через индуктор (i L). Это опция по умолчанию.
Magnetic flux - Задайте начальное состояние индуктора магнитным потоком.

Зависимости

Этот параметр не отображается, когда вы выбираете Magnetic flux density versus magnetic field strength characteristic with hysteresis для параметра Parameterized by.

`Initial current` - Начальный ток
`0` `A` (по умолчанию)

Начальное текущее значение, используемое для вычисления значения магнитного потока в начальном моменте времени. Это - ток, проходящий через индуктор. Ток компонента состоит из тока, проходящего через индуктор, и тока, проходящего через паразитную параллельную проводимость.

Зависимости

Этот параметр видим только, когда вы выбираете Current для параметра Specify initial state by.

`Initial magnetic flux` - Начальный магнитный поток
`0` `Wb` (по умолчанию)

Значение магнитного потока в начальном моменте времени.

Зависимости

Этот параметр видим только, когда вы выбираете Magnetic flux для параметра Specify initial state by.

`Initial magnetic flux density` - Начальная плотность магнитного потока
`0` `T` (по умолчанию)

Значение плотности магнитного потока в начальном моменте времени.

Зависимости

`Initial field strength` - Начальная напряженность поля
`0` `A/m` (по умолчанию)

Значение напряженности магнитного поля в начальном моменте времени.

Зависимости

Примеры моделей

Нелинейные характеристики индуктора

Сравнение нелинейного поведения индуктора для различных параметризаций. Начиная со значений фундаментальных параметров, параметры для линейных и нелинейных представлений получают. Эти параметры затем используются в модели Simscape™, и выходы симуляции сравниваются.

Индуктор с гистерезисом

Как модификация коэффициентов уравнения уравнений Джайлса-Атертона магнитного гистерезиса влияет на полученную кривую B-H. Параметры симуляции сконфигурированы, чтобы запустить четыре полных цикла AC с начальной напряженностью поля (H) и магнитной плотностью потока (B), оба установлены в нуль.

Ссылки

[1] Джайлз, Д. К. и Д. Л. Атертон. «Теория ферромагнитного гистерезиса». Журнал магнетизма и магнитных материалов. Том 61, 1986, стр. 48-60.

[2] Джайлз, Д. К. и Д. Л. Атертон. Ферромагнитный гистерезис. IEEE^® Транзакции по магнитике. Том 19, № 5, 1983, с. 2183-2184.

Расширенные возможности

Генерация кода C/C + +
Сгенерируйте код C и C++ с помощью Coder™ Simulink ®

См. также

Введенный в R2012b

Документация

Nonlinear Inductor

Описание

Одна индуктивность (линейная)

Одна точка насыщения

Характеристика магнитного потока от тока

Характеристика зависимости плотности магнитного потока от напряженности магнитного поля

Характеристика зависимости плотности магнитного потока от напряженности магнитного поля с гистерезисом

Процедура нахождения приблизительных значений для коэффициентов уравнения Джайлса-Атертона

Порты

Сохранение

+ - Положительный терминал электрический

- - Отрицательный терминал электрический

Параметры

Главный

Number of turns - Общее количество оборотов 10 (по умолчанию)

Unsaturated inductance - Ненасыщенная индуктивность 2e-4 H (по умолчанию)

Зависимости

Saturated inductance - Насыщенная индуктивность 1e-4 H (по умолчанию)

Зависимости

Saturation magnetic flux - Магнитный поток насыщения 1.3e-05 Wb (по умолчанию)

Зависимости

Current vector, i - Вектор данных тока [0, .64, 1.28, 1.92, 2.56, 3.2] A (по умолчанию)

Зависимости

Magnetic flux vector, phi - Данные магнитного потока [0, 1.29, 2, 2.27, 2.36, 2.39] .* 1e-5 Wb (по умолчанию)

Зависимости

Magnetic field strength vector, H - Вектор напряженности магнитного поля [0, 200, 400, 600, 800, 1000] A/m (по умолчанию)

Зависимости

Magnetic flux density vector, B - Данные плотности магнитного потока [0, .81, 1.25, 1.42, 1.48, 1.49] T (по умолчанию)

Зависимости

Effective length - Эффективная длина ядра 0.032 m (по умолчанию)

Зависимости

Effective cross-sectional area - Эффективная площадь поперечного сечения 1.6e-5 m^2 (по умолчанию)

Зависимости

Anhysteretic B-H gradient when H is zero - Безистеретический градиент B-H вокруг нулевой напряженности поля 0.005 m*T/A (по умолчанию)

Зависимости

Flux density point on anhysteretic B-H curve - Точка плотности потока на безистемной кривой B-H 1.49 T (по умолчанию)

Зависимости

Corresponding field strength - Соответствующая напряженность поля 1000 A/m (по умолчанию)

Зависимости

Coefficient for reversible magnetization, c - Коэффициент для обратимой намагниченности 0.1 (по умолчанию)

Зависимости

Bulk coupling coefficient, K - Коэффициент сыпучих соединений 200 A/m (по умолчанию)

Зависимости

Inter-domain coupling factor, alpha - Межобласть 1e-4 (по умолчанию)

Зависимости

Averaging period for power logging - Период усреднения для логгирования степени 0 s (по умолчанию)

Зависимости

Parasitic parallel conductance - Паразитическая параллельная проводимость 1e-9 1/Ohm (по умолчанию)

Interpolation option - Опция интерполяции Linear (по умолчанию) | Smooth

Зависимости

Начальные условия

Specify initial state by - Опция спецификации начального состояния Current (по умолчанию) | Magnetic flux

Зависимости

Initial current - Начальный ток 0 A (по умолчанию)

Зависимости

Initial magnetic flux - Начальный магнитный поток 0 Wb (по умолчанию)

Зависимости

Initial magnetic flux density - Начальная плотность магнитного потока 0 T (по умолчанию)

Зависимости

Initial field strength - Начальная напряженность поля 0 A/m (по умолчанию)

Зависимости

Примеры моделей

Нелинейные характеристики индуктора

Индуктор с гистерезисом

Ссылки

Расширенные возможности

Генерация кода C/C + + Сгенерируйте код C и C++ с помощью Coder™ Simulink ®

См. также

Simscape Electrical документация

Поддержка

`+` - Положительный терминал
электрический

`-` - Отрицательный терминал
электрический

`Number of turns` - Общее количество оборотов
`10` (по умолчанию)

`Unsaturated inductance` - Ненасыщенная индуктивность
`2e-4` `H` (по умолчанию)

`Saturated inductance` - Насыщенная индуктивность
`1e-4` `H` (по умолчанию)

`Saturation magnetic flux` - Магнитный поток насыщения
`1.3e-05` `Wb` (по умолчанию)

`Current vector, i` - Вектор данных тока
`[0, .64, 1.28, 1.92, 2.56, 3.2]` `A` (по умолчанию)

`Magnetic flux vector, phi` - Данные магнитного потока
`[0, 1.29, 2, 2.27, 2.36, 2.39] .* 1e-5` `Wb` (по умолчанию)

`Magnetic field strength vector, H` - Вектор напряженности магнитного поля
`[0, 200, 400, 600, 800, 1000]` `A/m` (по умолчанию)

`Magnetic flux density vector, B` - Данные плотности магнитного потока
`[0, .81, 1.25, 1.42, 1.48, 1.49]` `T` (по умолчанию)

`Effective length` - Эффективная длина ядра
`0.032` `m` (по умолчанию)

`Effective cross-sectional area` - Эффективная площадь поперечного сечения
`1.6e-5` `m^2` (по умолчанию)

`Anhysteretic B-H gradient when H is zero` - Безистеретический градиент B-H вокруг нулевой напряженности поля
`0.005` `m*T/A` (по умолчанию)

`Flux density point on anhysteretic B-H curve` - Точка плотности потока на безистемной кривой B-H
`1.49` `T` (по умолчанию)

`Corresponding field strength` - Соответствующая напряженность поля
`1000` `A/m` (по умолчанию)

`Coefficient for reversible magnetization, c` - Коэффициент для обратимой намагниченности
`0.1` (по умолчанию)

`Bulk coupling coefficient, K` - Коэффициент сыпучих соединений
`200` `A/m` (по умолчанию)

`Inter-domain coupling factor, alpha` - Межобласть
`1e-4` (по умолчанию)

`Averaging period for power logging` - Период усреднения для логгирования степени
`0` `s` (по умолчанию)

`Parasitic parallel conductance` - Паразитическая параллельная проводимость
`1e-9` `1/Ohm` (по умолчанию)

`Interpolation option` - Опция интерполяции
`Linear` (по умолчанию) | `Smooth`

`Specify initial state by` - Опция спецификации начального состояния
`Current` (по умолчанию) | `Magnetic flux`

`Initial current` - Начальный ток
`0` `A` (по умолчанию)

`Initial magnetic flux` - Начальный магнитный поток
`0` `Wb` (по умолчанию)

`Initial magnetic flux density` - Начальная плотность магнитного потока
`0` `T` (по умолчанию)

`Initial field strength` - Начальная напряженность поля
`0` `A/m` (по умолчанию)

Генерация кода C/C + +
Сгенерируйте код C и C++ с помощью Coder™ Simulink ®