Piezo Bender

Пьезоэлектрический биморфный брус прямоугольного сечения

Библиотека:
Simscape/Электрический/Электромеханический/Мехатронный Приводы

Описание

Блок Piezo Bender моделирует пьезоэлементный пучок биморфа прямоугольного сечения.

Пьезогенератор является пьезоэлектрическим устройством, которое изгибается, когда вы прикладываете электрический потенциал между его пластинами. И наоборот, когда пьезогибатель изгибается, он генерирует электрический потенциал.

Пьезоизгиб содержит различные прямоугольные слои пьезоэлектрического материала с поляризацией перпендикулярной стеку. Эта поляризация чередуется в каждом слое.

Уравнения

Этот рисунок показывает декартовую систему координат

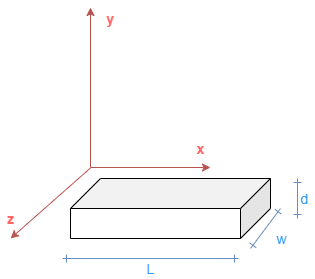
где:

L - длина балки.
w - ширина луча.
d - толщина балки.

Это конститутивные уравнения для пьезоэлектрического материала в композиции стресс-заряда,

T = [c] S - {[e]}^{T} E

(1)

D = [e] S - [ϵ^{S}] E

(2)

где:

T - поле напряжения.
[c] - тензор податливости.
S - поле деформации.
[e] - тензор коэффициента пьезометрического напряжения.
E - электрическое поле.
D - поле электрического смещения.
[ϵ^S] - тензор диэлектрической проницаемости при постоянной или нулевой деформации.

Чтобы смоделировать гибкость, блок использует конечноэлементные лучевые уравнения Эйлера-Бернулли. Перемещение и вращение каждого поперечного сечения балки в функции оси x определяют кинематику балки.

Этот блок рассматривает только силы, приложенные в y направлении, и пьезоэлектрический материал поляризован, чтобы сгибаться только в x-y плоскости. По этой причине, чтобы описать кинематику, необходимо только задать вертикальное перемещение в y направлении центра тяжести каждого поперечного сечения, y(x) и вращение вокруг оси z каждого поперечного сечения, _φz(x).

Из предыдущих предположений поле деформации в луче Эйлера-Бернулли, подлежащем изгибу, равно:

S_{x x} (x, y) = - y \frac{d φ_{z}}{d x} (x) .

(3)

Потому что электрическое поле постоянно между положительной и отрицательной пластинами, $E_{y} = \frac{v}{d}$ блок подставляет уравнение 3 в уравнение 1:

$T_{x x} (x, y) = - E y \frac{d φ_{z}}{d x} (x) - e_{31} \frac{v}{d} .$

В этом уравнении _{E = c11} является модулем Янга материала и _e31 является (3,1) пьезоэлектрическим коэффициентом связи напряжение-заряд, $σ_{x x} = - e_{31} E_{y}$ .

Это уравнение задает изгибающий момент из поля напряжения:

$M_{z} (x) = - \iint y T_{x x} (x, y) d S = \iint E y^{2} \frac{d φ_{z}}{d x} (x) + e_{31} \frac{v}{d} y d S .$

Потому что поляризация материала для $y = [- \frac{d}{2}, 0]$ является противоположным, чем поляризация для $y = [0, \frac{d}{2}]$ (3,1) пьезоэлектрический коэффициент связи напряжение-заряд изменяет знак, и изгибающий момент определяется как

$M_{z} (x) = \frac{E}{12} w d^{3} \frac{d φ_{z}}{d x} (x) + w d e_{31} v = E I \frac{d φ_{z}}{d x} (x) + w d e_{31} v,$

где $I = \frac{1}{12} w d^{3}$ - второй момент площади прямоугольного поперечного сечения.

В этом уравнении первый член является классическим уравнением луча, подлежащего изгибу, а второй член является электромеханическим соединением из-за наличия напряжения на пьезоэлектрическом материале. Это напряжение создает равномерный электрический изгибающий момент, нагруженный вдоль луча.

Затем блок подставляет уравнение 3 в уравнение 2:

$D_{y} (x, y) = - e_{31} y \frac{d φ_{z}}{d x} (x) + \frac{ϵ v}{d} .$

Электрический заряд внутри объема равен интегралу Гаусса электрического перемещения:

$d q (x) = ∯ D_{y} d S = e_{31} d w d x \frac{d φ_{z}}{d x} = e_{31} d w d φ_{z} .$

Затем это уравнение определяет заряд, накопленный между двумя участками луча из-за пьезоэлектрического эффекта:

$q = e_{31} d w (φ_{z} (x_{2}) - φ_{z} (x_{1})) .$

Наконец, с механической точки зрения можно смоделировать пьезогенератор как балку Эйлера-Бернулли, нагруженную равномерным крутящим моментом, пропорциональным напряжению:

$M_{z} (x) = E I \frac{d φ_{z}}{d x} (x) + w d e_{31} v$

С электрической точки зрения можно смоделировать пьезогенератор как конденсатор с источником заряда, пропорциональным углу изгиба:

$q = e_{31} d w (φ_{z R} - φ_{z C}) + \frac{ϵ w l}{d} v .$

Формулировка конечного элемента

Чтобы дискретизировать и решить уравнения Эйлера-Бернулли с пьезоэлектрическим связыванием, Piezo Bender блок использует метод Конечного Элемента.

Блок дискретизирует пьезогенерирующую балку на ряд срезов в направлении длины с той же шириной, w и толщиной, d. Длина каждого элемента равна общей длине балки, разделенной на количество элементов, $l = \frac{L}{N_{e l e m e n t s}}$ .

Эта матрица жесткости конечного элемента балки Эйлера-Бернулли задает отношение между вертикальным перемещением и углом поворота каждого конца балочного элемента и соответствующими силами и моментами, обусловленными упругостью балки:

$[\begin{matrix} F_{C} \\ T_{C} \\ F_{R} \\ T_{R} \end{matrix}] = [\begin{matrix} \frac{12 E I}{l^{3}} & \frac{6 E I}{l^{2}} & - \frac{12 E I}{l^{3}} & \frac{6 E I}{l^{2}} \\ \frac{6 E I}{l^{2}} & \frac{4 E I}{l} & - \frac{6 E I}{l^{2}} & \frac{2 E I}{l} \\ - \frac{12 E I}{l^{3}} & - \frac{6 E I}{l^{2}} & \frac{12 E I}{l^{3}} & - \frac{6 E I}{l^{2}} \\ \frac{6 E I}{l^{2}} & \frac{2 E I}{l} & - \frac{6 E I}{l^{2}} & \frac{4 E I}{l} \end{matrix}] [\begin{matrix} y_{C} \\ φ_{C} \\ y_{R} \\ φ_{R} \end{matrix}] .$

Затем, чтобы получить уравнения для пьезогенерирующего элемента луча, добавьте условия связи и большую матрицу для инерции:

$\frac{ρ l w d}{420} [\begin{matrix} 156 & 22 l & 54 & - 13 l \\ 22 l & 4 l^{2} & 13 l & - 3 l^{2} \\ 54 & 13 l & 156 & - 22 l \\ - 13 l & - 3 l^{2} & - 22 l & 4 l^{2} \end{matrix}] [\begin{matrix} \frac{d^{2} y_{C}}{d t^{2}} \\ \frac{d^{2} φ_{C}}{d t^{2}} \\ \frac{d^{2} y_{R}}{d t^{2}} \\ \frac{d^{2} φ_{R}}{d t^{2}} \\ 0 \end{matrix}] + [\begin{matrix} \frac{12 E I}{l^{3}} & \frac{6 E I}{l^{2}} & - \frac{12 E I}{l^{3}} & \frac{6 E I}{l^{2}} & 0 \\ \frac{6 E I}{l^{2}} & \frac{4 E I}{l} & - \frac{6 E I}{l^{2}} & \frac{2 E I}{l} & e_{31} w d \\ - \frac{12 E I}{l^{3}} & - \frac{6 E I}{l^{2}} & \frac{12 E I}{l^{3}} & - \frac{6 E I}{l^{2}} & 0 \\ \frac{6 E I}{l^{2}} & \frac{2 E I}{l} & - \frac{6 E I}{l^{2}} & \frac{4 E I}{l} & - e_{31} w d \\ 0 & - e_{31} w d & 0 & e_{31} w d & \frac{ϵ w l}{d} \end{matrix}] [\begin{matrix} y_{C} \\ φ_{C} \\ y_{R} \\ φ_{R} \\ v \end{matrix}] = [\begin{matrix} F_{C} \\ T_{C} \\ F_{R} \\ T_{R} \\ q \end{matrix}] .$

Наконец, это уравнение для пьезоизгибающего элемента балки с демпфированием:

$\frac{ρ l w d}{420} [\begin{matrix} 156 & 22 l & 54 & - 13 l \\ 22 l & 4 l^{2} & 13 l & - 3 l^{2} \\ 54 & 13 l & 156 & - 22 l \\ - 13 l & - 3 l^{2} & - 22 l & 4 l^{2} \end{matrix}] [\begin{matrix} \frac{d^{2} y_{C}}{d t^{2}} \\ \frac{d^{2} φ_{C}}{d t^{2}} \\ \frac{d^{2} y_{R}}{d t^{2}} \\ \frac{d^{2} φ_{R}}{d t^{2}} \\ 0 \end{matrix}] + [\begin{matrix} [B] & \dots & 0 \\ ⋮ & ⋱ & ⋮ \\ 0 & \dots & 0 \end{matrix}] [\begin{matrix} \frac{d y_{C}}{d t} \\ \frac{d φ_{C}}{d t} \\ \frac{d y_{R}}{d t} \\ \frac{d φ_{R}}{d t} \\ 0 \end{matrix}] + [\begin{matrix} \frac{12 E I}{l^{3}} & \frac{6 E I}{l^{2}} & - \frac{12 E I}{l^{3}} & \frac{6 E I}{l^{2}} & 0 \\ \frac{6 E I}{l^{2}} & \frac{4 E I}{l} & - \frac{6 E I}{l^{2}} & \frac{2 E I}{l} & e_{31} w d \\ - \frac{12 E I}{l^{3}} & - \frac{6 E I}{l^{2}} & \frac{12 E I}{l^{3}} & - \frac{6 E I}{l^{2}} & 0 \\ \frac{6 E I}{l^{2}} & \frac{2 E I}{l} & - \frac{6 E I}{l^{2}} & \frac{4 E I}{l} & - e_{31} w d \\ 0 & - e_{31} w d & 0 & e_{31} w d & \frac{ϵ w l}{d} \end{matrix}] [\begin{matrix} y_{C} \\ φ_{C} \\ y_{R} \\ φ_{R} \\ v \end{matrix}] = [\begin{matrix} F_{C} \\ T_{C} \\ F_{R} \\ T_{R} \\ q \end{matrix}]$

где:

l - длина элемента.
w - ширина элемента.
d - толщина элемента.
$I = \frac{1}{12} w t^{3}$ - второй момент площади.
E - модуль Янга.
m = ρlwd - масса элемента, где ρ - плотность массы.
_e31 - (3,1) пьезоэлектрический коэффициент связи напряжение-заряд, $σ_{x x} = - e_{31} E_{y}$ .
ε - электрическая диэлектрическая проницаемость.
$B = b_{k} K + b_{m} M$ - матрица демпфирования.
_bm - коэффициент Релея демпфирования, пропорциональный массе.
_bk - коэффициент Релея демпфирования, пропорциональный жесткости.
$K = [\begin{matrix} \frac{12 E I}{l^{3}} & \frac{6 E I}{l^{2}} & - \frac{12 E I}{l^{3}} & \frac{6 E I}{l^{2}} \\ \frac{6 E I}{l^{2}} & \frac{4 E I}{l} & - \frac{6 E I}{l^{2}} & \frac{2 E I}{l} \\ - \frac{12 E I}{l^{3}} & - \frac{6 E I}{l^{2}} & \frac{12 E I}{l^{3}} & - \frac{6 E I}{l^{2}} \\ \frac{6 E I}{l^{2}} & \frac{2 E I}{l} & - \frac{6 E I}{l^{2}} & \frac{4 E I}{l} \end{matrix}]$ - матрица конечного элемента жесткости.
$M = \frac{ρ l w d}{420} [\begin{matrix} 156 & 22 l & 54 & - 13 l \\ 22 l & 4 l^{2} & 13 l & - 3 l^{2} \\ 54 & 13 l & 156 & - 22 l \\ - 13 l & - 3 l^{2} & - 22 l & 4 l^{2} \end{matrix}]$ - большая матрица.
_yC - отклонение вдоль y оси левого конца элемента .
_yR - отклонение вдоль оси y правого конца элемента .
_φC - поворот вокруг z оси левого конца элемента .
_φR - поворот вокруг z оси правого конца элемента .
_FC - сила вдоль оси y левого конца элемента .
_FR - сила вдоль оси y правого конца элемента .
_TC - крутящий момент в z -оси левого конца элемента .
_TR - крутящий момент в z -оси правого конца элемента .
v - напряжение на верхнем и нижнем электродах.
q - накопленный заряд между электродами и пьезоэлектрическим материалом.

Параметризация таблицы данных

Таблица данных пьезобендера обычно предоставляет следующие данные:

Размерности (l, w, d)
Масса, m
Номинальное напряжение, _vrated
Свободный прогиб при номинальном напряжении, _yfree
Блокирующая сила при номинальном напряжении, _Fblock
Емкость, _Cpiezo
Первая резонансная частота, _f1

Можно вычислить основные параметры материала пьезогенератора с помощью параметров таблицы данных.

Во-первых, блок решает зависимости отклонения силы напряжения из установившихся уравнений без приложенного крутящего момента и без зажима строения:

$[\begin{matrix} \frac{12 E I}{l^{3}} & - \frac{6 E I}{l^{2}} & 0 \\ - \frac{6 E I}{l^{2}} & \frac{4 E I}{l} & - e_{31} w d \\ 0 & e_{31} w d & \frac{ε w l}{d} \end{matrix}] [\begin{matrix} y_{R} \\ φ_{R} \\ v \end{matrix}] = [\begin{matrix} F_{R} \\ 0 \\ q \end{matrix}] .$

Эти уравнения определяют отношение между отклонением совета, напряжением и силой совета:

$\begin{array}{l} y_{R} = \frac{l^{2} (4 F_{R} l + 6 d w e_{31} v)}{12 E I} = \frac{l^{2} (4 F_{R} l + 6 d w e_{31} v)}{E w d^{3}} = F_{R} \frac{4 l^{3}}{E w d^{3}} + v \frac{6 e_{31} l^{2}}{E d^{2}} \\ y_{f r e e} = \frac{6 l^{2} d w e_{31} v_{r a t e d}}{12 E I} = \frac{6 e_{31} l^{2} v_{r a t e d}}{E d^{2}} \\ F_{b l o c k} = - \frac{3 d w e_{31} v_{r a t e d}}{2 l} \end{array}$

Блок вычисляет емкость, принимая нулевую приложенную силу:

$C_{p i e z o} = ε \frac{l w}{d} + e_{31}^{2} \frac{l d^{2} w^{2}}{E I} = ε \frac{l w}{d} + e_{31}^{2} \frac{12 l w}{E d} = (ε + 12 \frac{e_{31}^{2}}{E}) \frac{l w}{d} .$

Наконец, это уравнение показывает отношение между плотностью и массой:

$m = ρ l w d .$

Как только вы определили все отношения между основными и параметрами таблицы данных, можно вычислить фундаментальные параметры с помощью этих уравнений:

$\begin{array}{l} e_{31} = - \frac{2 l F_{b l o c k}}{3 d w v_{r a t e d}} \\ E = - \frac{4 F_{b l o c k} l^{3}}{y_{f r e e} d^{3} w} \\ ε = \frac{d}{l w} (C_{p i e z o} + \frac{4 F_{b l o c k} y_{f r e e}}{v_{r a t e d}^{2}}) \end{array}$

Затем подставьте эти уравнения в конститутивные уравнения:

$\begin{array}{l} \frac{v}{v_{r a t e d}} = \frac{F_{R}}{F_{b l o c k}} + \frac{y_{R}}{y_{f r e e}} \\ q = C_{p i e z o} v + \frac{y_{f r e e}}{v_{r a t e d}} F_{R} \end{array}$

Таблица данных динамики

Можно вычислить первую резонансную частоту безжимного луча равномерного сечения при помощи этого уравнения:

$2 π f_{0} = {1.855}^{2} \sqrt{\frac{E I}{m l^{3}}} .$

Затем блок параметрирует динамику непосредственно путем определения желаемой собственной частоты.

Граничные условия

Балки имеют различные граничные условия на левом и правом концах:

Свободно - и перемещение, и вращение равны любому значению.
Просто поддерживается - перемещение равно 0.
Зажим - и перемещение, и вращение равны 0.

В этой таблице показаны возможные граничные строения для пьезогенерирующей балки.

Configuration	Модель
Без зажима
Поддерживаемые
Зажимно-зажимной

Порты

Сохранение

расширить все

`+` - Положительный терминал
электрический

Электрический порт сопоставлен с положительной клеммой пьезоизгиба.

`-` - Отрицательный терминал
электрический

Электрический порт сопоставлен с отрицательной клеммой пьезоизгиба.

`Ctr` - Поступательный случай
механический

Порт механической передачи, связанная с делом.

`Cro` - Вращательный случай
механический

Механический вращательный порт сопоставлен с корпусом.

`Rtr` - Поступательный ротор
механический

Порт механической передачи, сопоставленный с ротором.

`Rro` - Вращательный ротор
механический

Механический вращательный порт сопоставлен с ротором.

Параметры

расширить все

Размерности

`Number of elements` - Количество элементов
`1` (по умолчанию) | положительное целое число, больше или равное 1

Количество элементов, в которых пьезогенерирующий луч дискретизирован с помощью уравнений конечных элементов Эйлера-Бернулли.

`Total beam length` - Общая длина балки
`3.175E-2` `m` (по умолчанию) | положительная скалярная величина

Общая длина балки.

`Beam width` - Ширина луча
`1.27E-2` `m` (по умолчанию) | положительная скалярная величина

Ширина балки.

`Beam thickness` - Толщина балки
`5.08E-4` `m` (по умолчанию) | положительная скалярная величина

Толщина балки.

Установившееся состояние

`Parameterization` - Установившаяся параметризация
`Specify from a datasheet for clamped-free configuration` (по умолчанию) | `Specify from material properties`

Параметризация параметров устойчивого состояния из таблицы данных или из свойств материала.

`Capacitance` - Пьезогенерирующая емкость
`15` `nF` (по умолчанию) | положительная скалярная величина

Емкость пьезогенератора.

Зависимости

Чтобы включить этот параметр, установите Parameterization равным Specify from a datasheet for clamped-free configuration.

`Rated drive voltage, Vrated` - Номинальное напряжение привода
`180` `V` (по умолчанию) | положительная скалярная величина

Номинальное напряжение привода.

Зависимости

Чтобы включить этот параметр, установите Parameterization равным Specify from a datasheet for clamped-free configuration.

`Free deflection at Vrated` - Свободное отклонение при Vrated
`+0.233` `mm` (по умолчанию) | ненулевым значением

Отклонение совета, когда никакая сила не приложена. Знак этого параметра должен отличаться от знака параметра Blocking force at Vrated.

Зависимости

Чтобы включить этот параметр, установите Parameterization равным Specify from a datasheet for clamped-free configuration.

`Blocking force at Vrated` - Блокирующая сила при Vrated
`-0.414` `N` (по умолчанию) | скаляром

Сила, которая обнуляет отклонение совета. Знак этого параметра должен отличаться от знака параметра Free deflection at Vrated.

Зависимости

Чтобы включить этот параметр, установите Parameterization равным Specify from a datasheet for clamped-free configuration.

`Young modulus, E` - Молодой модуль
`1.36628e11` `N/m^2` (по умолчанию) | положительная скалярная величина

Молодой модуль, или модуль упругости в напряжении.

Зависимости

Чтобы включить этот параметр, установите Parameterization равным Specify from material properties.

`Piezoelectric stress coefficient, e31` - Пьезоэлектрический коэффициент напряжения
`7.5459` `C/m^2` (по умолчанию) | ненулевым скаляром

(3,1) пьезоэлектрический коэффициент связи напряжение-заряд.

Зависимости

Чтобы включить этот параметр, установите Parameterization равным Specify from material properties.

`Dielectric constant` - Диэлектрическая константа
`1.38965e-08` `F/m` (по умолчанию) | положительная скалярная величина

Диэлектрическая проницаемость, которая представляет относительную диэлектрическую проницаемость материала. Этот параметр должен быть больше, чем вакуумная диэлектрическая проницаемость.

Зависимости

Чтобы включить этот параметр, установите Parameterization равным Specify from material properties.

Динамика

`Inertial effects` - Опция моделирования инерционных эффектов
`On` (по умолчанию) | `Off`

Моделировать ли инерционные эффекты.

`Parameterization` - Параметризация инерции
`Specify from a datasheet for clamped-free configuration` (по умолчанию) | `Specify from material properties`

Параметризация параметров инерции из таблицы данных или из свойств материала.

Зависимости

Чтобы включить этот параметр, установите Inertial effects равным On.

`Beam mass` - Масса балки
`1.6` `g` (по умолчанию) | положительная скалярная величина

Масса балки.

Зависимости

Чтобы включить этот параметр, установите Inertial effects равным On и Parameterization к Specify from material properties.

`First natural frequency` - Первая естественная частота
`391` `Hz` (по умолчанию) | положительная скалярная величина

Первая естественная частота.

Зависимости

Чтобы включить этот параметр, установите Inertial effects равным On и Parameterization к Specify from a datasheet for clamped-free configuration.

`Rayleigh damping constant proportional to stiffness` - постоянная демпфирования Релея, пропорциональная жесткости
`1e-5` `s` (по умолчанию) | неотрицательной скаляром

Коэффициент демпфирования, пропорциональный жесткости, для демпфирования Релея.

`Rayleigh damping constant proportional to mass` - постоянная демпфирования Релея, пропорциональная массе
`0` `1/s` (по умолчанию) | неотрицательной скаляром

Коэффициент демпфирования, пропорциональный массе, для демпфирования Релея.

Зависимости

Чтобы включить этот параметр, установите Inertial effects равным On.

Примеры моделей

Пьезо Бендер Энергетический Комбайн

Моделируйте устройство, которое собирает энергию от вибрирующего объекта с помощью пьезообменника. Устройство использует эту энергию для зарядки аккумулятора и питания нагрузки.

Ссылки

[1] Tadmor, E. B., and G. Kosa. «Электромеханическая коррекция связи для пьезоэлектрических слоистых пучков». Журнал микроэлектромеханических систем, том 12, № 6, декабрь 2003, стр. 899-906. DOI.org (Crossref), doi:10.1109/JMEMS.2003.820286.

[2] Benjeddou A, Trindade MA, Ohayon R. «Единая модель конечного элемента луча для механизмов продления и сдвига пьезоэлектрических приводов». Журнал интеллектуальных материальных систем и структур. 1997;8(12):1012-1025. doi:10.1177/1045389X9700801202

[3] Гэвин, Анри П. «Beam Element Stiﬀness Matrices». 421L CEE. Матричный структурный анализ. Университет Дьюка, 2014.

Документация

Piezo Bender

Описание

Уравнения

Формулировка конечного элемента

Параметризация таблицы данных

Граничные условия

Порты

Сохранение

+ - Положительный терминал электрический

- - Отрицательный терминал электрический

Ctr - Поступательный случай механический

Cro - Вращательный случай механический

Rtr - Поступательный ротор механический

Rro - Вращательный ротор механический

Параметры

Размерности

Number of elements - Количество элементов 1 (по умолчанию) | положительное целое число, больше или равное 1

Total beam length - Общая длина балки 3.175E-2 m (по умолчанию) | положительная скалярная величина

Beam width - Ширина луча 1.27E-2 m (по умолчанию) | положительная скалярная величина

Beam thickness - Толщина балки 5.08E-4 m (по умолчанию) | положительная скалярная величина

Установившееся состояние

Parameterization - Установившаяся параметризация Specify from a datasheet for clamped-free configuration (по умолчанию) | Specify from material properties

Capacitance - Пьезогенерирующая емкость 15 nF (по умолчанию) | положительная скалярная величина

Зависимости

Rated drive voltage, Vrated - Номинальное напряжение привода 180 V (по умолчанию) | положительная скалярная величина

Зависимости

Free deflection at Vrated - Свободное отклонение при Vrated +0.233 mm (по умолчанию) | ненулевым значением

Зависимости

Blocking force at Vrated - Блокирующая сила при Vrated -0.414 N (по умолчанию) | скаляром

Зависимости

Young modulus, E - Молодой модуль 1.36628e11 N/m^2 (по умолчанию) | положительная скалярная величина

Зависимости

Piezoelectric stress coefficient, e31 - Пьезоэлектрический коэффициент напряжения 7.5459 C/m^2 (по умолчанию) | ненулевым скаляром

Зависимости

Dielectric constant - Диэлектрическая константа 1.38965e-08 F/m (по умолчанию) | положительная скалярная величина

Зависимости

Динамика

Inertial effects - Опция моделирования инерционных эффектов On (по умолчанию) | Off

Parameterization - Параметризация инерции Specify from a datasheet for clamped-free configuration (по умолчанию) | Specify from material properties

Зависимости

Beam mass - Масса балки 1.6 g (по умолчанию) | положительная скалярная величина

Зависимости

First natural frequency - Первая естественная частота 391 Hz (по умолчанию) | положительная скалярная величина

Зависимости

Rayleigh damping constant proportional to stiffness - постоянная демпфирования Релея, пропорциональная жесткости 1e-5 s (по умолчанию) | неотрицательной скаляром

Rayleigh damping constant proportional to mass - постоянная демпфирования Релея, пропорциональная массе 0 1/s (по умолчанию) | неотрицательной скаляром

Зависимости

Примеры моделей

Пьезо Бендер Энергетический Комбайн

Ссылки

Расширенные возможности

Генерация кода C/C + + Сгенерируйте код C и C++ с помощью Coder™ Simulink ®

См. также

Simscape Electrical документация

Поддержка

`+` - Положительный терминал
электрический

`-` - Отрицательный терминал
электрический

`Ctr` - Поступательный случай
механический

`Cro` - Вращательный случай
механический

`Rtr` - Поступательный ротор
механический

`Rro` - Вращательный ротор
механический

`Number of elements` - Количество элементов
`1` (по умолчанию) | положительное целое число, больше или равное 1

`Total beam length` - Общая длина балки
`3.175E-2` `m` (по умолчанию) | положительная скалярная величина

`Beam width` - Ширина луча
`1.27E-2` `m` (по умолчанию) | положительная скалярная величина

`Beam thickness` - Толщина балки
`5.08E-4` `m` (по умолчанию) | положительная скалярная величина

`Parameterization` - Установившаяся параметризация
`Specify from a datasheet for clamped-free configuration` (по умолчанию) | `Specify from material properties`

`Capacitance` - Пьезогенерирующая емкость
`15` `nF` (по умолчанию) | положительная скалярная величина

`Rated drive voltage, Vrated` - Номинальное напряжение привода
`180` `V` (по умолчанию) | положительная скалярная величина

`Free deflection at Vrated` - Свободное отклонение при Vrated
`+0.233` `mm` (по умолчанию) | ненулевым значением

`Blocking force at Vrated` - Блокирующая сила при Vrated
`-0.414` `N` (по умолчанию) | скаляром

`Young modulus, E` - Молодой модуль
`1.36628e11` `N/m^2` (по умолчанию) | положительная скалярная величина

`Piezoelectric stress coefficient, e31` - Пьезоэлектрический коэффициент напряжения
`7.5459` `C/m^2` (по умолчанию) | ненулевым скаляром

`Dielectric constant` - Диэлектрическая константа
`1.38965e-08` `F/m` (по умолчанию) | положительная скалярная величина

`Inertial effects` - Опция моделирования инерционных эффектов
`On` (по умолчанию) | `Off`

`Parameterization` - Параметризация инерции
`Specify from a datasheet for clamped-free configuration` (по умолчанию) | `Specify from material properties`

`Beam mass` - Масса балки
`1.6` `g` (по умолчанию) | положительная скалярная величина

`First natural frequency` - Первая естественная частота
`391` `Hz` (по умолчанию) | положительная скалярная величина

`Rayleigh damping constant proportional to stiffness` - постоянная демпфирования Релея, пропорциональная жесткости
`1e-5` `s` (по умолчанию) | неотрицательной скаляром

`Rayleigh damping constant proportional to mass` - постоянная демпфирования Релея, пропорциональная массе
`0` `1/s` (по умолчанию) | неотрицательной скаляром

Генерация кода C/C + +
Сгенерируйте код C и C++ с помощью Coder™ Simulink ®