widebandTwoRayChannel

Широкополосный двухлучевой канал распространения

Описание

The widebandTwoRayChannel моделирует широкополосный двухлучевой канал распространения. Двухлучевой канал распространения является самым простым типом многолучевого канала. Можно использовать двухлучевой канал, чтобы симулировать распространение сигналов в однородной, изотропной среде с одной отражающим контуром. Этот тип среды имеет два пути распространения: путь распространения линии визирования (прямого) от одной точки к другой и путь луча, отраженный от контура.

Вы можете использовать эту object™ System для приложений радиолокации и мобильной связи малой дальности, где сигналы распространяются по прямым путям, а Земля принята плоской. Можно также использовать этот объект для гидроакустических и микрофонных приложений. Для акустических приложений можно выбрать неполяризованные поля и настроить скорость распространения так, чтобы она была скоростью звука в воздухе или воде. Можно использовать widebandTwoRayChannel для моделирования распространения из нескольких точек одновременно.

Несмотря на то, что системный объект работает для всех частот, модели ослабления для атмосферных газов и дождя действительны только для электромагнитных сигналов в частотной области значений 1-1000 ГГц. Модель ослабления для тумана и облака действительна для 10-1000 ГГц. Вне этих областей значений частот системный объект использует самое близкое допустимое значение.

The widebandTwoRayChannel Системный объект применяет зависящие от области значений задержки времени к сигналам, а также усиления или потери, сдвиги фазы и краевые потери отражения. Когда источник или пункт назначения перемещается, системный объект применяет доплеровские сдвиги к сигналам.

Сигналы на выходе канала могут храниться отдельно или быть объединены. Если вы сохраняете сигналы раздельными, оба сигнала поступают в пункт назначения отдельно и не объединяются. Если вы принимаете решение объединить сигналы, два сигнала от источника распространяются отдельно, но когерентно суммируются в пункте назначения в одну величину. Выберите эту опцию, когда различие между усилениями датчика или массива в направлениях двух путей незначительна.

В отличие от phased.WidebandFreeSpace и phased.WidebandLOSChannel Системные объекты, этот Системный объект не поддерживает двухстороннее распространение.

Чтобы вычислить задержку распространения для заданных точек источника и приемника:

Определите и настройте свой двухлучевой канал. См. «Конструкция».
Вызовите step метод вычисления распространенного сигнала с использованием свойств widebandTwoRayChannel Системный объект.

Примечание

Кроме того, вместо использования step метод для выполнения операции, заданной системным объектом, можно вызвать объект с аргументами, как если бы это была функция. Для примера, y = step(obj,x) и y = obj(x) выполнять эквивалентные операции.

Конструкция

channel = widebandTwoRayChannel создает двухлучевой канал распространения Системного объекта, channel.

channel = widebandTwoRayChannel(Name,Value) создает Системный объект, channel, с каждым заданным свойством Name установить на заданную Value. Можно задать дополнительные аргументы в виде пар имен и значений в любом порядке как (Name1,Value1..., NameN,ValueN).

Свойства

расширить все

`PropagationSpeed` - Скорость распространения сигнала
`physconst('LightSpeed')` (по умолчанию) | положительная скалярная величина

Скорость распространения сигнала, заданная как положительная скалярная величина. Модули указаны в метрах в секунду. Скорость распространения по умолчанию является значением, возвращаемым physconst('LightSpeed'). Посмотрите physconst для получения дополнительной информации.

Пример: 3e8

Типы данных: double

`OperatingFrequency` - Рабочая частота
`300e6` (по умолчанию) | положительная скалярная величина

Рабочая частота, заданная как положительная скалярная величина. Модули указаны в Гц.

Пример: 1e9

Типы данных: double

`SpecifyAtmosphere` - Включите модель атмосферного ослабления
`false` (по умолчанию) | `true`

Опция для включения атмосферной модели ослабления, заданная как false или true. Установите это свойство на true добавить ослабление сигнала, вызванное атмосферными газами, дождем, туманом или облаками. Установите это свойство на false игнорировать атмосферные эффекты при распространении.

`NumSubbands` - Количество обрабатывающих поддиапазонов
`64` (по умолчанию) | положительное целое число

Количество обрабатывающих поддиапазонов, заданное как положительное целое число.

Пример: 128

Типы данных: double

`EnablePolarization` - Включите поляризованные поля
`false` (по умолчанию) | `true`

Опция включения поляризованных полей, заданная как false или true. Установите это свойство на true для обеспечения поляризации. Установите это свойство на false чтобы игнорировать поляризацию.

Типы данных: logical

`GroundReflectionCoefficient` - Коэффициент отражения земли
`-1` (по умолчанию) | скалярный скаляр | комплексным вектором 1-байт- N строки

Коэффициент отражения земли для поля в точке отражения, заданный как комплексный скаляр или комплексный вектор-строка 1- N. Каждый коэффициент имеет абсолютное значение, меньше чем или равное единице. Величина N является количеством двухлучевых каналов. Модули безразмерны. Используйте это свойство для модели неполяризованных сигналов. Чтобы смоделировать поляризованные сигналы, используйте GroundRelativePermittivity свойство.

Пример: -0.5

Зависимости

Чтобы включить это свойство, задайте EnablePolarization на false.

Типы данных: double
Поддержка комплексного числа: Да

`GroundRelativePermittivity` - Относительная диэлектрическая проницаемость грунта
`15` (по умолчанию) | положительный скаляр с реальным значением | вектор положительных значений 1- N строки с реальным значением

Относительная диэлектрическая проницаемость земли в точке отражения, заданная как положительный действительный скаляр или 1-байтовый N действительный вектор-строка положительных значений. Размерная N является количеством двухлучевых каналов. Модули диэлектрической проницаемости безразмерны. Относительная диэлектрическая проницаемость определяется как отношение фактической диэлектрической проницаемости грунта к диэлектрической проницаемости свободного пространства. Это свойство применяется, когда вы устанавливаете EnablePolarization свойство к true. Используйте это свойство для модели поляризованных сигналов. Чтобы смоделировать неполяризованные сигналы, используйте GroundReflectionCoefficient свойство.

Пример: 5

Зависимости

Чтобы включить это свойство, задайте EnablePolarization на true.

Типы данных: double

`CombinedRaysOutput` - Опция объединения двух лучей на выходе
`true` (по умолчанию) | `false`

Опция для объединения двух лучей на выходе канала, заданная как true или false. Когда это свойство trueобъект когерентно складывает сигнал распространения линии визирования и отраженный сигнал пути при формировании сигнала выхода. Используйте этот режим, когда вам не нужно включать в симуляцию направленный коэффициент усиления антенны или массива.

Типы данных: logical

`MaximumDistanceSource` - Источник максимального одностороннего расстояния распространения
`'Auto'` (по умолчанию) | `'Property'`

Источник максимального одностороннего расстояния распространения, заданный как 'Auto' или 'Property'. Максимальное одностороннее расстояние распространения используется, чтобы выделить достаточное количество памяти для расчета задержки сигнала. Когда вы устанавливаете это свойство на 'Auto'Системный объект автоматически выделяет память. Когда вы устанавливаете это свойство на 'Property', вы задаете максимальное одностороннее расстояние распространения, используя значение MaximumDistance свойство.

Типы данных: char

`MaximumDistance` - Максимальное одностороннее расстояние распространения
`10000` (по умолчанию) | положительный скаляр с реальным значением

Максимальное одностороннее расстояние распространения, заданное как положительный действительный скаляр. Модули измерения указаны в метрах. Любой сигнал, который распространяется больше, чем максимальное одностороннее расстояние, игнорируется. Максимальное расстояние должно быть больше или равно наибольшему расстоянию между положениями.

Пример: 5000

Зависимости

Чтобы включить это свойство, установите MaximumDistanceSource свойство к 'Property'.

Типы данных: double

`MaximumNumInputSamplesSource` - Источник максимального количества выборок
`'Auto'` (по умолчанию) | `'Property'`

Источник максимального количества выборок входного сигнала, заданный как 'Auto' или 'Property'. Когда вы устанавливаете это свойство на 'Auto'модель распространения автоматически выделяет достаточно памяти, чтобы буферизировать входной сигнал. Когда вы устанавливаете это свойство на 'Property', вы задаете максимальное количество выборок во входном сигнале используя MaximumNumInputSamples свойство. Любой входной сигнал, длиннее этого значения, усечен.

Чтобы использовать этот объект с сигналами переменного размера в MATLAB^® Функциональный блок в Simulink^®, установите MaximumNumInputSamplesSource свойство к 'Property' и установите значение для MaximumNumInputSamples свойство.

Пример: 'Property'

Зависимости

Чтобы включить это свойство, задайте MaximumDistanceSource на 'Property'.

Типы данных: char

`MaximumNumInputSamples` - Максимальное количество выборок входного сигнала
`100` (по умолчанию) | положительное целое число

Максимальное количество выборок входного сигнала, заданное как положительное целое число. Входной сигнал является первым аргументом step метод, после самого системного объекта. Размер входного сигнала является количеством строк в вход матрице. Любой входной сигнал, длиннее этого числа, усечен. Чтобы полностью обработать сигналы, убедитесь, что это значение свойства больше, чем любая максимальная длина входного сигнала.

Системные объекты, генерирующие форму волны, определяют максимальный размер сигнала:

Для любой формы волны, если форма волны OutputFormat для свойства задано значение 'Samples', максимальная длина сигнала является значением, заданным в NumSamples свойство.
Для импульсных сигналов, если OutputFormat установлено в 'Pulses', длина сигнала является продуктом наименьшей частоты повторения импульса, количества импульсов и частоты дискретизации.
Для непрерывных форм волны, если OutputFormat установлено в 'Sweeps', длина сигнала является продуктом времени свипа, количества свипов и частоты дискретизации.

Пример: 2048

Зависимости

Чтобы включить это свойство, задайте MaximumNumInputSamplesSource на 'Property'.

Типы данных: double

Методы

сброс	Сброс состояний системного объекта
шаг	Распространите широкополосный сигнал от точки к точке с помощью модели двухлучевого канала

Общий для всех системных объектов
`release`	Разрешить изменение значения свойства системного объекта

Примеры

свернуть все

Скалярный широкополосный сигнал, распространяющийся в двухлучевом канале

Открыть Live Script

Этот пример иллюстрирует двухлучевое распространение широкополосного сигнала, показывая, как сигналы из линии видимости и отраженного пути поступают в приемник в разное время.

Примечание: Можно заменить каждый вызов функции эквивалентным step синтаксис. Для примера замените myObject(x) с step(myObject,x).

Создайте и постройте график переданной формы волны

Создайте неполяризованное электромагнитное поле, состоящее из двух линейных FM импульсов формы волны на несущей частоте 100 МГц. Предположим, что ширина импульса составляет 20 мкс, а частота дискретизации - 10 МГц. Шумовая полоса импульса составляет 1 МГц. Примите коэффициент заполнения 50%, так что ширина импульса составляет половину интервала повторения импульса. Создайте train с двумя импульсными волнами. Установите GroundReflectionCoefficient до -0,9 для моделирования сильной отражательной способности грунта. Передайте поле от стационарного источника к стационарному приемнику. Вертикальное разделение источника и приемника составляет приблизительно 10 км.

c = physconst('LightSpeed');
fs = 10e6;
pw = 20e-6;
pri = 2*pw;
PRF = 1/pri;
fc = 100e6;
lambda = c/fc;
bw = 1e6;
waveform = phased.LinearFMWaveform('SampleRate',fs,'PulseWidth',pw,...
    'PRF',PRF,'OutputFormat','Pulses','NumPulses',2,'SweepBandwidth',bw,...
    'SweepDirection','Down','Envelope','Rectangular','SweepInterval',...
    'Positive');
wav = waveform();
n = size(wav,1);
plot([0:(n-1)]/fs*1e6,real(wav),'b')
xlabel('Time (\mu s)')
ylabel('Waveform Magnitude')

Figure contains an axes. The axes contains an object of type line.

Укажите местоположение источника и приемника

Разместите источник и приемник на расстоянии около 1 км друг от друга по горизонтали и приблизительно 5 км по вертикали.

pos1 = [0;0;100];
pos2 = [1e3;0;5.0e3];
vel1 = [0;0;0];
vel2 = [0;0;0];

Создайте широкополосный двухлучевой канал Системного объекта

Создайте двухлучевой канал распространения System object™ и распространите сигнал как вдоль линии видимости, так и вдоль отраженных лучевых путей. Один и тот же сигнал распространяется по обоим путям.

channel = widebandTwoRayChannel('SampleRate',fs,...
    'GroundReflectionCoefficient',-0.9,'OperatingFrequency',fc,...
    'CombinedRaysOutput',false);
prop_signal = channel([wav,wav],pos1,pos2,vel1,vel2);

[rng2,angs] = rangeangle(pos2,pos1,'two-ray');

Вычислите задержки в мкс.

tm = rng2/c*1e6;
disp(tm)

   16.6815   17.3357

Отобразите вычисленные пути распространения азимута и углов возвышения в степени.

disp(angs)

         0         0
   78.4654  -78.9063

Постройте график распространенных сигналов

Постройте график действительной части сигнала, распространяемой вдоль пути видимости.
Постройте график действительной части сигнала, распространенной вдоль отраженного пути.
Постройте график действительной части когерентной суммы двух сигналов.

n = size(prop_signal,1);
delay = [0:(n-1)]/fs*1e6;
subplot(3,1,1)
plot(delay,real([prop_signal(:,1)]),'b')
grid
xlabel('Time (\mu sec)')
ylabel('Real Part')
title('Direct Path')

subplot(3,1,2)
plot(delay,real([prop_signal(:,2)]),'b')
grid
xlabel('Time (\mu sec)')
ylabel('Real Part')
title('Reflected Path')

subplot(3,1,3)
plot(delay,real([prop_signal(:,1) + prop_signal(:,2)]),'b')
grid
xlabel('Time (\mu sec)')
ylabel('Real Part')
title('Combined Paths')

Figure contains 3 axes. Axes 1 with title Direct Path contains an object of type line. Axes 2 with title Reflected Path contains an object of type line. Axes 3 with title Combined Paths contains an object of type line.

Задержка отраженного сигнала пути согласуется с предсказанной задержкой. Величина когерентно объединенного сигнала меньше, чем любой из распространенных сигналов. Этот результат указывает, что эти два сигнала содержат некоторую интерференцию.

Сравнение широкополосного двухлучевого распространения канала к свободному пространству

Открыть Live Script

Вычислите результат распространения широкополосного сигнала LFM в двухлучевом окружении от радара на 10 метра высокого источника (0,0,10) до цели на (3000,2000,2000) метрах. Предположим, что радар и цель являются стационарными и что передающая антенна изотропна. Объедините сигнал от двух путей и сравните сигнал с сигналом, распространяющимся в свободном пространстве. Система работает на частоте 300 МГц. Установите CombinedRaysOutput свойство к true для объединения сигналов прямого пути и отраженного пути при формировании сигнала выхода.

Примечание.Этот пример выполняется только в R2016b или более поздней версии. Если вы используете более ранний релиз, замените каждый вызов функции на эквивалентный step синтаксис. Для примера замените myObject(x) с step(myObject,x).

Создайте линейную FM-форму волны.

fop = 300.0e6;
fs = 1.0e6;
waveform = phased.LinearFMWaveform();
x = waveform();

Задайте целевое положение и скорость.

posTx = [0; 0; 10];
posTgt = [3000; 2000; 2000];
velTx = [0;0;0];
velTgt = [0;0;0];

Моделируйте распространение свободного пространства.

fschannel = phased.WidebandFreeSpace('SampleRate',waveform.SampleRate);
y_fs = fschannel(x,posTx,posTgt,velTx,velTgt);

Моделируйте распространение двух лучей от положения радара до цели.

tworaychannel = widebandTwoRayChannel('SampleRate',waveform.SampleRate,...
    'CombinedRaysOutput',true);
y_tworay = tworaychannel(x,posTx,posTgt,velTx,velTgt);
plot(abs([y_tworay y_fs]))
legend('Wideband two-ray (Position 1)','Wideband free space (Position 1)',...
    'Location','best')
xlabel('Samples')
ylabel('Signal Magnitude')
hold on

Figure contains an axes. The axes contains 2 objects of type line. These objects represent Wideband two-ray (Position 1), Wideband free space (Position 1).

Переместите радар на 10 метров по горизонтали во второе положение.

posTx = posTx + [10;0;0];
y_fs = fschannel(x,posTx,posTgt,velTx,velTgt);
y_tworay = tworaychannel(x,posTx,posTgt,velTx,velTgt);
plot(abs([y_tworay y_fs]))
legend('Wideband two-ray (Position 1)','Wideband free space (Position 1)',...
    'Wideband two-ray (Position 2)','Wideband free space (Position 2)',...
    'Location','best')
hold off

Figure contains an axes. The axes contains 4 objects of type line. These objects represent Wideband two-ray (Position 1), Wideband free space (Position 1), Wideband two-ray (Position 2), Wideband free space (Position 2).

Потери распространения свободного пространства одинаковы как для первого, так и для второго положения радара. Двухлучевые потери различаются из-за интерференционного эффекта двухлучевых путей.

Широкополосное поляризованное распространение поля в двухлучевом канале

Открыть Live Script

Создайте поляризованное электромагнитное поле, состоящее из линейных FM импульсов формы волны. Распространите поле от стационарного источника с перекрестно-дипольным антенным элементом на стационарный приемник примерно в 10 км. Передающая антенна находится на высоте 100 м над землей. Приемная антенна находится на высоте 150 м над уровнем земли. Приемная антенна также является перекрестным диполем. Постройте график принимаемого сигнала.

Установите параметры формы волны радара

Предположим, что ширина импульса равна $10 μ s$ и частота дискретизации составляет 10 МГц. Шумовая полоса импульса составляет 1 МГц. Примите 50% коэффициент заполнения, в котором ширина импульса составляет половину интервала повторения импульса. Создайте train с двумя импульсными волнами. Предположим, что несущая частота составляет 100 МГц.

c = physconst('LightSpeed');
fs = 20e6;
pw = 10e-6;
pri = 2*pw;
PRF = 1/pri;
fc = 100e6;
bw = 1e6;
lambda = c/fc;

Настройка необходимых системных объектов

Использование GroundRelativePermittivity из 10.

waveform = phased.LinearFMWaveform('SampleRate',fs,'PulseWidth',pw,...
    'PRF',PRF,'OutputFormat','Pulses','NumPulses',2,'SweepBandwidth',bw,...
    'SweepDirection','Down','Envelope','Rectangular','SweepInterval',...
    'Positive');
antenna = phased.CrossedDipoleAntennaElement(...
    'FrequencyRange',[50,200]*1e6);
radiator = phased.Radiator('Sensor',antenna,'OperatingFrequency',fc,...
    'Polarization','Combined');
channel = phased.WidebandTwoRayChannel('SampleRate',fs,...
    'OperatingFrequency',fc,'CombinedRaysOutput',false,...
    'EnablePolarization',true,'GroundRelativePermittivity',10);
collector = phased.Collector('Sensor',antenna,'OperatingFrequency',fc,...
    'Polarization','Combined');

Настройка геометрии сцены

Задайте положения передатчика и приемника, скорости и ориентации. Разместите источник и приемник приблизительно на 1000 м друг от друга в горизонтальном направлении и приблизительно на 50 м в вертикальном направлении.

posTx = [0;100;100];
posRx = [1000;0;150];
velTx = [0;0;0];
velRx = [0;0;0];
laxRx = rotz(180);
laxTx = rotx(1)*eye(3);

Создавайте и излучайте сигналы от передатчика

Вычислите углы передачи для двух лучей, движущихся к приемнику. Эти углы заданы относительно локальной системы координат передатчика. The phased.Radiator System object(TM) использует эти углы, чтобы применить отдельные усиления антенны к этим двум сигналам.

[rng,angsTx] = rangeangle(posRx,posTx,laxTx,'two-ray');
wav = waveform();

Постройте график переданной формы волны.

n = size(wav,1);
plot([0:(n-1)]/fs*1000000,real(wav))
xlabel('Time ({\mu}sec)')
ylabel('Waveform')

Figure contains an axes. The axes contains an object of type line.

sig = radiator(wav,angsTx,laxTx);

Передайте сигналы в приемник через двухлучевой канал.

prop_sig = channel(sig,posTx,posRx,velTx,velRx);

Прием распространенного сигнала

Вычислите углы приема для двух лучей, поступающих в приемник. Эти углы заданы относительно локальной системы координат приемника. The phased.Collector System object(TM) использует эти углы, чтобы применить отдельные усиления антенны к этим двум сигналам.

[rng1,angsRx] = rangeangle(posTx,posRx,laxRx,'two-ray');
delays = rng1/c*1e6

delays = 1×2

    3.3564    3.4544

Собирайте и комбинируйте полученные лучи.

y = collector(prop_sig,angsRx,laxRx);

Постройте график полученной формы волны.

plot([0:(n-1)]/fs*1000000,real(y))
xlabel('Time ({\mu}sec)')
ylabel('Received Waveform')

Figure contains an axes. The axes contains an object of type line.

Двухлучевое распространение широкополосной волны LFM с атмосферными потерями

Открыть Live Script

Распространите широкополосный линейный FM сигнал в двухлучевом канале. Шумовая полоса сигнала составляет 15% от частоты несущей. Предположим, что происходит потеря сигнала, вызванная атмосферными газами и дождем. Сигнал распространяется от передатчика, расположенного в (0,0,0) счетчики в глобальной системе координат в приемник в (10000,200,30) метров. Предположим, что передатчик и приемник являются стационарными и что они оба имеют косинусоидные шаблоны. Постройте график принимаемого сигнала. Установите давление сухого воздуха 102,0 Па и скорость дождя 5 мм/ч.

Установите параметры формы волны радара

c = physconst('LightSpeed');
fs = 40e6;
pw = 10e-6;
pri = 2.5*pw;
PRF = 1/pri;
fc = 100e6;
bw = 15e6;
lambda = c/fc;

Настройка радиолокационного сценария

Создайте необходимые системные объекты.

waveform = phased.LinearFMWaveform('SampleRate',fs,'PulseWidth',pw,...
    'PRF',PRF,'OutputFormat','Pulses','NumPulses',2,'SweepBandwidth',bw,...
    'SweepDirection','Down','Envelope','Rectangular','SweepInterval',...
    'Positive');
antenna = phased.CosineAntennaElement;
radiator = phased.Radiator('Sensor',antenna);
collector = phased.Collector('Sensor',antenna);
channel = widebandTwoRayChannel('SampleRate',waveform.SampleRate,...
    'CombinedRaysOutput',false,'GroundReflectionCoefficient',0.95,...
    'SpecifyAtmosphere',true,'Temperature',20,...
    'DryAirPressure',102.5,'RainRate',5.0);

Настройте геометрию сцены. Задайте положения и скорости передатчика и приемника. Передатчик и приемник являются стационарными.

posTx = [0;0;0];
posRx = [10000;200;30];
velTx = [0;0;0];
velRx = [0;0;0];

Задайте ориентации передающей и приемной радиолокационных антенн относительно глобальных координат. Передающая антенна точек вдоль положительного направления x, а приемной антенны точек близко к отрицательному направлению x.

laxTx = eye(3);
laxRx = rotx(5)*rotz(170);

Вычислите углы передачи, которые являются углами, под которыми два луча, движущиеся к приемнику, покидают передатчик. The phased.Radiator Система object™ использует эти углы, чтобы применить отдельные усиления антенны к двум сигналам. Поскольку усиления антенны зависят от направления пути, вы должны передавать и принимать два луча отдельно.

[~,angTx] = rangeangle(posRx,posTx,laxTx,'two-ray');

Создавайте и излучайте сигналы от передатчика

Излучайте сигналы по направлениям передачи.

wavfrm = waveform();
wavtrans = radiator(wavfrm,angTx);

Передайте сигналы в приемник через двухлучевой канал.

wavrcv = channel(wavtrans,posTx,posRx,velTx,velRx);

Сбор сигнала в приемнике

Вычислите угол, при котором два луча, перемещающиеся от передатчика, поступают в приемник. The phased.Collector Система object™ использует эти углы, чтобы применить отдельные усиления антенны к двум сигналам.

[~,angRcv] = rangeangle(posTx,posRx,laxRx,'two-ray');

Соберите и объедините два полученных луча.

yR = collector(wavrcv,angRcv);

Постройте график принимаемого сигнала

dt = 1/waveform.SampleRate;
n = size(yR,1);
plot([0:(n-1)]*dt*1e6,real(yR))
xlabel('Time ({\mu}sec)')
ylabel('Signal Magnitude')

Figure contains an axes. The axes contains an object of type line.

Подробнее о

расширить все

Двухлучевые пути распространения

Двухлучевой канал распространения является следующим шагом вверх по сложности от канала свободного пространства и является простейшим случаем многолучевого окружения распространения. Канал свободного пространства моделирует прямолинейный путь наблюдения от точки 1 до точки 2. В двухлучевом канале среда задается как однородная, изотропная среда с отражающим планарным контуром. Значение контура всегда устанавливается на z = 0. Существует не более двух лучей, распространяющихся от точки 1 до точки 2. Первый путь луча распространяется вдоль того же пути видимости, что и в канале свободного пространства. Линейный путь часто называют прямой путь. Второй луч отражается вне контура перед распространением в точку 2. Согласно Закону Отражения, угол отражения равен углу падения. В ближних симуляциях, таких как сотовые коммуникационные системы и автомобильные радары, можно предположить, что отражающая поверхность, земля или поверхность океана, плоская.

The twoRayChannel и widebandTwoRayChannel Системные объекты модели задержку распространения, сдвиг фазы, доплеровский сдвиг и эффекты потерь для обоих путей. Для отраженного пути эффекты потерь включают потери отражения на контуре.

Рисунок иллюстрирует два пути распространения. Из исходной позиции, _ss и позиции приемника, _sr, можно вычислить углы прихода обоих путей, _θ′los и _θ′rp. Углы прихода являются углами повышения и азимута поступающего излучения относительно локальной системы координат. В этом случае локальная система координат совпадает с глобальной системой координат. Можно также вычислить углы передачи, _θlos и _θrp. В глобальных координатах угол отражения на контуре совпадает с углами _θrp и _θ′rp. Угол отражения важно знать, когда вы используете зависящие от угла данные отражений и потерь. Можно определить угол отражения при помощи rangeangle функция и установка ссылочных осей в глобальную систему координат. Общая длина пути для линии визирования показана на рисунке по _Rlos, которая равна геометрическому расстоянию между источником и приемником. Общая длина пути для отраженного пути _{Rrp= R1 + R2}. Количественный L является наземной областью значений между источником и приемником.

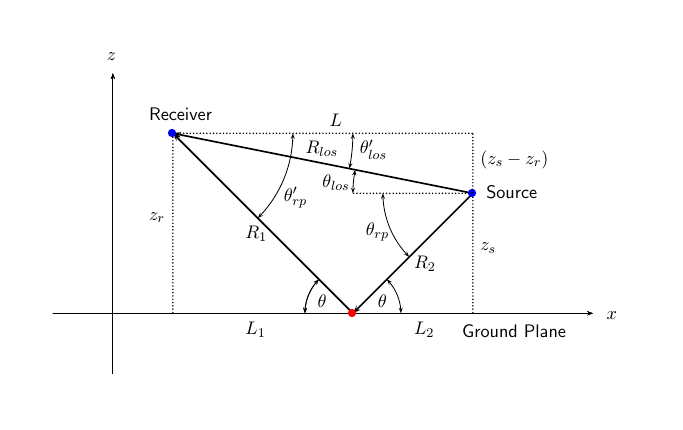
Можно легко вывести точные формулы для длин и углов пути с точки зрения области значений земли и высот объектов в глобальной системе координат.

$\begin{array}{l} \vec{R} = {\vec{x}}_{s} - {\vec{x}}_{r} \\ R_{l o s} = | \vec{R} | = \sqrt{{(z_{r} - z_{s})}^{2} + L^{2}} \\ R_{1} = \frac{z_{r}}{z_{r} + z_{z}} \sqrt{{(z_{r} + z_{s})}^{2} + L^{2}} \\ R_{2} = \frac{z_{s}}{z_{s} + z_{r}} \sqrt{{(z_{r} + z_{s})}^{2} + L^{2}} \\ R_{r p} = R_{1} + R_{2} = \sqrt{{(z_{r} + z_{s})}^{2} + L^{2}} \\ \tan θ_{l o s} = \frac{(z_{s} - z_{r})}{L} \\ \tan θ_{r p} = - \frac{(z_{s} + z_{r})}{L} \\ {θ^{'}}_{l o s} = - θ_{l o s} \\ {θ^{'}}_{r p} = θ_{r p} \end{array}$

Двухлучевое ослабление

Ослабление или потери пути в двухлучевом канале являются продуктом пяти компонентов, _{L = Ltworay LG Lg Lc Lr}, где

_Ltworay - двухлучевое геометрическое ослабление пути
_LG - затухание отражения земли
_Lg - ослабление атмосферного пути
_Lc - ослабление тумана и пути облака
_Lr - ослабление дождевого пути

Каждый компонент находится в модулях величины, а не в дБ.

Отражение земли и потери распространения

Потери происходят, когда сигнал отражается от контура. Можно получить простую модель потерь отражения земли путем представления электромагнитного поля как скалярного поля. Этот подход также работает для акустических и гидроакустических систем. Позвольте E быть скалярным электромагнитным полем свободного пространства, имеющим амплитуду, _E0 на исходном расстоянии, _R0 от передатчика (например, один метр). Распространяющееся поле свободного пространства на расстоянии _Rlos от передатчика,

$E_{l o s} = E_{0} (\frac{R_{0}}{R_{l o s}}) e^{i ω (t - R_{l o s} / c)}$

для пути видимости. Можно выразить отраженное землей E -поле как

$E_{r p} = L_{G} E_{0} (\frac{R_{0}}{R_{r p}}) e^{i ω (t - R_{r p} / c)}$

где _Rrp - расстояние отраженного пути. Количество, _LG представляет потерю из-за отражения в плоскости земли. Чтобы задать _LG, используйте GroundReflectionCoefficient свойство. В целом _LG зависит от угла падения поля. Если у вас есть эмпирическая информация об угловой зависимости _LG, можно использовать rangeangle вычислить угол падения отраженного пути. Общее поле в пункте назначения является суммой полей видимости и отраженного пути.

Для электромагнитных волн более сложная, но более реалистичная модель использует вектор представление поляризованного поля. Можно разложить падающее электрическое поле на два компонента. Один компонент, _Ep, параллелен плоскости падения. Другой компонент, _Es, перпендикулярен плоскости падения. Коэффициенты отражения земли для этих компонентов различаются и могут быть записаны с точки зрения проницаемости земли и угла падения.

$\begin{array}{l} G_{p} = \frac{Z_{1} \cos θ_{1} - Z_{2} \cos θ_{2}}{Z_{1} \cos θ_{1} + Z_{2} \cos θ_{2}} = \frac{\cos θ_{1} - \frac{Z_{2}}{Z_{1}} \cos θ_{2}}{\cos θ_{1} + \frac{Z_{2}}{Z_{1}} \cos θ_{2}} \\ G_{s} = \frac{Z_{2} \cos θ_{1} - Z_{1} \cos θ_{2}}{Z_{2} \cos θ_{1} + Z_{1} \cos θ_{2}} = \frac{\cos θ_{2} - \frac{Z_{2}}{Z_{1}} \cos θ_{1}}{\cos θ_{2} + \frac{Z_{2}}{Z_{1}} \cos θ_{1}} \\ Z_{1} = \sqrt{\frac{μ_{1}}{ε_{1}}} \\ Z_{2} = \sqrt{\frac{μ_{2}}{ε_{2}}} \end{array}$

где Z - импеданс среды. Поскольку магнитная проницаемость Земли почти идентична магнитной проницаемости воздуха или свободного пространства, отношение импедансов зависит, в основном, от отношения электрических проницаемостей

$\begin{array}{l} G_{p} = \frac{\sqrt{ρ} \cos θ_{1} - \cos θ_{2}}{\sqrt{ρ} \cos θ_{1} + \cos θ_{2}} \\ G_{s} = \frac{\sqrt{ρ} \cos θ_{2} - \cos θ_{1}}{\sqrt{ρ} \cos θ_{2} + \cos θ_{1}} \end{array}$

где _{ρ = ε2/ε1} величины является заземленной относительной диэлектрической проницаемостью, заданной GroundRelativePermittivity свойство. Угол _θ1 является углом падения, а угол _θ2 является углом преломления на контуре. Можно определить _θ2 с помощью закона преломления Снелла.

После отражения полное поле восстанавливается из параллельных и перпендикулярных компонентов. Полное затухание наземной плоскости, _LG, является комбинацией _Gs и _Gp.

Когда источник и пункт назначения являются стационарными относительно друг друга, можно записать выход Y от step как Y(t) = F(t-τ)/L. Величина τ является задержкой сигнала, и L является потерями при распространении в свободном пространстве. τ задержки задается R/c. R - это или расстояние пути распространения линии визирования, или расстояние отраженного пути, и c является скоростью распространения. Потери пути

$L_{t w o r a y} = \frac{{(4 π R)}^{2}}{λ^{2}},$

где λ - длина волны сигнала.

Модель ослабления атмосферного газа

Эта модель вычисляет ослабление сигналов, которые распространяются через атмосферные газы.

Электромагнитные сигналы ослабевают, когда они распространяются через атмосферу. Этот эффект вызван в основном линиями поглощения резонанса кислорода и водяного пара с меньшими вкладами, поступающими от газообразного азота. Модель также включает непрерывный спектр поглощения ниже 10 ГГц. Используется модель МСЭ Рекомендация ITU-R P.676-10: Ослабление атмосферными газами. Модель вычисляет удельное ослабление (ослабление на километр) как функцию от температуры, давления, плотности водяного пара и частоты сигнала. Модель атмосферного газа действительна для частот от 1 до 1000 ГГц и применяется к поляризованным и неполяризованным полям.

Формула для определенного ослабления на каждой частоте является

$γ = γ_{o} (f) + γ_{w} (f) = 0.1820 f N^{″} (f) .$

Количественная N"() является мнимой частью комплексной атмосферной рефрактивности и состоит из спектральной линии компонента и непрерывного компонента:

$N^{″} (f) = \sum_{i} S_{i} F_{i} + {N^{″}}_{D}^{} (f)$

Спектральный компонент состоит из суммы дискретных членов спектра, состоящих из локализованной функции полосы частот, F(f) i, умноженной на интенсивность спектральной линии, _S i. Для атмосферного кислорода каждая спектральная прочность линии

$S_{i} = a_{1} \times 10^{- 7} {(\frac{300}{T})}^{3} \exp [a_{2} (1 - (\frac{300}{T})] P .$

Для атмосферного водяного пара каждая спектральная прочность линии

$S_{i} = b_{1} \times 10^{- 1} {(\frac{300}{T})}^{3.5} \exp [b_{2} (1 - (\frac{300}{T})] W .$

P - давление сухого воздуха, W - парциальное давление водяного пара, и T - температура окружающей среды. Модули давления находятся в hectoPascals (hPa), а температура в степенях Кельвина. Парциальное давление водяного пара, W, связано с плотностью водяного пара,

$W = \frac{ρ T}{216.7} .$

Общее атмосферное давление составляет P + W.

Для каждой кислородной линии _Si зависит от двух параметров, _a1 и _a2. Точно так же каждая линия водяного пара зависит от двух параметров, _b1 и _b2. Документация ITU, приведенная в конце этого раздела, содержит таблицы этих параметров как функций частоты.

Локализованные функции полосы частот _Fi(f) являются сложными функциями частоты, описанными в ссылках ITU, цитируемых ниже. Функции зависят от эмпирических параметров модели, которые также сведены в таблицу в ссылке.

Чтобы вычислить общее ослабление для узкополосных сигналов вдоль пути, функция умножает конкретное ослабление на длину пути, R. Затем общее ослабление _{Lg= R(γo + γw)}.

Можно применить модель ослабления к широкополосным сигналам. Сначала разделите широкополосный сигнал на частотные поддиапазоны и примените ослабление к каждому поддиапазону. Затем суммируйте все ослабленные поддиапазонные сигналы в полный ослабленный сигнал.

Модель ослабления тумана и облака

Эта модель вычисляет ослабление сигналов, которые распространяются через туман или облака.

Туман и затухание облака - одно и то же атмосферное явление. Используется модель ITU, Рекомендация ITU-R P.840-6: Ослабление из-за облаков и тумана. Модель вычисляет удельное ослабление (ослабление на километр) сигнала как функцию от плотности жидкости, частоты сигнала и температуры. Модель применяется к поляризованным и неполяризованным полям. Формула для определенного ослабления на каждой частоте является

$γ_{c} = K_{l} (f) M,$

где M - плотность жидкой воды в г/м³. Величина _Kl(f) является определенным коэффициентом ослабления и зависит от частоты. Модель ослабления облака и тумана действует для частот 10-1000 ГГц. Модулями для конкретного коэффициента ослабления являются (дБ/км )/( г/м³).

Чтобы вычислить общее ослабление для узкополосных сигналов вдоль пути, функция умножает конкретное ослабление на R длины пути. Общее ослабление _{Lc = Rγc}.

Можно применить модель ослабления к широкополосным сигналам. Сначала разделите широкополосный сигнал на частотные поддиапазоны и примените узкополосное ослабление к каждому поддиапазону. Затем суммируйте все ослабленные поддиапазонные сигналы в полный ослабленный сигнал.

Модель ослабления осадков

Эта модель вычисляет ослабление сигналов, которые распространяются через области осадков. Затухание дождя является доминирующим механизмом затухания и может варьироваться от места к месту и от года к году.

Электромагнитные сигналы ослабляются при распространении через область осадков. Ослабление осадков вычисляется согласно модели осадков МСЭ Рекомендация ITU-R P.838-3: Специфическая модель ослабления для дождя для использования в методах предсказания. Модель вычисляет удельное ослабление (ослабление на километр) сигнала как функцию скорости осадков, частоты сигнала, поляризации и угла возвышения пути. Конкретное ослабление, ɣ R, моделируется как закон степени относительно скорости дождя

$γ_{R} = k R^{α},$

где R - темп дождя. Модули указаны в мм/ч. k параметра и экспонента α зависят от частоты, состояния поляризации и угла возвышения пути сигнала. Специфическая модель ослабления действительна для частот от 1 до 1000 ГГц.

Чтобы вычислить общее ослабление для узкополосных сигналов вдоль пути, функция умножает конкретное ослабление на эффективное расстояние распространения, d _eff. Затем общее ослабление составляет L = d _eff γ R.

Эффективное расстояние является геометрическим расстоянием, d, умноженным на масштабный коэффициент

$r = \frac{1}{0.477 d^{0.633} R_{0.01}^{0.073 α} f^{0.123} - 10.579 (1 - \exp (- 0.024 d))}$

где f - частота. Статья Рекомендация ITU-R P.530-17 (12/2017): Данные о распространении и методы предсказания, необходимые для проекта наземных систем видимости, представляют собой полное обсуждение для вычисления ослабления.

Скорость дождя, R, используемая в этих расчетах, является долгосрочной статистической скоростью дождя, R _0,01. Это уровень дождей, который превышает 0,01% времени. Расчет статистической скорости дождя обсуждается в Рекомендации ITU-R P.837-7 (06/2017): Характеристики осадков для моделирования распространения. В этой статье также объясняется, как вычислить ослабление для других процентов от значения 0,01%.

Обработка частоты поддиапазона

Обработка поддиапазона разлагает широкополосный сигнал на несколько поддиапазонов и применяет узкополосную обработку к сигналу в каждом поддиапазоне. Сигналы для всех поддиапазонов суммируются, чтобы сформировать выходной сигнал.

При использовании широкополосных объектов или блоков Системы частоты вы задаете количество поддиапазонов, N B, в которых можно разложить широкополосный сигнал. Центральные частоты и ширины поддиапазона автоматически вычисляются из общей полосы пропускания и количества поддиапазонов. Полная полоса частот центрируется на несущей или рабочей частоте, _fc. Общая полоса пропускания задается частотой дискретизации, _fs. Ширина поддиапазона частот составляет Δf = f с/ N В. Центральные частоты поддиапазонов

$f_{m} = {\begin{matrix} f_{c} - \frac{f_{s}}{2} + (m - 1) Δ f, N_{B} даже \\ f_{c} - \frac{(N_{B} - 1) f_{s}}{2 N_{B}} + (m - 1) Δ f, N_{B} странный \end{matrix}, m = 1, \dots, N_{B}$

Некоторые Системные объекты позволяют вам получить центральные частоты поддиапазона как выходные при запуске объекта. Возвращенные частоты поддиапазона упорядочены последовательно с упорядоченным расположением дискретного преобразования Фурье. Сначала появляются частоты выше несущей, далее указываются частоты ниже несущей.

Ссылки

[1] Proakis, J. Digital Communications. Нью-Йорк: McGraw-Hill, 2001.

[2] Skolnik, M. Introduction to Радиолокационные Системы, 3rd Ed. New York: McGraw-Hill.

[3] Основы распространения Saakian, A. Radio Wave. Norwood, MA: Artech House, 2011.

[4] Balanis, C. Advanced Engineering Electromagnetics. Нью-Йорк: Wiley & Sons, 1989.

[5] Rappaport, T. Wireless Communications: Principles and Practice, 2nd Ed New York: Prentice Hall, 2002.

[6] Сектор радиосвязи Международного объединения электросвязи. Рекомендация ITU-R P.676-10: Ослабление атмосферными газами. 2013.

[7] Сектор радиосвязи Международного объединения электросвязи. Рекомендация ITU-R P.840-6: Ослабление из-за облаков и тумана. 2013.

[8] Сектор радиосвязи Международного объединения электросвязи. Рекомендация ITU-R P.838-3: Специфическая модель ослабления для дождя для использования в методах предсказания. 2005.

Расширенные возможности

Генерация кода C/C + +
Сгенерируйте код C и C++ с помощью Coder™ MATLAB ®

Указания и ограничения по применению:

Смотрите Системные объекты в Генерации кода MATLAB (MATLAB Coder).

См. также

Функции

fogpl | fspl | gaspl | rainpl | rangeangle

Объекты

phased.FreeSpace | phased.LOSChannel | phased.WidebandBackscatterRadarTarget | phased.WidebandFreeSpace | phased.WidebandLOSChannel | twoRayChannel

Введенный в R2021a

Документация

widebandTwoRayChannel

Описание

Конструкция

Свойства

PropagationSpeed - Скорость распространения сигнала physconst('LightSpeed') (по умолчанию) | положительная скалярная величина

OperatingFrequency - Рабочая частота 300e6 (по умолчанию) | положительная скалярная величина

SpecifyAtmosphere - Включите модель атмосферного ослабления false (по умолчанию) | true

Temperature - Температура окружающей среды 15 (по умолчанию) | скаляр с реальным значением

Зависимости

DryAirPressure - Атмосферное давление сухого воздуха 101.325e3 (по умолчанию) | положительный скаляр с реальным значением

Зависимости

WaterVapourDensity - Плотность паров воды в атмосфере 7.5 (по умолчанию) | положительный скаляр с реальным значением

Зависимости

LiquidWaterDensity - Плотность жидкой воды 0.0 (по умолчанию) | неотрицательный скаляр с реальным значением

Зависимости

RainRate - Норма осадков 0.0 (по умолчанию) | неотрицательной скаляром

Зависимости

SampleRate - Частота дискретизации сигнала 1e6 (по умолчанию) | положительная скалярная величина

NumSubbands - Количество обрабатывающих поддиапазонов 64 (по умолчанию) | положительное целое число

EnablePolarization - Включите поляризованные поля false (по умолчанию) | true

GroundReflectionCoefficient - Коэффициент отражения земли -1 (по умолчанию) | скалярный скаляр | комплексным вектором 1-байт- N строки

Зависимости

Зависимости

CombinedRaysOutput - Опция объединения двух лучей на выходе true (по умолчанию) | false

MaximumDistanceSource - Источник максимального одностороннего расстояния распространения 'Auto' (по умолчанию) | 'Property'

MaximumDistance - Максимальное одностороннее расстояние распространения 10000 (по умолчанию) | положительный скаляр с реальным значением

Зависимости

MaximumNumInputSamplesSource - Источник максимального количества выборок 'Auto' (по умолчанию) | 'Property'

Зависимости

MaximumNumInputSamples - Максимальное количество выборок входного сигнала 100 (по умолчанию) | положительное целое число

Зависимости

Методы

Примеры

Скалярный широкополосный сигнал, распространяющийся в двухлучевом канале

Сравнение широкополосного двухлучевого распространения канала к свободному пространству

Широкополосное поляризованное распространение поля в двухлучевом канале

Двухлучевое распространение широкополосной волны LFM с атмосферными потерями

Подробнее о

Двухлучевые пути распространения

Двухлучевое ослабление

Отражение земли и потери распространения

Модель ослабления атмосферного газа

Модель ослабления тумана и облака

Модель ослабления осадков

Обработка частоты поддиапазона

Ссылки

Расширенные возможности

Генерация кода C/C + + Сгенерируйте код C и C++ с помощью Coder™ MATLAB ®

См. также

Функции

Объекты

Документация по Radar Toolbox

Поддержка

`PropagationSpeed` - Скорость распространения сигнала
`physconst('LightSpeed')` (по умолчанию) | положительная скалярная величина

`OperatingFrequency` - Рабочая частота
`300e6` (по умолчанию) | положительная скалярная величина

`SpecifyAtmosphere` - Включите модель атмосферного ослабления
`false` (по умолчанию) | `true`

`Temperature` - Температура окружающей среды
`15` (по умолчанию) | скаляр с реальным значением

`DryAirPressure` - Атмосферное давление сухого воздуха
`101.325e3` (по умолчанию) | положительный скаляр с реальным значением

`WaterVapourDensity` - Плотность паров воды в атмосфере
`7.5` (по умолчанию) | положительный скаляр с реальным значением

`LiquidWaterDensity` - Плотность жидкой воды
`0.0` (по умолчанию) | неотрицательный скаляр с реальным значением

`RainRate` - Норма осадков
`0.0` (по умолчанию) | неотрицательной скаляром

`SampleRate` - Частота дискретизации сигнала
`1e6` (по умолчанию) | положительная скалярная величина

`NumSubbands` - Количество обрабатывающих поддиапазонов
`64` (по умолчанию) | положительное целое число

`EnablePolarization` - Включите поляризованные поля
`false` (по умолчанию) | `true`

`GroundReflectionCoefficient` - Коэффициент отражения земли
`-1` (по умолчанию) | скалярный скаляр | комплексным вектором 1-байт- N строки

`CombinedRaysOutput` - Опция объединения двух лучей на выходе
`true` (по умолчанию) | `false`

`MaximumDistanceSource` - Источник максимального одностороннего расстояния распространения
`'Auto'` (по умолчанию) | `'Property'`

`MaximumDistance` - Максимальное одностороннее расстояние распространения
`10000` (по умолчанию) | положительный скаляр с реальным значением

`MaximumNumInputSamplesSource` - Источник максимального количества выборок
`'Auto'` (по умолчанию) | `'Property'`

`MaximumNumInputSamples` - Максимальное количество выборок входного сигнала
`100` (по умолчанию) | положительное целое число

Генерация кода C/C + +
Сгенерируйте код C и C++ с помощью Coder™ MATLAB ®