Дискретное преобразование Фурье с алгоритмом Гертцеля второго порядка
Оцените частоты тонального сигнала, сгенерированного нажатием кнопки 1 на телефонной клавиатуре.
Число 1 выдает тональный сигнал с частотами 697 и 1209 Гц. Сгенерируйте 205 выборок тонального сигнала со скоростью дискретизации 8 кГц.
Fs = 8000; N = 205; lo = sin(2*pi*697*(0:N-1)/Fs); hi = sin(2*pi*1209*(0:N-1)/Fs); data = lo + hi;
Используйте алгоритм Гертцеля, чтобы вычислить дискретное преобразование Фурье (DFT) тонального сигнала. Выберите индексы, соответствующие частотам, используемым для генерации чисел от 0 до 9.
f = [697 770 852 941 1209 1336 1477]; freq_indices = round(f/Fs*N) + 1; dft_data = goertzel(data,freq_indices);
Постройте график величины ДПФ.
stem(f,abs(dft_data)) ax = gca; ax.XTick = f; xlabel('Frequency (Hz)') ylabel('DFT Magnitude')
Сгенерируйте шумный косинус с частотными составляющими на частотах 1,24 кГц, 1,26 кГц и 10 кГц. Задайте частоту дискретизации 32 кГц. Сбросьте генератор случайных чисел для воспроизводимых результатов.
rng default Fs = 32e3; t = 0:1/Fs:2.96; x = cos(2*pi*t*10e3) + cos(2*pi*t*1.24e3) + cos(2*pi*t*1.26e3) ... + randn(size(t));
Сгенерируйте вектор частоты. Используйте алгоритм Гертцеля, чтобы вычислить ДПФ. Ограничьте область значений частот в диапазоне от 1,2 до 1,3 кГц.
N = (length(x)+1)/2; f = (Fs/2)/N*(0:N-1); indxs = find(f>1.2e3 & f<1.3e3); X = goertzel(x,indxs);
Постройте график среднего квадратного спектра, выраженного в децибелах.
plot(f(indxs)/1e3,mag2db(abs(X)/length(X))) title('Mean Squared Spectrum') xlabel('Frequency (kHz)') ylabel('Power (dB)') grid
Сгенерируйте двухканальный сигнал, дискретизированный на частоте 3,2 кГц в течение 10 секунд и встроенный в белый Гауссов шум. Первый канал сигнала является синусоидой 124 Гц. Второй канал является комплексной экпонентой с частотой 126 Гц. Измените форму сигнала на трехмерный массив таким образом, чтобы ось времени проходила вдоль третьей размерности.
fs = 3.2e3; t = 0:1/fs:10-1/fs; x = [cos(2*pi*t*124);exp(2j*pi*t*126)] + randn(2,length(t))/100; x = permute(x,[3 1 2]); size(x)
ans = 1×3
1 2 32000
Вычислите дискретное преобразование Фурье сигнала с помощью алгоритма Гертцеля. Ограничьте область значений частот от 120 Гц до 130 Гц.
N = (length(x)+1)/2; f = (fs/2)/N*(0:N-1); indxs = find(f>=120 & f<=130); X = goertzel(x,indxs,3);
Постройте график величины дискретного преобразования Фурье, выраженного в децибелах.
plot(f(indxs),mag2db(abs(squeeze(X)))) xlabel('Frequency (Hz)') ylabel('DFT Magnitude (dB)') grid
Алгоритм Гертцеля реализует дискретное X преобразования Фурье (k) как свертку входного N x (n), n = 0, 1,..., N - 1 с импульсной характеристикой
где u (n), модуль последовательность шагов, равна 1 для n ≥ 0 и 0 в противном случае. k не обязательно должно быть целым числом. На частоте f = k f s/ N, где f s - частота дискретизации, преобразование имеет значение
где
и x (N) = 0. Z-преобразование импульсной характеристики
с этой прямой формой II реализации:
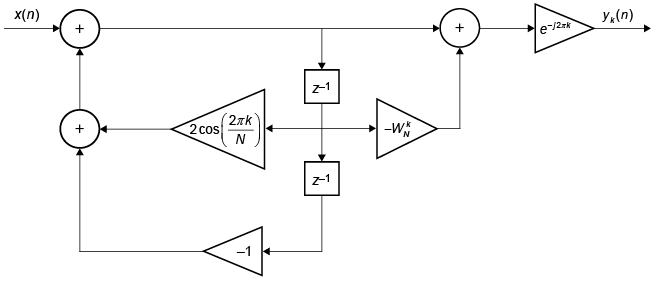
Сравните выходные данные goertzel к результату прямой реализации алгоритма Гертцеля. Для входного сигнала используйте щебет, дискретизированный на частоте 50 Гц в течение 10 секунд и встроенный в белый Гауссов шум. Частота щебета увеличивается линейно с 15 Гц до 20 Гц во время измерения. Вычислите дискретное преобразование Фурье на частоте, которая не является целым числом, кратным f s/ N. При вызовеgoertzel, имейте в виду, что MATLAB® векторы выполняются от 1 до N вместо от 0 до N - 1. Результаты согласны с высокой точностью.
fs = 50; t = 0:1/fs:10-1/fs; N = length(t); xn = chirp(t,15,t(end),20)+randn(1,N)/100; f0 = 17.36; k = N*f0/fs; ykn = filter([1 -exp(-2j*pi*k/N)],[1 -2*cos(2*pi*k/N) 1],[xn 0]); Xk = exp(-2j*pi*k)*ykn(end); dft = goertzel(xn,k+1); df = abs(Xk-dft)
df = 4.3634e-12
Можно также вычислить ДПФ с:
fft: менее эффективный, чем алгоритм Гертцеля, когда вам нужен только ДПФ на нескольких частотах. fft является более эффективным, чем goertzel когда вам нужно вычислить преобразование на более чем лог2 частотах N, где N - длина входного сигнала.
czt: czt вычисляет Z-преобразование ЛЧМ входного сигнала на круговом или спиральном контуре и включает ДПФ в качестве особого случая.
[1] Беррус, К. Сидни и Томас У. Паркс. Алгоритмы DFT/FFT и свертки: теория и реализация. Нью-Йорк: John Wiley & Sons, 1985.
[2] Проакис, Джон Г. и Димитрис Г. Манолакис. Цифровая обработка сигналов: принципы, алгоритмы и приложения. 3-е издание. Upper Saddle River, NJ: Prentice Hall, 1996.
[3] Сисель, Петр и Павел Раджмич. «Алгоритм Гертцеля, обобщенный на нецелочисленные множители основной частоты». Журнал EURASIP о усовершенствованиях в обработке сигналов. Том 2012, № 1, декабрь 2012, стр. 56-1-56-8. https://doi.org/10.1186/1687-6180-2012-56.