Симуляция модели динамической системы позволяет вам получить представление о поведении предлагаемой разработки системы без длительного процесса фактического создания системы. Концепции в этой теме обеспечивают контекст для понимания того, как управлять симуляцией модели с Simulink® программные инструменты.
Компиляция является процессом Simulink, где block diagram переведено во внутреннее представление, которое взаимодействует с движком Simulink.
Нет наборов дифференциальных уравнений уровня модели, которые решаются численно как единое целое. Вместо этого уравнения уровня модели соответствуют отдельным блочным уравнениям, которые решаются численно в определенном порядке.
Функциональность одного блока определяется несколькими уравнениями. Эти уравнения представлены как блочные методы. Эти методы блока оцениваются (выполняются) во время выполнения блока схемы. Оценка этих блочных методов выполняется в цикле симуляции, где каждый цикл через цикл симуляции представляет оценку блока в заданную точку времени. Общие методы блока включают:
Производная - вычисляет производные непрерывных состояний блока в текущем временном шаге, учитывая входы блока и значения состояний на предыдущем временном шаге.
Обновление - вычисляет значение дискретных состояний блока в текущем временном шаге, учитывая его входы в текущем временном шаге и его дискретные состояния в предыдущем временном шаге.
Выход - вычисляет выходы блока, заданные его входы в текущем временном шаге и его состояния на предыдущем временном шаге.

В дополнение к блочным методам предусмотрен набор методов, которые вычисляют свойства модели и ее выходы. Программа Simulink аналогично вызывает эти методы во время симуляции, чтобы определить свойства модели и ее выходы. Методы модели обычно выполняют свои задачи, вызывая блочные методы того же типа. Например, метод model Outputs вызывает методы Outputs блоков, которые он содержит в порядке, заданном моделью, чтобы вычислить его выходы. Метод model Derivatives аналогично вызывает методы Derivatives блоков, которые он содержит, чтобы определить производные его состояний.
Смотрите также: Фазы симуляции в динамических системах.
Коллбэки - это выражения MATLAB, которые выполняются в ответ на определенное действие моделирования. Simulink предоставляет параметры коллбэка модели, блока и порта, которые идентифицируют определенные виды действий моделирования. Вы предоставляете код для параметров коллбэка. Simulink выполняет код коллбэка, когда происходит связанное действие моделирования.
Коллбэки модели включают:
PreloadFcn - Выполняется перед загрузкой модели. Например, можно предоставить код, который загружает значения переменных, используемые моделью, в рабочее пространство MATLAB.
См. Модель коллбэков.
Блоки коллбэка параметры включают:
OpenFcn - Выполняется, когда вы открываете блок Subsystem.
LoadFcn - Выполняется после загрузки схемы. Для блоков Subsystem также выполните параметры коллбэка блоков в Subsystem блоке.
Коллбэк порта:
ConnectionCallback - Выполнять код каждый раз, когда изменяется связь порта.
См. Раздел «Коллбэки»
Порядок выполнения является последовательностью, в которой методы выхода блоков вызываются после оценки прямого сквозного соединения каждого входного порта. Чтобы отобразить порядок выполнения, на вкладке Debug, выберите Information Overlays > Execution Order.
В следующей модели сначала запускается выход блока Integrator, а затем цикл блоков, соединенный с входом блока Integrator. Отсутствующие номера выполнения в последовательности обычно связаны с скрытыми буферными блоками.
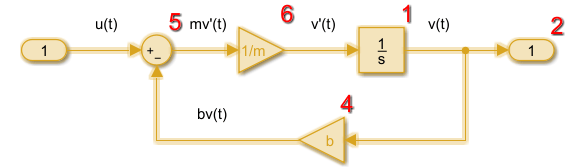
Смотрите также: Управление и отображение порядка выполнения, Фазы симуляции в динамических системах.
Simulation - процесс после компиляции модели, в котором выходы блочного метода и состояния вычисляются в последовательных временных шагах в заданной временной области значений с помощью численного решателя.
Во время каждого цикла симуляции Simulink вычисляет Δt для определения временного шага t(k+1) = t(k) + Δt. Размер Δt основывается на оценочной ошибке между моделируемым решением и фактическим решением. В конце симуляции результаты данных даются как векторы [t, X, Y] для времени, состояния и выхода на каждом временном шаге.
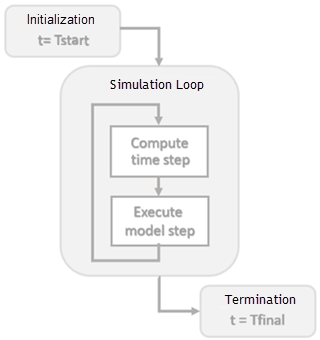
Смотрите также: Фазы симуляции в динамических системах, Моделирование модели интерактивно, Симуляция ускорения.
Решатель находит приблизительное решение для набора уравнений модели. Simulink использует установленные числовые решатели для этой задачи.
Размер шага решателя может быть фиксированным или переменным:
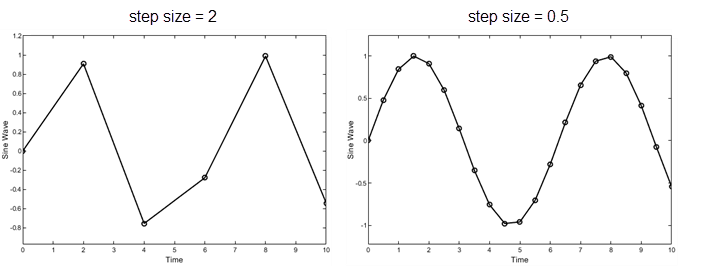
Фиксированный шаг - Временной шаг T(k+1) = T(k) + Δt где Δt является постоянным. Если размер шага слишком велик, результаты симуляции могут иметь большую ошибку. В следующем примере размер шага 2 искажает форму синусоиды сигнала. Можно задать размер временного шага в случае решателей с фиксированным шагом, или решатель может автоматически определить размер шага в случае решателей с переменным шагом.
Переменный шаг - Переменные переменного шага итератируют, чтобы достичь решения, основанного на допуске ошибки. Временной шаг T(k+1) = T(k) + Δtₖ где Δtₖ изменяется с одного шага симуляции на следующий в зависимости от предполагаемой ошибки. Меньшие временные шаги увеличивают точность результатов симуляции. Чтобы минимизировать рабочую нагрузку расчета, решатель с переменным шагом выбирает наибольший размер шага, сопоставимый с достижением общего уровня точности, заданного допуском ошибок, и наблюдением пересечений нулем. Это гарантирует, что все состояния модели вычисляются с точностью, заданной пользователем.
Выбор метода решателя зависит от природы уравнений модели. Метод Эйлера является простым числовым решателем, который вычисляет следующее значение y при помощи наклона (y') тангенса, линия для y. Если y - функция, которая интегрирует линейную функцию x с наклоном 1, y' = x, и численный решатель использует следующие уравнения.
x[n+1] = x[n] + Δt*1 y[n+1] = y[n] + Δt*x[n+1]
Уменьшение размера шага увеличивает точность результатов. но это увеличивает время для выполнения симуляции. В следующем примере размер шага 2 показывает ошибку около 20 процентов через 10 секунд, в то время как размер шага 0.5 приводит к результату, который ближе к фактическому решению.