Extremum sequing control (ESC) является адаптивным алгоритмом управления без моделей в реальном времени, который полезен для адаптации к неизвестной динамике системы и неизвестным отображениям из параметров управления в целевую функцию. Можно использовать extremum поиск для решения статических задач оптимизации и оптимизации параметров динамических систем.
Алгоритм поиска экстремума использует следующие этапы, чтобы настроить значение параметров.
Модуляция - Возмущает значение оптимизируемого параметра с помощью синусоидального сигнала с низкой амплитудой.
Отклик системы - оптимизируемая система реагирует на возмущения параметра. Эта реакция вызывает соответствующее изменение значения целевой функции.
Демодуляция - умножение сигнала целевой функции на синусоиду с той же частотой, что и сигнал модуляции. Этот каскад включает дополнительный фильтр высоких частот для удаления смещения из сигнала целевой функции.
Обновление параметра - обновляйте значение параметров путем интегрирования демодулированного сигнала. Значение параметров соответствует состоянию интегратора. Этот каскад включает в себя дополнительный lowpass для удаления высокочастотного шума из демодулированного сигнала.
Simulink® Программное обеспечение Control Design™ реализует этот алгоритм с помощью блока Extremum Seeking Control. Для примеров контроля за экстремумом смотрите:
Чтобы продемонстрировать поиск экстремума, рассмотрите следующую статическую задачу оптимизации.
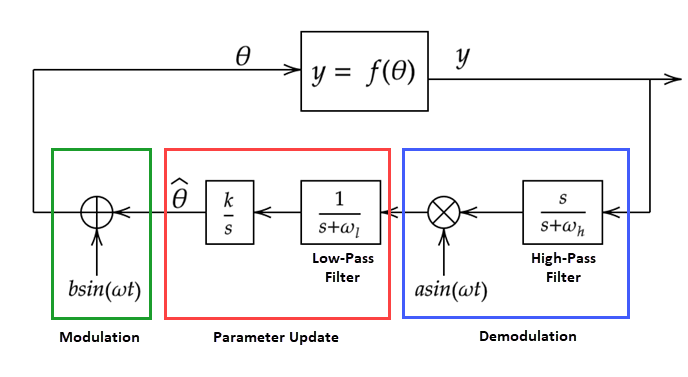
Здесь:
- предполагаемое значение параметров.
θ является сигналом модуляции
y = f (θ) является выходом функции, который максимизируется, то есть целевой функцией.
ω - частота принудительной модуляции и сигналов демодуляции.
b· sin (ωt) является сигналом модуляции.
a· sin (ωt) является сигналом демодуляции.
ωl - частота отключения низкочастотного фильтра.
ωh - частота отключения высокочастотного фильтра.
k является скоростью обучения.
Оптимальное значение параметров, θ*, происходит при максимальном значении f (θ).
Чтобы оптимизировать несколько параметров, вы используете отдельный цикл настройки для каждого параметра.
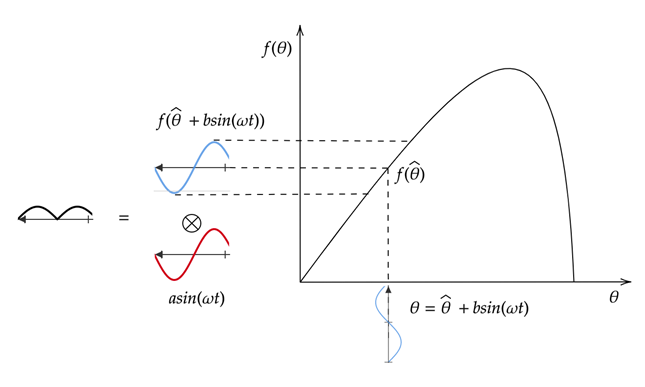
Следующий рисунок демонстрирует экстремум, ищущий увеличивающийся фрагмент кривой целевой функции. Модулированный θ сигнала является суммой текущего оцененного параметра и сигнала модуляции. Применение f (θ) производит возмущенную целевую функцию с той же фазой, что и сигнал модуляции. Умножение возмущенной целевой функции на сигнал демодуляции генерирует положительный сигнал. Интегрирование этого сигнала увеличивает значение θ, что перемещает его ближе к пику целевой функции.
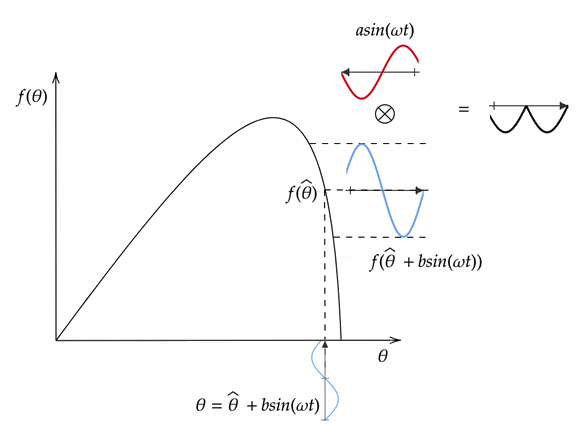
Следующий рисунок демонстрирует экстремум, ищущий уменьшающийся фрагмент кривой целевой функции. В этом случае применение f (θ) создает возмущенную целевую функцию, которая на 180 степени превышает фазу pf от сигнала модуляции. Умножение на сигнал демодуляции генерирует отрицательный сигнал. Интегрирование этого сигнала уменьшает значение θ, что перемещает его ближе к пику целевой функции.
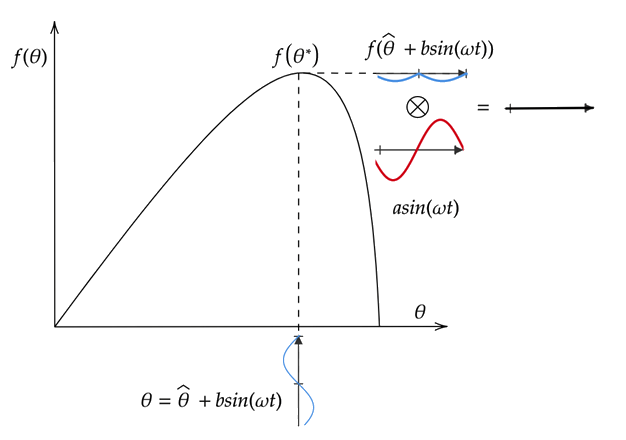
Следующее изображение демонстрирует экстремум, ищущий плоский фрагмент кривой целевой функции, то есть фрагмент кривой, близкую к максимуму. В этом случае применение f (θ) создает почти нулевую возмущенную целевую функцию. Интегрирование этого сигнала существенно не изменяет значение θ, которое уже близко к его оптимальной θ*.
Экстремум, ищущий оптимизацию динамической системы, происходит так же, как и статическая оптимизация. Однако в этом случае θ параметра влияет на выход зависящей от времени динамической системы. Целевая функция, которая будет максимизирована, вычисляется из выхода. Следующий рисунок показывает общий цикл настройки для динамической системы.
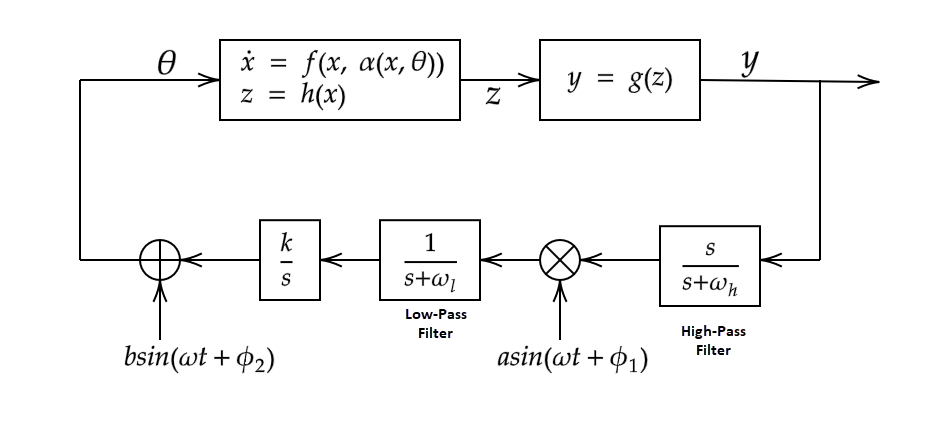
Здесь:
- функция состояния динамической системы.
z = h (x) является выходом динамической системы.
y = g (z) является целевой функцией, выведенной из выхода динамической системы.
ϕ 1 является фазой сигнала демодуляции.
ϕ 2 является фазой сигнала модуляции.
При разработке контроллера поиска экстремума примите во внимание следующие рекомендации.
Убедитесь, что динамика системы находится в самой быстрой временной шкале, частоты принуждения - в среднем временной шкале, а частоты отключения фильтра - в самой медленной временной шкале.
Задайте амплитуду для сигнала демодуляции, которая намного больше, чем амплитуда сигнала модуляции (a ≫ b).
Выберите углы фазы для сигналов модуляции и демодуляции, таких что cos (ϕ 1 - ϕ 2) > 0.
При настройке нескольких параметров частота принудительной настройки для каждого цикла настройки должна быть различной.
Попробуйте разработать свою систему без высокочастотных и низкочастотных фильтров. Если эффективность не удовлетворительна, можно рассмотреть возможность добавления одного или обоих фильтров.
[1] Ариюр, Картик Б., и Мирослав Крстич. Оптимизация в реальном времени с помощью Extremum Searning Control. Hoboken, NJ: Wiley Interscience, 2003.