В Response Optimizer можно задать следующие ограничения на Simulink® параметры модели, которые заданы как переменные:
Monotonic Variable - Наложение требования к монотонным ограничениям на переменную
Smoothness Constraint - наложение верхней границы на величину градиента переменной
Function Matching - Задайте линейное или квадратичное ограничение соответствия функций
Vector Property - Задание требования к свойству вектора
Relational Constraint - Наложение реляционного ограничения между двумя переменными
Для получения информации о том, как задать параметр модели как переменную, смотрите Добавить параметры модели как Переменные для Оптимизации. После того, как вы задаете ограничения, можно увидеть, удовлетворены ли требования путем оптимизации конструктивных переменных. Для получения дополнительной информации смотрите Задать опции оптимизации.
Вы можете наложить монотонное ограничение на переменный проект в модели Simulink. Например, ограничьте переменную монотонным увеличением. Переменная может быть векторным, матричным или многомерным массивом, который является параметром в вашей модели, таким как точки останова интерполяционной таблицы.
Чтобы указать требование:
В Response Optimizer, в New меню, выберите Monotonic Variable.

В диалоговом окне «Создание требования» задайте требование.
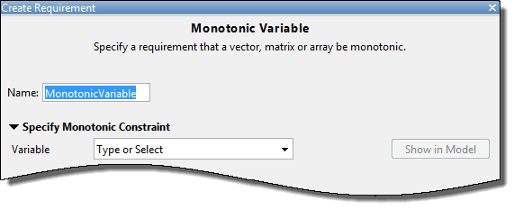
Укажите имя требования в Name.
Укажите имя переменной в Variable. Переменная должна быть векторным, матричным или многомерным массивом данных double или single.
Можно ввести имя переменного нескаляра или выбрать переменную из выпадающего списка. Список заполняется всеми нескалярными переменными в вашей модели. Чтобы выбрать подмножество массива или матричной переменной V, введите выражение. Для примера задайте Variable следующим V(1,:) для использования первой строки переменной. Чтобы использовать числовое нескалярное поле x структуры S, тип S.x. Вы не можете использовать математические выражения, такие как a + b.
Иногда модели имеют параметры, которые не определены явно в самой модели. Для примера - коэффициент усиления k может быть определено в MATLAB® рабочая область как k = a + b, где a и b не определены в модели, но k используется. Чтобы добавить эти независимые параметры как переменные в Response Optimizer, смотрите Добавить параметры модели как Переменные для Оптимизации.
Задайте монотонность для каждой размерности переменной.
После выбора переменной диалоговое окно обновляется, чтобы показать Dimension 1 к Dimension n, соответствующим n размерностям переменной. Для примера - для 2-мерной переменной K размера 3 на 5 диалоговое окно обновляется, как показано на рисунке.
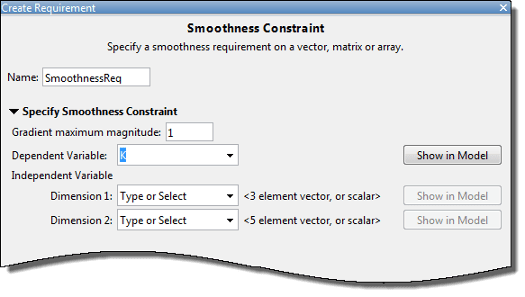
Задайте монотонность для первой размерности в Dimension 1 и для nth-размерность в Dimension n как один из следующих опций:
Strictly increasing - Каждый элемент переменной больше, чем предыдущий элемент в этом измерении.
Increasing - Каждый элемент переменной больше или равен предыдущему элементу в этом измерении.
Decreasing - Каждый элемент переменной меньше или равен предыдущему элементу в этом измерении.
Strictly decreasing - Каждый элемент переменной меньше, чем предыдущий элемент в этом измерении.
Not constrained - Нет ограничений между элементами переменной в этой размерности.
(Необязательно) Чтобы создать итерационный график, который показывает рассчитанное значение требования для каждой итерации оптимизации, выберите Create Plot. График заполняется при выполнении оптимизации. На график показано рассчитанное значение потребности, соответствующее каждой размерности переменной. Положительное значение указывает, что требование было нарушено.
Нажмите OK.
Новая переменная с заданным именем требования появится в области Data приложения Response Optimizer.
Можно наложить верхнюю границу на величину градиента переменной в модели Simulink. Переменная может быть векторным, матричным или многомерным массивом, который является параметром в вашей модели, таким как данные интерполяционной таблицы. Например, рассмотрите контроллер двигателя автомобиля, чей коэффициент усиления изменяется при различных условиях работы, определяемых скоростью автомобиля. Можно использовать ограничение, связанное с градиентом, чтобы ограничить скорость, с которой коэффициент усиления контроллера изменяется на модуль изменения скорости транспортного средства.
Для N -мерной переменной F это функция независимых переменных x1..., xNградиентная величина определяется как:
Чтобы вычислить величину градиента, программа вычисляет частную производную в каждой размерности, вычисляя различие между последовательными F данные в этой размерности и деление на интервал между данными в этой размерности. Вы задаете F и интервал между данными. Программа проверяет, меньше ли или равна градиентная величина данных переменной заданной границы. Если градиентная величина данных больше необходимой границы, данные переменной не сглаживаются.
Чтобы указать требование:
В Response Optimizer, в New раскрывающемся списке, выберите Smoothness Constraint.

В диалоговом окне «Создание требования» задайте требование.
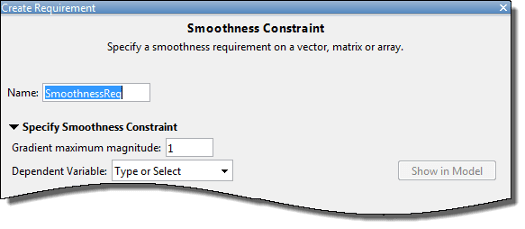
Укажите имя требования в Name.
Задайте градиентную величину, связанную как неотрицательную конечную действительную скаляру в Gradient maximum magnitude.
Задайте переменную F что вы хотите навязать требование в Dependent Variable. Переменная должна быть векторным, матричным или многомерным массивом данных double или single. Переменная должна быть параметром в вашей модели или константой, которую вы вводите.
Можно ввести имя переменного нескаляра или константы или выбрать переменную из выпадающего списка. Список заполняется всеми нескалярными переменными в вашей модели. Чтобы выбрать подмножество массива или матричной переменной V, введите выражение. Для примера задайте Variable следующим V(1,:) для использования первой строки переменной. Чтобы использовать числовое нескалярное поле x структуры S, тип S.x. Вы не можете использовать математические выражения, такие как a + b.
Иногда модели имеют параметры, которые не определены явно в самой модели. Для примера - коэффициент усиления k может быть определено в рабочем пространстве MATLAB следующим образом k = a + b, где a и b не определены в модели, но k используется. Чтобы добавить эти независимые параметры как переменные в Response Optimizer, смотрите Добавить параметры модели как Переменные для Оптимизации.
Задайте интервал между точками Dependent Variable данных в каждой размерности в Independent Variable.
После выбора Dependent Variable диалоговое окно обновляется, чтобы показать, Dimension 1 Dimension n, соответствующие n размерностям зависимой переменной. Для примера - для 1-мерной переменной Kдиалоговое окно обновляется как показано на рисунке.
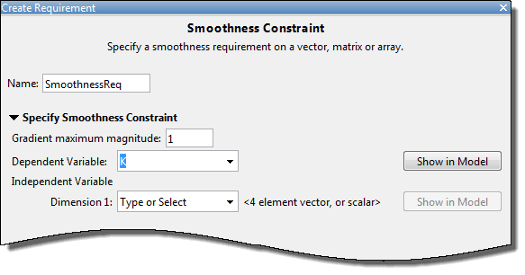
Первая размерность задаёт интервал вниз по зависимым строкам данных переменных, а второй интервал между столбцами. N-й размерность задает интервал вдоль N-го размерности зависимых переменных данных. Можно задать независимые переменные в каждой размерности как скаляры или векторы.
Скаляры - задайте интервал между зависимыми переменными данными F в соответствующей размерности как ненулевой скаляр. Например, предположим, что Dependent Variable является двумерным, и интервал между данными в первой размерности 5 и во втором измерении это 2. В Independent Variable разделе задайте Dimension 1 следующим 5 и Dimension 2 как 2.
Векторы - Задайте координаты F данные в соответствующей размерности как вещественные, числовые, монотонные векторы. Программа использует координаты, чтобы вычислить интервал между зависимыми переменными точками данных в соответствующей размерности. Длина вектора должна совпадать с длиной F в соответствующей размерности. Вы не должны задавать координаты с равномерным интервалом. Например, предположим, что F является двумерным, и длина данных в первом и вторых измерениях 3 и 5, соответственно. Координаты данных в первой размерности [1 2 3]. Во втором измерении интервал неоднороден, и координаты данных [1 2 10 20 30]. В Independent Variable разделе задайте Dimension 1 следующим [1 2 3] и Dimension 2 как [1 2 10 20 30].
Можно также задать независимые переменные, введя имя переменной или выбрав переменную из выпадающего списка. Список заполняется всеми переменными в вашей модели, которые имеют соответствующий размер. Чтобы выбрать подмножество массива или матричной переменной V, введите выражение. Для примера задайте как V(1,:) для использования первой строки переменной. Использование числового поля x структуры S, тип S.x. Вы не можете использовать математические выражения, такие как a + b.
(Необязательно) Чтобы создать итерационный график, который показывает рассчитанное значение требования для каждой итерации оптимизации, выберите Create Plot. График заполняется при выполнении оптимизации. Положительное значение указывает, что требование было нарушено.
Нажмите OK.
Новая переменная с заданным именем требования появится в области Data Response Optimizer.
В приложении можно ограничить значения переменной, чтобы они совпадали с линейной или квадратичной функцией. Переменная может быть вектором, матрицей или многомерным массивом, который является параметром в вашей модели, таким как данные интерполяционной таблицы в вашей модели. Чтобы указать требование:
В Response Optimizer из выпадающего списка New выберите Function Matching.

В диалоговом окне «Создание требования» задайте требование. Новое требование с именем, заданным в Name, появляется в Requirements области приложения.
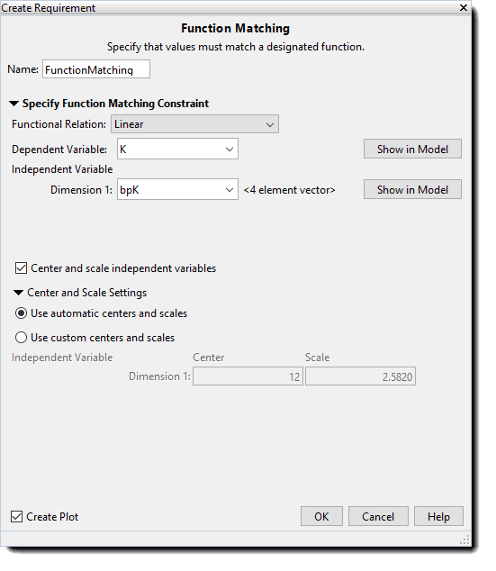
Задайте функцию, которая будет совпадать. Для этого установите Functional Relation одно из следующих значений:
Linear - Данные из переменных V соответствуют линейной функции. Для примера, для двумерной переменной с независимыми переменными, X1 и X2линейная функция имеет вид:
Программа вычисляет коэффициенты аппроксимации a0, a1, и a2 а затем вычисляет сумму квадратов ошибки между данными и линейной функцией.
Quadratic with no cross-terms - Данные подгоняются к квадратичной функции без перекрестных членов. Для двумерной переменной чистая квадратичная функция имеет вид:
Quadratic with all cross-terms - Переменные данные подгоняются к квадратичной функции, которая включает в себя перекрестные условия. Для двумерной переменной квадратичная функция имеет вид:
Если переменная одномерна, перекрестных терминов нет, и поэтому расчеты те же, что и когда Functional relation Quadratic with no cross-terms.
Задайте переменную V к которому необходимо применить требование в Dependent Variable. Переменная должна быть векторным, матричным или многомерным массивом данных double или single это параметр в вашей модели.
Введите имя переменного нескаляра или выберите переменную из выпадающего списка. Список заполняется всеми нескалярными переменными в вашей модели. Чтобы увидеть, где выбранная переменная используется в вашей модели, нажмите Show in Model. Чтобы выбрать подмножество массива или матричной переменной A, введите выражение. Для примера задайте A(1,:) для использования первой строки переменной. Чтобы использовать числовое нескалярное поле x структуры S, тип S.x. Вы не можете использовать математические выражения, такие как a + b.
Иногда модели имеют параметры, которые не определены явно в самой модели. Для примера - коэффициент усиления k может быть определено в рабочем пространстве MATLAB следующим образом k = a + b, где a и b не определены в модели, но k используется. Чтобы добавить эти независимые параметры как проект переменные в приложении, смотрите Добавить параметры модели как Переменные для Оптимизации.
Задайте независимые векторы переменных, используемые для вычисления функции в Independent Variable. Независимые переменные заданы как вещественные, числовые, монотонные векторы.
Количество независимых переменных должно равняться количеству размерностей зависимой переменной V. Для примера вы задаете две независимые переменные, когда V является матрицей и использует три независимые переменные при V является трехмерным. Первый независимый вектор переменной задает координаты, идущие вниз по строкам V, и второй независимый вектор переменной задает координаты, проходящие через столбцы V. Nth независимый вектор переменной задает координаты вдоль nth размерность V. Количество элементов в каждом независимом векторе переменной должно совпадать с размером V в соответствующей размерности. Независимые векторы переменных должны быть монотонно увеличивающимися или уменьшающимися.
Можно также задать независимые переменные, введя имя переменной или выбрав переменную из выпадающего списка. Список заполняется всеми переменными в вашей модели, которые имеют соответствующий размер. Чтобы выбрать подмножество массива или матричной переменной A, введите выражение. Для примера задайте A(1,:) для использования первой строки переменной. Использование числового поля x структуры S, тип S.x. Вы не можете использовать математические выражения, такие как a + b. Чтобы использовать вектор с равными интервалами, выберите [1 2 ...N] из раскрывающегося меню.
Укажите, нужно ли центрировать и масштабировать независимые переменные. Когда вы выбираете опцию Center and scale independent variables, заданные вами независимые векторы переменной делятся на значение шкалы после вычитания центрального значения. Центрирование может улучшить численное обусловленность, когда один или несколько независимых векторов переменной имеют среднее значение, которое отличается от 0 несколькими порядками величины. Масштабирование может улучшить численное обусловление, когда независимые переменные векторы отличаются друг от друга на несколько порядков величин.
Чтобы задать центр и шкалу значений для каждой независимой переменной, разверните Center and Scale Settings раздел и выберите один из следующих:
Use automatic centers and scales - значения центра и шкалы являются средним и стандартным отклонением для каждой независимой переменной. Использование среднего и стандартного значений отклонения для центрирования и масштабирования независимых переменных является опцией по умолчанию.
Use custom centers and scales - Задайте значения Center и Scale для каждой независимой переменной. Независимые векторы переменной делятся на соответствующее Scale значение после вычитания значения, заданного вами в Center.
(Необязательно) Выберите опцию Create Plot, чтобы создать итерационный график, который показывает рассчитанное значение требования для каждой итерации оптимизации. Программа вычисляет сигнал ошибки, который является различием между зависимыми данными переменной и заданной функцией независимых переменных. Сумма квадратов этой ошибки строится при выполнении оптимизации. Положительное значение указывает, что требование было нарушено, и 0 значение указывает, что требование удовлетворено. Чем ближе значение, тем 0, чем лучше соответствие между функцией и зависимыми переменными данными.
Закройте диалоговое окно «Создание требования».
Требование, созданное в Requirements области приложения, обновляется с заданными характеристиками.
Можно задать требование к свойству вектора, такому как среднее значение вектора. Вектор должен быть параметром в вашей модели. Чтобы указать требование:
В Response Optimizer, в New раскрывающемся списке, выберите Vector Property.

В диалоговом окне «Создание требования» задайте требование.
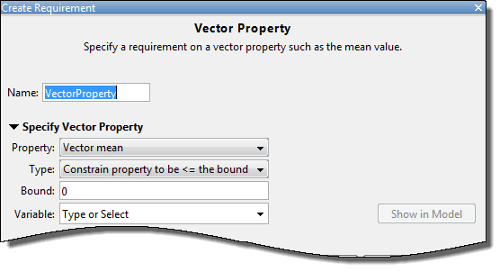
Укажите имя требования в Name.
Задайте свойство вектора в Property. Для вектора V с N элементами можно задать одно из следующих свойств:
Vector mean — mean (<reservedrangesplaceholder0>)
Vector median — median (<reservedrangesplaceholder0>)
Vector variance — variance (<reservedrangesplaceholder0>)
Vector inter-quartile range - Различие между 75-м и 25-м процентилями векторных значений.
Vector sum —
Vector sum of squares —
Vector sum of absolute values —
Vector minimum — min (<reservedrangesplaceholder0>)
Vector maximum — max (<reservedrangesplaceholder0>)
Задайте тип требования, которое вы хотите применить к свойству вектора в Type. Можно задать верхнюю или нижнюю границу свойства вектора или потребовать, чтобы свойство равнялось конкретному значению. Можно также принять решение максимизировать или минимизировать свойство вектора. Для примера, чтобы максимизировать среднее значение вашего вектора, задайте Property как Vector mean и Type как Maximize the property.
Задайте значение привязки, наложенной на свойство вектора в Bound. Задайте границу как конечное действительное скалярное значение. Для примера, если для переменного вектора V вы требуете mean(V) = 5, задайте Property следующим Vector mean, Type как Constrain property to be == the bound, и Bound как 5.
Укажите имя переменной в Variable. Переменная должна быть векторным, матричным или многомерным массивом данных double или single.
Можно ввести имя переменного нескаляра или выбрать переменную из выпадающего списка. Список заполняется всеми нескалярными переменными в вашей модели. Чтобы выбрать подмножество массива или матричной переменной V, введите выражение. Для примера задайте Variable следующим V(1,:) для использования первой строки переменной. Чтобы использовать числовое нескалярное поле x структуры S, тип S.x. Вы не можете использовать математические выражения, такие как a + b.
Иногда модели имеют параметры, которые не определены явно в самой модели. Для примера - коэффициент усиления k может быть определено в рабочем пространстве MATLAB следующим образом k = a + b, где a и b не определены в модели, но k используется. Чтобы добавить эти независимые параметры как переменные в Response Optimizer, смотрите Добавить параметры модели как Переменные для Оптимизации.
(Необязательно) Чтобы создать итерационный график, который показывает рассчитанное значение требования для каждой итерации оптимизации, выберите Create Plot. График заполняется при выполнении оптимизации. Положительное значение указывает, что требование было нарушено.
Нажмите OK.
Новая переменная с заданным именем требования появится в области Data приложения Response Optimizer.
Вы можете наложить требование реляционных ограничений на пару переменных в вашей модели Simulink. Для примера требуйте, чтобы a переменной всегда была больше, чем b переменной. Чтобы указать требование:
В Response Optimizer, в New раскрывающемся списке, выберите Relational Constraint.

В диалоговом окне «Создание требования» задайте требование.
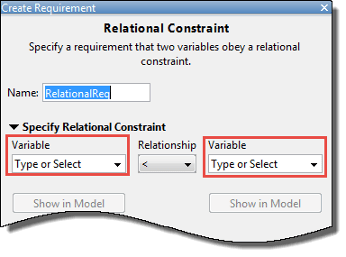
Укажите имя требования в Name.
Задайте имя двух переменных в Variable. Переменные могут быть векторами или массивами, но должны быть того же размера.
Введите имена двух переменных или выберите переменные из выпадающих списков. Списки заполняются всеми переменными в вашей модели. Чтобы увидеть, где выбранная переменная используется в вашей модели, нажмите Show in Model. Чтобы выбрать подмножество массива или матричной переменной V, введите выражение. Для примера задайте Variable следующим V(1,:) для использования первой строки переменной. Использование числового поля x структуры S, тип S.x. Вы не можете использовать математические выражения, такие как a + b.
Иногда модели имеют параметры, которые не определены явно в самой модели. Для примера - коэффициент усиления k может быть определено в рабочем пространстве MATLAB следующим образом k = a + b, где a и b не определены в модели, но k используется. Чтобы добавить эти независимые параметры как переменные в Response Optimizer, смотрите Добавить параметры модели как Переменные для Оптимизации.
Задайте отношение между элементами двух переменных как одно из следующего в Relationship:
'<' - Каждый элемент данных в первой переменной меньше, чем соответствующий элемент во второй переменной.
'<=' - Каждый элемент данных в первой переменной меньше или равен соответствующему элементу во второй переменной.
'>' - Каждый элемент данных в первой переменной больше, чем соответствующий элемент во второй переменной.
'>=' - Каждый элемент данных в первой переменной больше или равен соответствующему элементу во второй переменной.
'==' - Каждый элемент данных в первой переменной равен соответствующему элементу во второй переменной.
'~=' - Каждый элемент данных в первой переменной не равен соответствующему элементу во второй переменной.
(Необязательно) Чтобы создать итерационный график, который показывает рассчитанное значение требования для каждой итерации оптимизации, выберите Create Plot. График заполняется при выполнении оптимизации. На график показано рассчитанное значение потребности, соответствующее каждому элементу переменных. Интерпретация оцененного значения требования зависит от Type требования.
| Type | Оцененное значение требования | |
|---|---|---|
| Требование удовлетворено | Требование нарушено | |
'>' или '<' | Отрицательное число | Положительное число, или 0 если элементы равны |
'>=' или '<=' | Отрицательное число, или 0 если элементы равны | Положительное число |
'==' | 0 | Ненулевое число |
'~=' | 0 | 1 |
Нажмите OK.
Новая переменная с заданным именем требования появится в области Data приложения Response Optimizer.