resubLoss

Ошибка классификации путем реподституции

Синтаксис

L = resubLoss(obj) L = resubLoss(obj,Name,Value)

Описание

L = resubLoss(obj) возвращает потери реституции, означающие потери, рассчитанные для данных, которые fitcdiscr используется для создания obj.

L = resubLoss(obj,Name,Value) возвращает статистику потерь с дополнительными опциями, заданными одним или несколькими Name,Value аргументы в виде пар.

Входные параметры

расширить все

obj

Классификатор дискриминантного анализа, полученный с использованием fitcdiscr.

Аргументы в виде пар имя-значение

Задайте необязательные разделенные разделенными запятой парами Name,Value аргументы. Name - имя аргумента и Value - соответствующее значение. Name должны находиться внутри кавычек. Можно задать несколько аргументов в виде пар имен и значений в любом порядке Name1,Value1,...,NameN,ValueN.

`'LossFun'` - Функция потерь
`'mincost'` (по умолчанию) | `'binodeviance'` | `'classiferror'` | `'exponential'` | `'hinge'` | `'logit'` | `'quadratic'` | указатель на функцию

Функция потерь, заданная как разделенная разделенными запятой парами, состоящая из 'LossFun' и встроенное имя функции потери или указатель на функцию.

В следующей таблице перечислены доступные функции потерь. Задайте один с помощью соответствующего вектора символов или строкового скаляра.

Значение	Описание
`'binodeviance'`	Биномиальное отклонение
`'classiferror'`	Неверно классифицированный коэффициент в десятичных числах
`'exponential'`	Экспоненциальные потери
`'hinge'`	Потеря шарнира
`'logit'`	Логистические потери
`'mincost'`	Минимальные ожидаемые затраты на неправильную классификацию (для классификационных оценок, которые являются апостериорными вероятностями)
`'quadratic'`	Квадратичные потери

'mincost' подходит для классификационных оценок, которые являются апостериорными вероятностями. Модели дискриминантного анализа возвращают апостериорные вероятности классификационных оценок как по умолчанию (см predict).

Задайте свою собственную функцию, используя обозначение указателя на функцию.
Предположим, что n количество наблюдений в X и K быть количеством различных классов (numel(obj.ClassNames)). Ваша функция должна иметь эту подпись
```
lossvalue = lossfun(C,S,W,Cost)
```
где:
- Выходной аргумент lossvalue является скаляром.
- Вы выбираете имя функции (lossfun).
- C является n-by- K логическая матрица со строками, указывающими, какому классу принадлежит соответствующее наблюдение. Порядок столбцов соответствует порядку классов в obj.ClassNames.
  Конструкция C путем установки C(p,q) = 1 если наблюдение p находится в q классов, для каждой строки. Установите все другие элементы строки p на 0.
- S является n-by- K числовая матрица классификационных оценок. Порядок столбцов соответствует порядку классов в obj.ClassNames. S является матрицей классификационных оценок, подобной выходным данным predict.
- W является n-by-1 числовой вектор весов наблюдений. Если вы сдаете Wпрограммное обеспечение нормирует их в сумме к 1.
- Cost является K -by- K числовая матрица затрат на неправильную классификацию. Для примера, Cost = ones(K) - eye(K) задает стоимость 0 для правильной классификации и 1 для неправильной классификации.
Задайте свою функцию, используя 'LossFun', @ lossfun.

Для получения дополнительной информации о функциях потерь смотрите Классификационные потери.

Типы данных: char | string | function_handle

Выходные аргументы

`L`	Классификационная ошибка, скаляр. Смысл ошибки зависит от значений в `weights` и `lossfun`. См. Классификационные потери.

Примеры

Вычислите повторно замещенную ошибку классификации для данных радужной оболочки глаза Фишера:

load fisheriris
obj = fitcdiscr(meas,species);
L = resubLoss(obj)

L =
    0.0200

Подробнее о

расширить все

Классификационные потери

Classification loss функции измеряют прогнозирующую неточность классификационных моделей. Когда вы сравниваете один и тот же тип потерь среди многих моделей, более низкая потеря указывает на лучшую прогнозирующую модель.

Рассмотрим следующий сценарий.

L - средневзвешенные классификационные потери.
n - размер выборки.
Для двоичной классификации:
- _yj - наблюдаемая метка класса. Программное обеспечение кодирует его как -1 или 1, указывая на отрицательный или положительный класс (или первый или второй класс в ClassNames свойство), соответственно.
- f (_Xj) является баллом классификации положительного класса для j наблюдений (строка) X данных предиктора.
- _mj = _yj f ₍Xj) является классификационной оценкой для классификации j наблюдений в класс, относящийся к yj. Положительные значения mj указывают на правильную классификацию и не вносят большой вклад в средние потери. Отрицательные значения mj указывают на неправильную классификацию и вносят значительный вклад в среднюю потерю.
Для алгоритмов, которые поддерживают многоклассовую классификацию (то есть K ≥ 3):
- _yj^* - вектор с K - 1 нулями, с 1 в положении, соответствующем истинному, наблюдаемому классу _yj. Для примера, если истинный класс второго наблюдения является третьим классом и K = 4, то y 2^* = [0 0 1 0]′. Порядок классов соответствует порядку в ClassNames свойство модели входа.
- f (_Xj) является вектором K длины счетов классов для j наблюдений X данных предиктора. Порядок счетов соответствует порядку классов в ClassNames свойство модели входа.
- _mj = _yj^*′ f _{(<reservedrangesplaceholder1>)}. Поэтому mj является скалярной классификационной оценкой, которую модель предсказывает для истинного наблюдаемого класса.
Вес для j наблюдения _wj. Программа нормализует веса наблюдений так, чтобы они суммировались с соответствующей вероятностью предыдущего класса. Программное обеспечение также нормализует предыдущие вероятности, поэтому они равны 1. Поэтому,

$\sum_{j = 1}^{n} w_{j} = 1.$

С учетом этого сценария в следующей таблице описываются поддерживаемые функции потерь, которые можно задать при помощи 'LossFun' аргумент пары "имя-значение".

Функция потерь	Значение `LossFun`	Уравнение
Биномиальное отклонение	`'binodeviance'`	$L = \sum_{j = 1}^{n} w_{j} \log {1 + \exp [- 2 m_{j}]} .$
Неверно классифицированный коэффициент в десятичных числах	`'classiferror'`	$L = \sum_{j = 1}^{n} w_{j} I {{\hat{y}}_{j} \neq y_{j}} .$ ${\hat{y}}_{j}$ - метка класса, соответствующая классу с максимальным счетом. I {·} является функцией индикации.
Потери перекрестной энтропии	`'crossentropy'`	`'crossentropy'` подходит только для моделей нейронных сетей. Взвешенные потери перекрестной энтропии $L = - \sum_{j = 1}^{n} \frac{{\tilde{w}}_{j} \log (m_{j})}{K n},$ где веса ${\tilde{w}}_{j}$ нормированы в сумме к n вместо 1.
Экспоненциальные потери	`'exponential'`	$L = \sum_{j = 1}^{n} w_{j} \exp (- m_{j}) .$
Потеря шарнира	`'hinge'`	$L = \sum_{j = 1}^{n} w_{j} \max {0, 1 - m_{j}} .$
Логит потеря	`'logit'`	$L = \sum_{j = 1}^{n} w_{j} \log (1 + \exp (- m_{j})) .$
Минимальные ожидаемые затраты на неправильную классификацию	`'mincost'`	`'mincost'` подходит только, если классификационные оценки апостериорные вероятности. Программа вычисляет взвешенные минимальные ожидаемые затраты классификации, используя эту процедуру для наблюдений j = 1,..., n. Оцените ожидаемые затраты на неправильную классификацию классификации _Xj наблюдений в k классов: $γ_{j k} = {(f {(X_{j})}^{'} C)}_{k} .$ f (_Xj) является вектором-столбцом апостериорных вероятностей классов для двоичной и многоклассовой классификации для _Xj наблюдений. C - матрица затрат, сохраненная в `Cost` свойство модели. Для j наблюдения спрогнозируйте метку класса, соответствующую минимальной ожидаемой стоимости неправильной классификации: ${\hat{y}}_{j} = \underset{k = 1, ..., K}{argmin} γ_{j k} .$ Используя C, идентифицируйте понесенные затраты (_cj) для создания предсказания. Взвешенное среднее значение минимальных ожидаемых потерь от неправильной классификации $L = \sum_{j = 1}^{n} w_{j} c_{j} .$ Если вы используете матрицу затрат по умолчанию (значение элемента которой 0 для правильной классификации и 1 для неправильной классификации), то `'mincost'` потеря эквивалентна `'classiferror'` потеря.
Квадратичные потери	`'quadratic'`	$L = \sum_{j = 1}^{n} w_{j} {(1 - m_{j})}^{2} .$

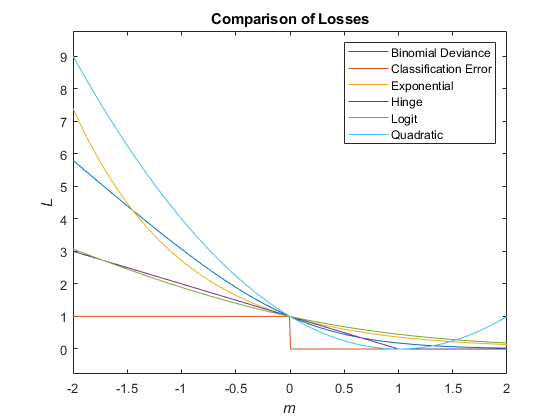
Этот рисунок сравнивает функции потерь (кроме 'crossentropy' и 'mincost') по счету m для одного наблюдения. Некоторые функции нормированы, чтобы пройти через точку (0,1).

Апостериорная вероятность

Апостериорная вероятность того, что x точек принадлежит классу k, является продуктом априорной вероятности и многомерной нормальной плотности. Плотность распределения многомерного нормального с 1-by-<reservedrangesplaceholder6>, средним μk и d d ковариацией Σ <reservedrangesplaceholder2> в точке 1-by-<reservedrangesplaceholder1> x,

$P (x | k) = \frac{1}{{({(2 π)}^{d} | Σ_{k} |)}^{1 / 2}} \exp (- \frac{1}{2} (x - μ_{k}) Σ_{k}^{- 1} {(x - μ_{k})}^{T}),$

где $| Σ_{k} |$ является определяющим, и, k, $Σ_{k}^{- 1}$ - обратная матрица.

Пусть P (k) представляет априорную вероятность k класса. Тогда апостериорная вероятность того, что x наблюдения имеет класс k,

$\hat{P} (k | x) = \frac{P (x | k) P (k)}{P (x)},$

где P (<reservedrangesplaceholder6>) является постоянной нормализацией, сумма по k P (x | k) P (<reservedrangesplaceholder0>).

Предварительная вероятность

Предыдущая вероятность является одним из трех вариантов:

'uniform' - априорная вероятность k классов на единицу превышает общее количество классов.
'empirical' - априорная вероятность k классов количество обучающих выборок класса k разделенный на общее количество обучающих выборок.
Custom - априорная вероятность k классов является kпервый элемент prior вектор. Посмотрите fitcdiscr.

После создания классификационной модели (Mdl) можно задать предшествующее с помощью записи через точку:

Mdl.Prior = v;

где v является вектором положительных элементов, представляющих частоту, с которой происходит каждый элемент. Вам не нужно переобучать классификатор, когда вы задаете новый предыдущий.

Стоимость

Матрица ожидаемых затрат на наблюдение определяется в Затратах.

См. также

ClassificationDiscriminant | fitcdiscr | loss

Темы

Классификация дискриминантного анализа

Документация

resubLoss

Синтаксис

Описание

Входные параметры

Аргументы в виде пар имя-значение

`'LossFun'` - Функция потерь
`'mincost'` (по умолчанию) | `'binodeviance'` | `'classiferror'` | `'exponential'` | `'hinge'` | `'logit'` | `'quadratic'` | указатель на функцию

Выходные аргументы

Примеры

Подробнее о

Классификационные потери

Апостериорная вероятность

Предварительная вероятность

Стоимость

См. также

Темы

Statistics and Machine Learning Toolbox документация

Поддержка

Документация

resubLoss

Синтаксис

Описание

Входные параметры

Аргументы в виде пар имя-значение

'LossFun' - Функция потерь 'mincost' (по умолчанию) | 'binodeviance' | 'classiferror' | 'exponential' | 'hinge' | 'logit' | 'quadratic' | указатель на функцию

Выходные аргументы

Примеры

Подробнее о

Классификационные потери

Апостериорная вероятность

Предварительная вероятность

Стоимость

См. также

Темы

Statistics and Machine Learning Toolbox документация

Поддержка

`'LossFun'` - Функция потерь
`'mincost'` (по умолчанию) | `'binodeviance'` | `'classiferror'` | `'exponential'` | `'hinge'` | `'logit'` | `'quadratic'` | указатель на функцию