loss

Ошибка классификации

Синтаксис

L = loss(tree,TBL,ResponseVarName)

L = loss(tree,TBL,Y)

L = loss(tree,X,Y)

L = loss(___,Name,Value)

[L,se,NLeaf,bestlevel]
= loss(___)

Описание

L = loss(tree,TBL,ResponseVarName) возвращает скаляр, представляющий, насколько хорошо tree классифицирует данные в TBL, когда TBL.ResponseVarName содержит истинные классификации.

При расчете потерь loss нормализует вероятности классов в Y к вероятностям класса, используемым для обучения, хранящимся в Prior свойство tree.

L = loss(tree,TBL,Y) возвращает скаляр, представляющий, насколько хорошо tree классифицирует данные в TBL, когда Y содержит истинные классификации.

L = loss(tree,X,Y) возвращает скаляр, представляющий, насколько хорошо tree классифицирует данные в X, когда Y содержит истинные классификации.

L = loss(___,Name,Value) возвращает потерю с дополнительными опциями, заданными одним или несколькими Name,Value аргументы в виде пар, с использованием любого из предыдущих синтаксисов. Для примера можно задать функцию потерь или веса наблюдений.

[L,se,NLeaf,bestlevel] = loss(___) также возвращает вектор стандартных ошибок ошибок классификации (se), вектор чисел листовых узлов в деревьях последовательности обрезки (NLeaf) и лучший уровень обрезки, как определено в TreeSize Пара "имя-значение" (bestlevel).

Входные параметры

расширить все

`tree` - Обученное дерево классификации
`ClassificationTree` объект модели | `CompactClassificationTree` объект модели

Обученное дерево классификации, заданное как ClassificationTree или CompactClassificationTree объект модели. То есть tree является обученной классификационной моделью, возвращенной fitctree или compact.

`TBL` - Выборочные данные
таблица

Выборочные данные, заданный как таблица. Каждая строка TBL соответствует одному наблюдению, и каждый столбец соответствует одной переменной предиктора. Опционально TBL может содержать дополнительные столбцы для переменной отклика и весов наблюдений. TBL должны содержать все предикторы, используемые для обучения tree. Многополюсные переменные и массивы ячеек, отличные от массивов ячеек векторов символов, не разрешены.

Если TBL содержит переменную отклика, используемую для обучения tree, тогда вам не нужно указывать ResponseVarName или Y.

Если вы обучаете tree использование выборочных данных, содержащихся в table, тогда входные данные для этого метода также должны быть в таблице.

Типы данных: table

`X` - Данные для классификации
числовая матрица

Данные для классификации, заданные как числовая матрица. Каждая строка X представляет одно наблюдение, и каждый столбец представляет один предиктор. X должны иметь одинаковое число столбцов в качестве данных, используемых для обучения tree. X должно иметь одинаковое число строк как количество элементов в Y.

Типы данных: single | double

`ResponseVarName` - Имя переменной отклика
имя переменной в `TBL`

Имя переменной отклика, заданное как имя переменной в TBL. Если TBL содержит переменную отклика, используемую для обучения tree, тогда вам не нужно указывать ResponseVarName.

Если вы задаете ResponseVarName, тогда вы должны сделать это как вектор символов или строковый скаляр. Для примера, если переменная отклика сохранена как TBL.Response, затем укажите его следующим 'Response'. В противном случае программное обеспечение обрабатывает все столбцы TBL, включая TBL.ResponseVarName, как предикторы.

Переменная отклика должна быть категориальными символьными или строковыми массивами, логическим или числовым вектором или массивом ячеек из векторов символов. Если переменная отклика является символьным массивом, то каждый элемент должен соответствовать одной строке массива.

Типы данных: char | string

`Y` - Метки классов
категориальный массив | символьный массив | строковые массивы | логический вектор | числовой вектор | массив ячеек из векторов символов

Метки класса, заданные как категориальные символьные или строковые массивы, логический или числовой вектор или массив ячеек из векторов символов. Y должен быть того же типа, что и классификация, используемая для обучения tree, и его количество элементов должно равняться количеству строк X.

Аргументы в виде пар имя-значение

Задайте необязательные разделенные разделенными запятой парами Name,Value аргументы. Name - имя аргумента и Value - соответствующее значение. Name должны находиться внутри кавычек. Можно задать несколько аргументов в виде пар имен и значений в любом порядке Name1,Value1,...,NameN,ValueN.

`'LossFun'` - Функция потерь
`'mincost'` (по умолчанию) | `'binodeviance'` | `'classiferror'` | `'exponential'` | `'hinge'` | `'logit'` | `'quadratic'` | указатель на функцию

Функция потерь, заданная как разделенная разделенными запятой парами, состоящая из 'LossFun' и встроенное имя функции потери или указатель на функцию.

В следующей таблице перечислены доступные функции потерь. Задайте один с помощью соответствующего вектора символов или строкового скаляра.

Значение	Описание
`'binodeviance'`	Биномиальное отклонение
`'classiferror'`	Неверно классифицированный коэффициент в десятичных числах
`'exponential'`	Экспоненциальные потери
`'hinge'`	Потеря шарнира
`'logit'`	Логистические потери
`'mincost'`	Минимальные ожидаемые затраты на неправильную классификацию (для классификационных оценок, которые являются апостериорными вероятностями)
`'quadratic'`	Квадратичные потери

'mincost' подходит для классификационных оценок, которые являются апостериорными вероятностями. Деревья классификации возвращают апостериорные вероятности классификационных оценок как по умолчанию (см predict).

Задайте свою собственную функцию, используя обозначение указателя на функцию.
Предположим, что n количество наблюдений в X и K быть количеством различных классов (numel(tree.ClassNames)). Ваша функция должна иметь эту подпись
```
lossvalue = lossfun(C,S,W,Cost)
```
где:
- Выходной аргумент lossvalue является скаляром.
- Вы выбираете имя функции (lossfun).
- C является n-by- K логическая матрица со строками, указывающими, какому классу принадлежит соответствующее наблюдение. Порядок столбцов соответствует порядку классов в tree.ClassNames.
  Конструкция C путем установки C(p,q) = 1 если наблюдение p находится в q классов, для каждой строки. Установите все другие элементы строки p на 0.
- S является n-by- K числовая матрица классификационных оценок. Порядок столбцов соответствует порядку классов в tree.ClassNames. S является матрицей классификационных оценок, подобной выходным данным predict.
- W является n-by-1 числовой вектор весов наблюдений. Если вы сдаете Wпрограммное обеспечение нормирует их в сумме к 1.
- Cost является K -by- K числовая матрица затрат на неправильную классификацию. Для примера, Cost = ones(K) - eye(K) задает стоимость 0 для правильной классификации и 1 для неправильной классификации.
Задайте свою функцию, используя 'LossFun', @ lossfun.

Для получения дополнительной информации о функциях потерь смотрите Классификационные потери.

Типы данных: char | string | function_handle

`'Weights'` - Веса наблюдений
`ones(size(X,1),1)` (по умолчанию) | имя переменной в `TBL` | числовой вектор положительных значений

Веса наблюдений, заданные как разделенная разделенными запятой парами, состоящая из 'Weights' и числовой вектор положительных значений или имя переменной в TBL.

Если вы задаете Weights в виде числового вектора, затем размера Weights должно быть равно количеству строк в X или TBL.

Если вы задаете Weights как имя переменной в TBL, вы должны сделать это как вектор символов или строковый скаляр. Для примера, если веса сохранены как TBL.W, затем укажите его следующим 'W'. В противном случае программное обеспечение обрабатывает все столбцы TBL, включая TBL.W, как предикторы.

loss нормализует веса так, чтобы веса наблюдений в каждой сумме классов соответствовали предшествующей вероятности этого класса. Когда вы поставляете Weights, loss вычисляет взвешенные классификационные потери.

Типы данных: single | double | char | string

Name,Value аргументы, связанные с обрезкой поддеревьев:

`'Subtrees'` - Уровень обрезки
0 (по умолчанию) | вектор неотрицательных целых чисел | `'all'`

Уровень обрезки, заданный как разделенная разделенными запятой парами, состоящая из 'Subtrees' и вектор неотрицательных целых чисел в порядке возрастания или 'all'.

Если вы задаете вектор, то все элементы должны быть как минимум 0 и самое большее max(tree.PruneList). 0 указывает полное, несрезанное дерево и max(tree.PruneList) указывает полностью обрезанное дерево (т.е. только корневой узел).

Если вы задаете 'all', затем loss работает со всеми поддеревьями (т.е. со всей последовательностью обрезки). Эта спецификация эквивалентна использованию 0:max(tree.PruneList).

loss черносливы tree каждому уровню, указанному в Subtrees, а затем оценивает соответствующие выходные аргументы. Размер Subtrees определяет размер некоторых выходных аргументов.

Для вызова Subtrees, свойства PruneList и PruneAlpha от tree должно быть непустым. Другими словами, расти tree путем установки 'Prune','on', или путем обрезки tree использование prune.

Пример: 'Subtrees','all'

Типы данных: single | double | char | string

`'TreeSize'` - Размер дерева
`'se'` (по умолчанию) | `'min'`

Размер дерева, заданный как разделенная разделенными запятой парами, состоящая из 'TreeSize' и одно из следующих значений:

'se' — loss возвращает наивысший уровень обрезки с потерями в пределах одного стандартного отклонения от минимального (L+ se, где L и se относятся к наименьшему значению в Subtrees).
'min' — loss возвращает элемент Subtrees с наименьшими потерями, обычно наименьший элемент Subtrees.

Выходные аргументы

расширить все

`L` - Классификационные потери
вектор скалярных значений

Классификационные потери, возвращенные в качестве вектора длину Subtrees. Смысл ошибки зависит от значений в Weights и LossFun.

`se` - Стандартная ошибка потерь
вектор скалярных значений

Стандартная ошибка потерь, возвращенная в качестве вектора длина Subtrees.

`NLeaf` - Количество листовых узлов
вектор целочисленных значений

Количество листьев (терминальных узлов) в обрезанных поддеревьях, возвращаемое как вектор длину Subtrees.

`bestlevel` - Лучший уровень обрезки
скалярное значение

Лучший уровень обрезки, как определено в TreeSize Пара "имя-значение", возвращенный как скаляр, значение которого зависит от TreeSize:

TreeSize = 'se' — loss возвращает наивысший уровень обрезки с потерями в пределах одного стандартного отклонения от минимального (L+ se, где L и se относятся к наименьшему значению в Subtrees).
TreeSize = 'min' — loss возвращает элемент Subtrees с наименьшими потерями, обычно наименьший элемент Subtrees.

По умолчанию bestlevel - уровень обрезки, который дает потерю в пределах одного стандартного отклонения минимальных потерь.

Примеры

расширить все

Вычислите ошибку классификации в выборке

Открыть Live Script

Вычислите повторно замещенную ошибку классификации для ionosphere набор данных.

load ionosphere
tree = fitctree(X,Y);
L = loss(tree,X,Y)

L = 0.0114

Исследуйте классификационную ошибку для каждого поддерева

Открыть Live Script

Необрезанные деревья решений, как правило, перегружаются. Один из способов сбалансировать сложность модели и эффективности вне выборки - это обрезать дерево (или ограничить его рост), чтобы эффективность в выборке и вне выборки были удовлетворительными.

Загрузите набор данных радужки Фишера. Разделите данные на наборы для обучения (50%) и валидации (50%).

load fisheriris
n = size(meas,1);
rng(1) % For reproducibility
idxTrn = false(n,1);
idxTrn(randsample(n,round(0.5*n))) = true; % Training set logical indices 
idxVal = idxTrn == false;                  % Validation set logical indices

Создайте дерево классификации с помощью набора обучающих данных.

Mdl = fitctree(meas(idxTrn,:),species(idxTrn));

Просмотрите дерево классификации.

view(Mdl,'Mode','graph');

Figure Classification tree viewer contains an axes and other objects of type uimenu, uicontrol. The axes contains 18 objects of type line, text.

Классификационное дерево имеет четыре уровня обрезки. Уровень 0 является полным, несрезанным деревом (как показано). Уровень 3 является только корневым узлом (то есть без разделений).

Исследуйте ошибку классификации обучающей выборки для каждого поддерева (или уровня обрезки), исключая самый высокий уровень.

m = max(Mdl.PruneList) - 1;
trnLoss = resubLoss(Mdl,'SubTrees',0:m)

trnLoss = 3×1

    0.0267
    0.0533
    0.3067

Полное, несрезанное дерево ошибочно классифицирует около 2,7% обучающих наблюдений.
Дерево, обрезанное до уровня 1, неправильно классифицирует около 5,3% обучающих наблюдений.
Дерево, обрезанное до уровня 2 (то есть пень), неправильно классифицирует около 30,6% обучающих наблюдений.

Исследуйте ошибку классификации выборок валидации на каждом уровне, исключая самый высокий уровень.

valLoss = loss(Mdl,meas(idxVal,:),species(idxVal),'SubTrees',0:m)

valLoss = 3×1

    0.0369
    0.0237
    0.3067

Полное, несрезанное дерево ошибочно классифицирует около 3,7% наблюдений валидации.
Дерево, обрезанное до уровня 1, неправильно классифицирует около 2,4% наблюдений валидации.
Дерево, обрезанное до уровня 2 (то есть пень), неправильно классифицирует около 30,7% наблюдений валидации.

Чтобы сбалансировать сложность модели и несовпадающую эффективность, рассмотрите обрезку Mdl на уровень 1.

pruneMdl = prune(Mdl,'Level',1);
view(pruneMdl,'Mode','graph')

Figure Classification tree viewer contains an axes and other objects of type uimenu, uicontrol. The axes contains 12 objects of type line, text.

Подробнее о

расширить все

Классификационные потери

Classification loss функции измеряют прогнозирующую неточность классификационных моделей. Когда вы сравниваете один и тот же тип потерь среди многих моделей, более низкая потеря указывает на лучшую прогнозирующую модель.

Рассмотрим следующий сценарий.

L - средневзвешенные классификационные потери.
n - размер выборки.
Для двоичной классификации:
- _yj - наблюдаемая метка класса. Программное обеспечение кодирует его как -1 или 1, указывая на отрицательный или положительный класс (или первый или второй класс в ClassNames свойство), соответственно.
- f (_Xj) является баллом классификации положительного класса для j наблюдений (строка) X данных предиктора.
- _mj = _yj f ₍Xj) является классификационной оценкой для классификации j наблюдений в класс, относящийся к yj. Положительные значения mj указывают на правильную классификацию и не вносят большой вклад в средние потери. Отрицательные значения mj указывают на неправильную классификацию и вносят значительный вклад в среднюю потерю.
Для алгоритмов, которые поддерживают многоклассовую классификацию (то есть K ≥ 3):
- _yj^* - вектор с K - 1 нулями, с 1 в положении, соответствующем истинному, наблюдаемому классу _yj. Для примера, если истинный класс второго наблюдения является третьим классом и K = 4, то y 2^* = [0 0 1 0]′. Порядок классов соответствует порядку в ClassNames свойство модели входа.
- f (_Xj) является вектором K длины счетов классов для j наблюдений X данных предиктора. Порядок счетов соответствует порядку классов в ClassNames свойство модели входа.
- _mj = _yj^*′ f _{(<reservedrangesplaceholder1>)}. Поэтому mj является скалярной классификационной оценкой, которую модель предсказывает для истинного наблюдаемого класса.
Вес для j наблюдения _wj. Программа нормализует веса наблюдений так, чтобы они суммировались с соответствующей вероятностью предыдущего класса. Программное обеспечение также нормализует предыдущие вероятности, поэтому они равны 1. Поэтому,

$\sum_{j = 1}^{n} w_{j} = 1.$

С учетом этого сценария в следующей таблице описываются поддерживаемые функции потерь, которые можно задать при помощи 'LossFun' аргумент пары "имя-значение".

Функция потерь	Значение `LossFun`	Уравнение
Биномиальное отклонение	`'binodeviance'`	$L = \sum_{j = 1}^{n} w_{j} \log {1 + \exp [- 2 m_{j}]} .$
Неверно классифицированный коэффициент в десятичных числах	`'classiferror'`	$L = \sum_{j = 1}^{n} w_{j} I {{\hat{y}}_{j} \neq y_{j}} .$ ${\hat{y}}_{j}$ - метка класса, соответствующая классу с максимальным счетом. I {·} является функцией индикации.
Потери перекрестной энтропии	`'crossentropy'`	`'crossentropy'` подходит только для моделей нейронных сетей. Взвешенные потери перекрестной энтропии $L = - \sum_{j = 1}^{n} \frac{{\tilde{w}}_{j} \log (m_{j})}{K n},$ где веса ${\tilde{w}}_{j}$ нормированы в сумме к n вместо 1.
Экспоненциальные потери	`'exponential'`	$L = \sum_{j = 1}^{n} w_{j} \exp (- m_{j}) .$
Потеря шарнира	`'hinge'`	$L = \sum_{j = 1}^{n} w_{j} \max {0, 1 - m_{j}} .$
Логит потеря	`'logit'`	$L = \sum_{j = 1}^{n} w_{j} \log (1 + \exp (- m_{j})) .$
Минимальные ожидаемые затраты на неправильную классификацию	`'mincost'`	`'mincost'` подходит только, если классификационные оценки апостериорные вероятности. Программа вычисляет взвешенные минимальные ожидаемые затраты классификации, используя эту процедуру для наблюдений j = 1,..., n. Оцените ожидаемые затраты на неправильную классификацию классификации _Xj наблюдений в k классов: $γ_{j k} = {(f {(X_{j})}^{'} C)}_{k} .$ f (_Xj) является вектором-столбцом апостериорных вероятностей классов для двоичной и многоклассовой классификации для _Xj наблюдений. C - матрица затрат, сохраненная в `Cost` свойство модели. Для j наблюдения спрогнозируйте метку класса, соответствующую минимальной ожидаемой стоимости неправильной классификации: ${\hat{y}}_{j} = \underset{k = 1, ..., K}{argmin} γ_{j k} .$ Используя C, идентифицируйте понесенные затраты (_cj) для создания предсказания. Взвешенное среднее значение минимальных ожидаемых потерь от неправильной классификации $L = \sum_{j = 1}^{n} w_{j} c_{j} .$ Если вы используете матрицу затрат по умолчанию (значение элемента которой 0 для правильной классификации и 1 для неправильной классификации), то `'mincost'` потеря эквивалентна `'classiferror'` потеря.
Квадратичные потери	`'quadratic'`	$L = \sum_{j = 1}^{n} w_{j} {(1 - m_{j})}^{2} .$

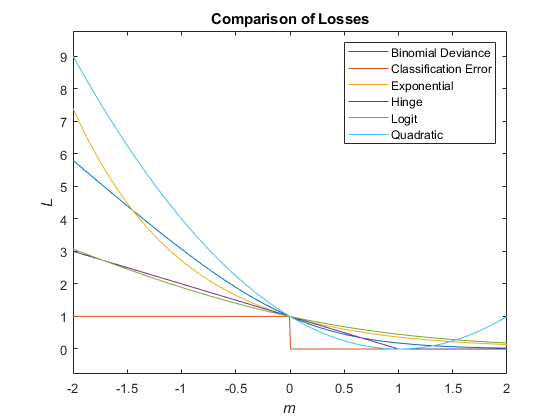
Этот рисунок сравнивает функции потерь (кроме 'crossentropy' и 'mincost') по счету m для одного наблюдения. Некоторые функции нормированы, чтобы пройти через точку (0,1).

Истинные затраты на неправильную классификацию

Истинная стоимость неправильной классификации является стоимостью классификации наблюдения в неправильный класс.

Можно задать истинные затраты на неправильную классификацию по классам с помощью 'Cost' аргумент имя-значение при создании классификатора. Cost(i,j) - стоимость классификации наблюдений в классы j когда его истинный класс i. По умолчанию Cost(i,j)=1 если i~=j, и Cost(i,j)=0 если i=j. Другими словами, стоимость 0 для правильной классификации и 1 для неправильной классификации.

Ожидаемые затраты на неправильную классификацию

Ожидаемая стоимость неправильной классификации за наблюдение является усредненной стоимостью классификации наблюдений по каждому классу.

Предположим, у вас есть Nobs наблюдения, которые вы хотите классифицировать с помощью обученного классификатора, и у вас есть K классы. Наблюдения помещаются в матрицу X с одним наблюдением за строкой.

Матрица ожидаемых затрат CE имеет размер Nobs-by- K. Каждая строка CE содержит ожидаемые (средние) затраты на классификацию наблюдений по каждому из K классы. CE(n,k) является

$\sum_{i = 1}^{K} \hat{P} (i | X (n)) C (k | i),$

где:

K - количество классов.
$\hat{P} (i | X (n))$ - апостериорная вероятность i классов для X наблюдений (n).
$C (k | i)$ - истинная стоимость неправильной классификации при классификации наблюдения как k, когда его истинный класс i.

Счет (дерево)

Для деревьев score классификации узла листа является апостериорной вероятностью классификации в этом узле. Апостериорная вероятность классификации в узле - это количество обучающих последовательностей, которые ведут к этому узлу с классификацией, разделенной на количество обучающих последовательностей, которые ведут к этому узлу.

Например, рассмотрите классификацию предиктора X как true когда X < 0.15 или X > 0.95, и X в противном случае ложь.

Сгенерируйте 100 случайных точек и классифицируйте их:

rng(0,'twister') % for reproducibility
X = rand(100,1);
Y = (abs(X - .55) > .4);
tree = fitctree(X,Y);
view(tree,'Mode','Graph')

Обрезать дерево:

tree1 = prune(tree,'Level',1);
view(tree1,'Mode','Graph')

Обрезанное дерево правильно классифицирует наблюдения, которые меньше 0,15, как true. Он также правильно классифицирует наблюдения от .15 до .94 как false. Однако он неправильно классифицирует наблюдения, которые больше 94, как false. Поэтому счет для наблюдений, которые больше 15, должны быть около .05/.85 = .06 для trueи примерно .8/.85 = .94 для false.

Вычислите счета предсказания для первых 10 строк X:

[~,score] = predict(tree1,X(1:10));
[score X(1:10,:)]

ans = 10×3

    0.9059    0.0941    0.8147
    0.9059    0.0941    0.9058
         0    1.0000    0.1270
    0.9059    0.0941    0.9134
    0.9059    0.0941    0.6324
         0    1.0000    0.0975
    0.9059    0.0941    0.2785
    0.9059    0.0941    0.5469
    0.9059    0.0941    0.9575
    0.9059    0.0941    0.9649

Действительно, каждое значение X (самый правый столбец), который меньше 0,15 имеет связанные счета (левый и центральный столбцы) 0 и 1, в то время как другие значения X имеют сопоставленные счета 0.91 и 0.09. The различия (счет 0.09 вместо ожидаемого .06) обусловлено статистическим колебанием: существуют 8 наблюдения в X в области значений (.95,1) вместо ожидаемого 5 наблюдения.

Расширенные возможности

Длинные» массивы
Осуществление вычислений с массивами, которые содержат больше строк, чем помещается в памяти.

Указания и ограничения по применению:

Поддерживается только один выход.
Вы можете использовать модели, обученные на памяти или высоких данных с этой функцией.

Для получения дополнительной информации см. Раздел «Длинные массивы»

См. также

edge | fitctree | margin | predict

Документация

loss

Синтаксис

Описание

Входные параметры

`tree` - Обученное дерево классификации
`ClassificationTree` объект модели | `CompactClassificationTree` объект модели

`TBL` - Выборочные данные
таблица

`X` - Данные для классификации
числовая матрица

`ResponseVarName` - Имя переменной отклика
имя переменной в `TBL`

`Y` - Метки классов
категориальный массив | символьный массив | строковые массивы | логический вектор | числовой вектор | массив ячеек из векторов символов

Аргументы в виде пар имя-значение

`'LossFun'` - Функция потерь
`'mincost'` (по умолчанию) | `'binodeviance'` | `'classiferror'` | `'exponential'` | `'hinge'` | `'logit'` | `'quadratic'` | указатель на функцию

`'Weights'` - Веса наблюдений
`ones(size(X,1),1)` (по умолчанию) | имя переменной в `TBL` | числовой вектор положительных значений

`'Subtrees'` - Уровень обрезки
0 (по умолчанию) | вектор неотрицательных целых чисел | `'all'`

`'TreeSize'` - Размер дерева
`'se'` (по умолчанию) | `'min'`

Выходные аргументы

`L` - Классификационные потери
вектор скалярных значений

`se` - Стандартная ошибка потерь
вектор скалярных значений

`NLeaf` - Количество листовых узлов
вектор целочисленных значений

`bestlevel` - Лучший уровень обрезки
скалярное значение

Примеры

Вычислите ошибку классификации в выборке

Исследуйте классификационную ошибку для каждого поддерева

Подробнее о

Классификационные потери

Истинные затраты на неправильную классификацию

Ожидаемые затраты на неправильную классификацию

Счет (дерево)

Расширенные возможности

Длинные» массивы
Осуществление вычислений с массивами, которые содержат больше строк, чем помещается в памяти.

См. также

Statistics and Machine Learning Toolbox документация

Поддержка

Документация

loss

Синтаксис

Описание

Входные параметры

tree - Обученное дерево классификации ClassificationTree объект модели | CompactClassificationTree объект модели

TBL - Выборочные данные таблица

X - Данные для классификации числовая матрица

ResponseVarName - Имя переменной отклика имя переменной в TBL

Y - Метки классов категориальный массив | символьный массив | строковые массивы | логический вектор | числовой вектор | массив ячеек из векторов символов

Аргументы в виде пар имя-значение

'LossFun' - Функция потерь 'mincost' (по умолчанию) | 'binodeviance' | 'classiferror' | 'exponential' | 'hinge' | 'logit' | 'quadratic' | указатель на функцию

'Weights' - Веса наблюдений ones(size(X,1),1) (по умолчанию) | имя переменной в TBL | числовой вектор положительных значений

'Subtrees' - Уровень обрезки 0 (по умолчанию) | вектор неотрицательных целых чисел | 'all'

'TreeSize' - Размер дерева 'se' (по умолчанию) | 'min'

Выходные аргументы

L - Классификационные потери вектор скалярных значений

se - Стандартная ошибка потерь вектор скалярных значений

NLeaf - Количество листовых узлов вектор целочисленных значений

bestlevel - Лучший уровень обрезки скалярное значение

Примеры

Вычислите ошибку классификации в выборке

Исследуйте классификационную ошибку для каждого поддерева

Подробнее о

Классификационные потери

Истинные затраты на неправильную классификацию

Ожидаемые затраты на неправильную классификацию

Счет (дерево)

Расширенные возможности

Длинные» массивы Осуществление вычислений с массивами, которые содержат больше строк, чем помещается в памяти.

См. также

Statistics and Machine Learning Toolbox документация

Поддержка

`tree` - Обученное дерево классификации
`ClassificationTree` объект модели | `CompactClassificationTree` объект модели

`TBL` - Выборочные данные
таблица

`X` - Данные для классификации
числовая матрица

`ResponseVarName` - Имя переменной отклика
имя переменной в `TBL`

`Y` - Метки классов
категориальный массив | символьный массив | строковые массивы | логический вектор | числовой вектор | массив ячеек из векторов символов

`'LossFun'` - Функция потерь
`'mincost'` (по умолчанию) | `'binodeviance'` | `'classiferror'` | `'exponential'` | `'hinge'` | `'logit'` | `'quadratic'` | указатель на функцию

`'Weights'` - Веса наблюдений
`ones(size(X,1),1)` (по умолчанию) | имя переменной в `TBL` | числовой вектор положительных значений

`'Subtrees'` - Уровень обрезки
0 (по умолчанию) | вектор неотрицательных целых чисел | `'all'`

`'TreeSize'` - Размер дерева
`'se'` (по умолчанию) | `'min'`

`L` - Классификационные потери
вектор скалярных значений

`se` - Стандартная ошибка потерь
вектор скалярных значений

`NLeaf` - Количество листовых узлов
вектор целочисленных значений

`bestlevel` - Лучший уровень обрезки
скалярное значение

Длинные» массивы
Осуществление вычислений с массивами, которые содержат больше строк, чем помещается в памяти.