Quasi-random number generators (QRNGs) производят высоко равномерные выборки единичного гиперкуба. QRNG минимизируют discrepancy между распределением сгенерированных точек и распределением с равными пропорциями точек в каждом подкубе равномерного разбиения гиперкуба. В результате QRNG систематически заполняют «отверстия» в любом начальном сегменте сгенерированной квазислучайной последовательности.
В отличие от псевдослучайных последовательностей, описанных в Common Pseudorandom Number Generation Methods, квазислучайные последовательности проваливают многие статистические тесты на случайность. Аппроксимация истинной случайности, однако, не является их целью. Квазислучайные последовательности стремятся заполнить пространство равномерно и сделать это таким образом, чтобы начальные сегменты аппроксимировали это поведение до заданной плотности.
Приложения QRNG включают:
Квази-Монте-Карло (QMC) интегрирования. Методов Монте-Карло часто используются для оценки сложных, многомерных интегралов без решения закрытой формы. QMC использует квазислучайные последовательности для улучшения свойств сходимости этих методов.
Космические экспериментальные проекты. Во многих экспериментальных настройках проведение измерений при каждой настройке фактора является дорогим или недопустимым. Квазислучайные последовательности обеспечивают эффективную, равномерную выборку проектного пространства.
Глобальная оптимизация. Алгоритмы оптимизации обычно находят локальный оптимум в окрестности начального значения. Используя квазислучайную последовательность начальных значений, ищет глобальную оптимальную равномерно выборочную области притяжения всех локальных минимумов.
Представьте простую последовательность 1-D, которая производит целые числа от 1 до 10. Это основная последовательность, и первые три точки [1,2,3]:
![]()
Теперь посмотрите, как Scramble, Skip, и Leap совместная работа:
Scramble - Скремблирование перетасовывает точки одним из нескольких различных способов. В этом примере предположим, что скрембл превращает последовательность в 1,3,5,7,9,2,4,6,8,10. Первые три точки сейчас [1,3,5]:
![]()
Skip - A Skip значение задает количество начальных точек, которые нужно игнорировать. В этом примере установите Skip значение 2. Последовательность теперь 5,7,9,2,4,6,8,10 и первые три точки [5,7,9]:
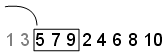
Leap - A Leap значение задает число точек, которые нужно игнорировать для каждой из них. Продолжение примера с Skip установите значение 2, если установите Leap чтобы 1, последовательность использует каждую другую точку. В этом примере последовательность теперь 5,9,4,8 и первые три точки [5,9,4]:
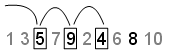
Функции Statistics and Machine Learning Toolbox™ поддерживают эти квазислучайные последовательности:
Halton sequences. Произведенное haltonset функция. Эти последовательности используют различные простые основы, чтобы сформировать последовательно более мелкие равномерные разбиения единичного интервала в каждой размерности.
Последовательности Соболь. Произведенное sobolset функция. Эти последовательности используют основу 2, чтобы сформировать последовательно более мелкие равномерные разбиения единичного интервала, и затем переупорядочивают координаты в каждой размерности.
Последовательности латинского гиперкуба. Произведенное lhsdesign функция. Хотя эти последовательности и не являются квазислучайными в смысле минимизации расхождений, тем не менее они дают разреженные однородные выборки, используемые в экспериментальных проектах.
Квазислучайные последовательности являются функциями от положительных целых чисел до модуля гиперкуба. Чтобы быть полезным в приложении, должна быть сгенерирована начальная point set последовательности. Наборы точек являются матрицами размера n -by - d, где n - число точек и d - размерность дискретизируемого гиперкуба. Функции haltonset и sobolset создать наборы точек со свойствами заданной квазислучайной последовательности. Начальные сегменты наборов точек генерируются net метод haltonset и sobolset классы, но точки могут быть сгенерированы и доступны в более общем случае с помощью индексации круглых скобок.
Из-за того, как генерируются квазислучайные последовательности, они могут содержать нежелательные корреляции, особенно в их начальных сегментах, и особенно в более высоких размерностях. Чтобы решить эту проблему, квазислучайные наборы точек часто skip, leap поверх или scramble значения в последовательности. The haltonset и sobolset функции позволяют вам задавать оба Skip и a Leap свойство квазислучайной последовательности и scramble метод haltonset и sobolset классы позволяют вам применять различные методы скремблирования. Скремблирование уменьшает корреляции, одновременно улучшая однородность.
В этом примере показано, как использовать haltonset чтобы создать 2-D квазислучайный набор точек Галтона.
Создайте haltonset p объекта, который пропускает первые 1000 значений последовательности и затем сохраняет каждую 101-ю точку.
rng default % For reproducibility p = haltonset(2,'Skip',1e3,'Leap',1e2)
p =
Halton point set in 2 dimensions (89180190640991 points)
Properties:
Skip : 1000
Leap : 100
ScrambleMethod : none
Объект p инкапсулирует свойства заданной квазислучайной последовательности. Набор точек конечен, длина определяется Skip и Leap свойства и по пределам размера индексов набора точек.
Использование scramble для применения реверсивного скремблирования.
p = scramble(p,'RR2')p =
Halton point set in 2 dimensions (89180190640991 points)
Properties:
Skip : 1000
Leap : 100
ScrambleMethod : RR2
Использование net чтобы сгенерировать первые 500 точек.
X0 = net(p,500);
Это эквивалентно
X0 = p(1:500,:);
Значения набора точек X0 не генерируются и хранятся в памяти, пока вы не получите доступ к p использование net или индексация круглых скобок.
Чтобы оценить природу квазислучайных чисел, создайте график поля точек из двух размерностей в X0.
scatter(X0(:,1),X0(:,2),5,'r') axis square title('{\bf Quasi-Random Scatter}')

Сравните это с рассеянием равномерных псевдослучайных чисел, сгенерированных rand функция.
X = rand(500,2); scatter(X(:,1),X(:,2),5,'b') axis square title('{\bf Uniform Random Scatter}')

Квазислучайный рассеяние выглядит более равномерным, избегая трения в псевдослучайном рассеянии.
В статистическом смысле квазислучайные числа являются слишком равномерными, чтобы пройти традиционные тесты случайности. Для примера тест Колмогорова-Смирнова, выполненный kstest, используется, чтобы оценить, имеет ли набор точек равномерное случайное распределение. При выполнении неоднократно на однородных псевдослучайных выборках, таких как сгенерированные randтест дает равномерное распределение p-значений.
nTests = 1e5; sampSize = 50; PVALS = zeros(nTests,1); for test = 1:nTests x = rand(sampSize,1); [h,pval] = kstest(x,[x,x]); PVALS(test) = pval; end histogram(PVALS,100) h = findobj(gca,'Type','patch'); xlabel('{\it p}-values') ylabel('Number of Tests')

Результаты являются совершенно различными, когда тест выполняется неоднократно на однородных квазислучайных выборках.
p = haltonset(1,'Skip',1e3,'Leap',1e2); p = scramble(p,'RR2'); nTests = 1e5; sampSize = 50; PVALS = zeros(nTests,1); for test = 1:nTests x = p(test:test+(sampSize-1),:); [h,pval] = kstest(x,[x,x]); PVALS(test) = pval; end histogram(PVALS,100) xlabel('{\it p}-values') ylabel('Number of Tests')

Маленькие p-значения ставят под вопрос нулевую гипотезу о том, что данные равномерно распределены. Если гипотеза верна, ожидается, что около 5% значений p опустится ниже 0,05. Результаты удивительно последовательны в их отказе оспорить гипотезу.
Квазислучайные streams, произведенные qrandstream function, используются для генерации последовательных квазислучайных выходов, а не наборов точек определенного размера. Потоки используются как pseudoRNGS, такие как rand, когда клиентским приложениям требуется источник квазислучайных чисел неопределенного размера, к которым можно периодически обращаться. Свойства квазислучайного потока, такого как его тип (Halton или Sobol), размерность, пропуск, скачок и скремблирование, задаются при построении потока.
В реализации квазислучайные потоки по существу являются очень большими квазислучайными наборами точек, хотя к ним обращаются по-разному. state квазислучайного потока является скалярным индексом следующей точки, которая будет взята из потока. Используйте qrand метод qrandstream класс для генерации точек из потока, начиная с текущего состояния. Используйте reset метод для сброса состояния в 1. В отличие от наборов точек, потоки не поддерживают индексацию круглых скобок.
В этом примере показано, как сгенерировать выборки из квазислучайного набора точек.
Использование haltonset для создания квазислучайного набора точек p, затем неоднократно увеличивайте индекс в набор точек test чтобы сгенерировать различные выборки.
p = haltonset(1,'Skip',1e3,'Leap',1e2); p = scramble(p,'RR2'); nTests = 1e5; sampSize = 50; PVALS = zeros(nTests,1); for test = 1:nTests x = p(test:test+(sampSize-1),:); [h,pval] = kstest(x,[x,x]); PVALS(test) = pval; end
Те же результаты получаются при помощи qrandstream чтобы создать квазислучайный поток q на основе набора точек p и позволяя потоку заботиться о шагах к индексу.
p = haltonset(1,'Skip',1e3,'Leap',1e2); p = scramble(p,'RR2'); q = qrandstream(p); nTests = 1e5; sampSize = 50; PVALS = zeros(nTests,1); for test = 1:nTests X = qrand(q,sampSize); [h,pval] = kstest(X,[X,X]); PVALS(test) = pval; end