В этом примере показано, как улучшить эффективность вентилятора охлаждения двигателя с помощью подхода Design for Six Sigma с помощью Define, Measure, Analyze, Improve, and Control (DMAIC). Первоначальный вентилятор не циркулирует достаточное количество воздуха через излучателя, чтобы сохранить охлаждение двигателя во время сложных условий. Во-первых, пример показывает, как спроектировать эксперимент, чтобы исследовать эффект трех факторов эффективности: расстояние вентилятора от излучателя, зазор кончика лезвия и угол тангажа блейда. Затем показано, как оценить оптимальные значения для каждого фактора, что приводит к проекту, который производит воздушные потоки сверх цели 875 ft3 в минуту с использованием тестовых данных. Наконец, он показывает, как использовать симуляции, чтобы убедиться, что новый проект производит воздушный поток согласно спецификациям более чем в 99,999% изготовленных вентиляторов. Этот пример использует MATLAB®, Statistics and Machine Learning Toolbox™, и Optimization Toolbox™.
Определите факторы, которые влияют на эффективность вентилятора
Управление производством улучшенного охлаждающего вентилятора
Этот пример относится к проекту вентилятора охлаждения двигателя, который не может вытащить достаточно воздуха через излучателя, чтобы поддерживать охлаждение двигателя во время сложных условий, таких как трафик остановки и движения или жаркая погода). Предположим, что вы оцениваете, что вам нужен воздушный поток не менее 875 футов3/ мин, чтобы сохранить двигатель холодным во время сложных условий. Необходимо оценить текущий проект и разработать альтернативный проект, который может достичь целевого воздушного потока.
Загрузите выборочные данные.
load(fullfile(matlabroot,'help/toolbox/stats/examples','OriginalFan.mat'))
Данные состоят из 10 000 измерений (исторические производственные данные) существующей эффективности вентиляторов охлаждения.
Постройте график данных для анализа эффективности текущего вентилятора.
plot(originalfan) xlabel('Observation') ylabel('Max Airflow (ft^3/min)') title('Historical Production Data')
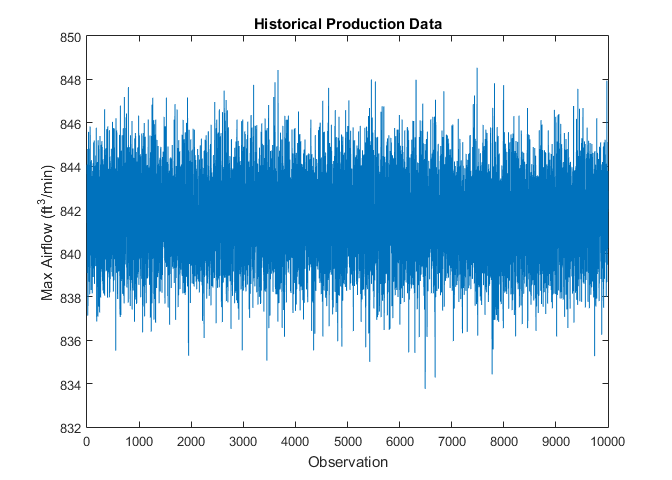
Данные центрированы вокруг 842 футов3/ мин и большинство значений находятся в области значений около 8 футов3/ мин. О базовом распределении данных, однако, график ничего не рассказывает. Постройте гистограмму и подбирайте нормальное распределение к данным.
figure() histfit(originalfan) % Plot histogram with normal distribution fit format shortg xlabel('Airflow (ft^3/min)') ylabel('Frequency (counts)') title('Airflow Histogram')
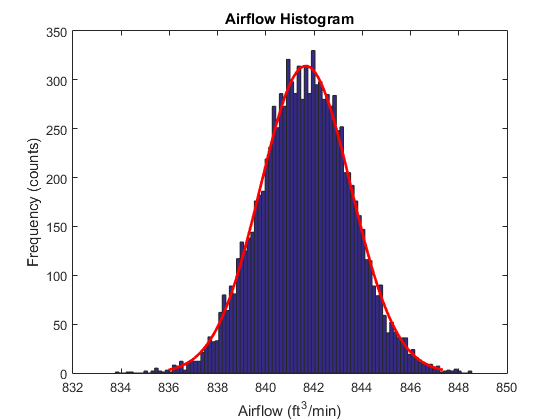
pd = fitdist(originalfan,'normal') % Fit normal distribution to data
pd =
NormalDistribution
Normal distribution
mu = 841.652 [841.616, 841.689]
sigma = 1.8768 [1.85114, 1.90318]
fitdist подходит для нормального распределения данных и оценивает параметры из данных. Оценка средней скорости воздушного потока составляет 841,652 фута3/ мин, и 95% доверительный интервал для средней скорости воздушного потока равен (841,616, 841,689). Эта оценка дает понять, что текущий вентилятор не близок к необходимому 875 ft3/ мин. Необходимо улучшить проект вентилятора, чтобы достичь целевого воздушного потока.
Оцените факторы, которые влияют на эффективность вентилятора охлаждения, используя проект экспериментов (DOE). Ответом является скорость потока воздуха вентилятора охлаждения (ft3/ мин). Предположим, что факторы, которые вы можете изменять и управлять:
Расстояние от излучателя
Угол тангажа
Зазор совета блейда
В целом гидросистемы имеют нелинейное поведение. Поэтому используйте проект поверхности отклика, чтобы оценить любые нелинейные взаимодействия среди факторов. Сгенерируйте экспериментальные запуски для проекта Box-Bhnken в закодированных (нормированных) переменных [-1, 0, + 1].
CodedValue = bbdesign(3)
CodedValue =
-1 -1 0
-1 1 0
1 -1 0
1 1 0
-1 0 -1
-1 0 1
1 0 -1
1 0 1
0 -1 -1
0 -1 1
0 1 -1
0 1 1
0 0 0
0 0 0
0 0 0
Первый столбец предназначен для расстояния от излучателя, второй столбец - для угла тангажа, а третий столбец - для зазора совета блейда. Предположим, что вы хотите протестировать эффекты переменных на следующих минимальных и максимальных значениях.
Расстояние от излучателя: от 1 до 1,5 дюйма
Угол тангажа: от 15 до 35 степени
Зазор совета блейда: от 1 до 2 дюймов
Рандомизируйте порядок запусков, преобразуйте закодированные проектные значения в реальные модули измерения и выполните эксперимент в заданном порядке.
runorder = randperm(15); % Random permutation of the runs bounds = [1 1.5;15 35;1 2]; % Min and max values for each factor RealValue = zeros(size(CodedValue)); for i = 1:size(CodedValue,2) % Convert coded values to real-world units zmax = max(CodedValue(:,i)); zmin = min(CodedValue(:,i)); RealValue(:,i) = interp1([zmin zmax],bounds(i,:),CodedValue(:,i)); end
Предположим, что в конце экспериментов вы собираете следующие значения отклика в переменной TestResult.
TestResult = [837 864 829 856 880 879 872 874 834 833 860 859 874 876 875]';
Отобразите проектные значения и ответ.
disp({'Run Number','Distance','Pitch','Clearance','Airflow'})
disp(sortrows([runorder' RealValue TestResult]))
'Run Number' 'Distance' 'Pitch' 'Clearance' 'Airflow'
1 1.5 35 1.5 856
2 1.25 25 1.5 876
3 1.5 25 1 872
4 1.25 25 1.5 875
5 1 35 1.5 864
6 1.25 25 1.5 874
7 1.25 15 2 833
8 1.5 15 1.5 829
9 1.25 15 1 834
10 1 15 1.5 837
11 1.5 25 2 874
12 1 25 1 880
13 1.25 35 1 860
14 1 25 2 879
15 1.25 35 2 859Сохраните проектные значения и ответ в table.
Expmt = table(runorder', CodedValue(:,1), CodedValue(:,2), CodedValue(:,3), ... TestResult,'VariableNames',{'RunNumber','D','P','C','Airflow'});
D означает Distance, P означает Pitch, и C означает Clearance. На основе результатов экспериментальных испытаний скорость воздушного потока чувствительна к изменяющимся значениям факторов. Кроме того, четыре экспериментальных запусков достигают или превышают целевую скорость воздушного потока 875 футов3/ min (выполняется 2, 4,12, и 14). Однако непонятно, какой, если какой, из этих запусков является оптимальным. В сложение не очевидно, насколько устойчива проект к изменениям в факторах. Создайте модель на основе текущих экспериментальных данных и используйте модель, чтобы оценить оптимальные настройки фактора.
Проект Box-Bennken позволяет вам протестировать нелинейные (квадратичные) эффекты. Форма квадратичной модели:
где AF - скорость воздушного потока, а Bi - коэффициент для термина i. Оцените коэффициенты этой модели, используя fitlm функция из набора инструментов Statistics and Machine Learning Toolbox.
mdl = fitlm(Expmt,'Airflow~D*P*C-D:P:C+D^2+P^2+C^2');Отобразите величины коэффициентов (для нормированных значений) на столбчатой диаграмме.
figure() h = bar(mdl.Coefficients.Estimate(2:10)); set(h,'facecolor',[0.8 0.8 0.9]) legend('Coefficient') set(gcf,'units','normalized','position',[0.05 0.4 0.35 0.4]) set(gca,'xticklabel',mdl.CoefficientNames(2:10)) ylabel('Airflow (ft^3/min)') xlabel('Normalized Coefficient') title('Quadratic Model Coefficients')
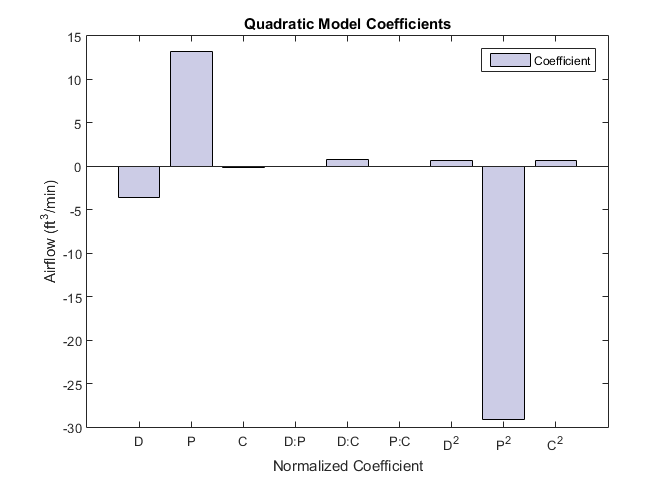
Столбчатая диаграмма показывает, что Pitch и Pitch2 являются доминирующими факторами. Можно просмотреть отношение между несколькими входными переменными и одной выходной переменной, сгенерировав объемную поверхностную диаграмму отклика. Использование plotSlice чтобы сгенерировать объемные поверхностные диаграммы отклика для модели mdl в интерактивном режиме.
plotSlice(mdl)
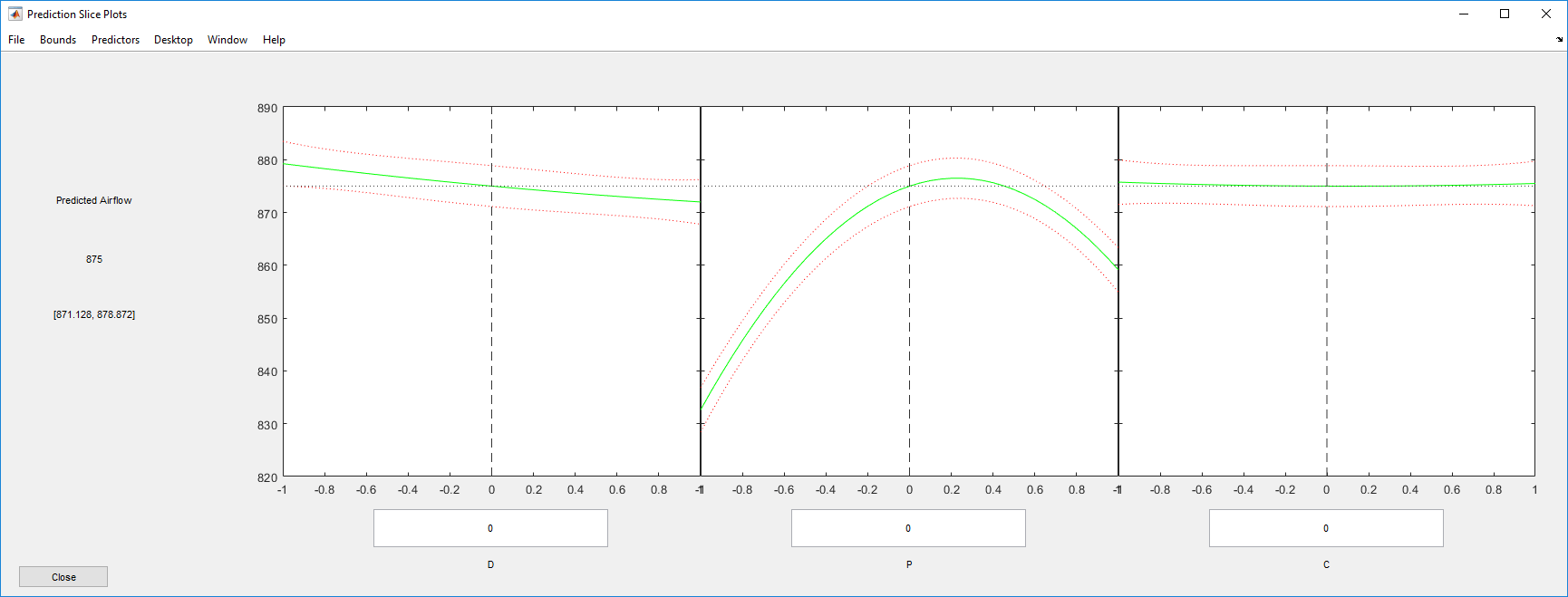
График показывает нелинейное соотношение воздушного потока с тангажом. Переместите синие штриховые линии вокруг и увидите эффект различных факторов на воздушный поток. Хотя можно использовать plotSlice чтобы определить оптимальные настройки фактора, можно также использовать Optimization Toolbox, чтобы автоматизировать задачу.
Найдите оптимальные настройки фактора, используя оптимизационную функцию fmincon.
Напишите целевую функцию.
f = @(x) -x2fx(x,'quadratic')*mdl.Coefficients.Estimate;Целевая функция является квадратичной поверхностью отклика, подгоняемой к данным. Минимизация отрицательного воздушного потока с помощью fmincon является тем же самым, что и максимизация исходной целевой функции. Ограничениями являются проверенные верхний и нижний пределы (в закодированных значениях). Установите начальную начальную точку в центр проекта экспериментальной тестовой матрицы.
lb = [-1 -1 -1]; % Lower bound ub = [1 1 1]; % Upper bound x0 = [0 0 0]; % Starting point [optfactors,fval] = fmincon(f,x0,[],[],[],[],lb,ub,[]); % Invoke the solver
Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the default value of the function tolerance, and constraints are satisfied to within the default value of the constraint tolerance.
Преобразуйте результаты в задачу максимизации и реальные модули.
maxval = -fval; maxloc = (optfactors + 1)'; bounds = [1 1.5;15 35;1 2]; maxloc=bounds(:,1)+maxloc .* ((bounds(:,2) - bounds(:,1))/2); disp('Optimal Values:') disp({'Distance','Pitch','Clearance','Airflow'}) disp([maxloc' maxval])
Optimal Values:
'Distance' 'Pitch' 'Clearance' 'Airflow'
1 27.275 1 882.26Результат оптимизации предполагает размещение нового вентилятора на один дюйм от излучателя с однодюймовым зазором между советами блейдов вентилятора и кожухом.
Поскольку угол тангажа оказывает столь значительный эффект на воздушный поток, выполните дополнительный анализ, чтобы убедиться, что угол тангажа 27,3 степеней оптимален.
load(fullfile(matlabroot,'help/toolbox/stats/examples','AirflowData.mat')) tbl = table(pitch,airflow); mdl2 = fitlm(tbl,'airflow~pitch^2'); mdl2.Rsquared.Ordinary
ans =
0.99632
Результаты показывают, что квадратичная модель объясняет эффект тангажа на скважину воздушного потока.
Постройте график угла тангажа относительно воздушного потока и наложите подобранную модель.
figure() plot(pitch,airflow,'.r') hold on ylim([840 885]) line(pitch,mdl2.Fitted,'color','b') title('Fitted Model and Data') xlabel('Pitch angle (degrees)') ylabel('Airflow (ft^3/min)') legend('Test data','Quadratic model','Location','se') hold off
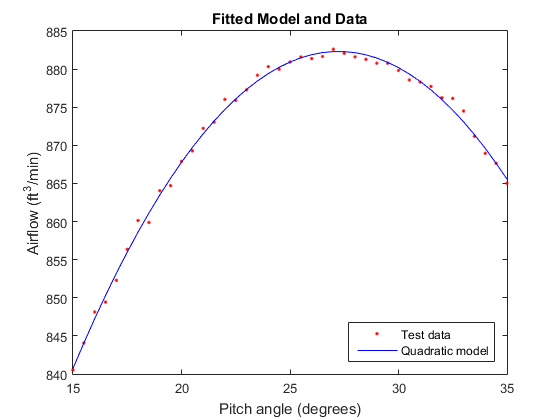
Найдите значение тангажа, которое соответствует максимальному потоку воздуха.
pitch(find(airflow==max(airflow)))
ans =
27Дополнительный анализ подтверждает, что угол тангажа 27,3 степеней оптимален.
Улучшенный проект охлаждающего вентилятора соответствует требованиям к воздушному потоку. У вас также есть модель, которая хорошо аппроксимирует эффективность вентилятора на основе факторов, которые можно изменить в проекте. Убедитесь, что эффективность вентилятора устойчива к изменчивости в производстве и установке, выполнив анализ чувствительности.
Предположим, что, основываясь на историческом опыте, производственная неопределенность заключается в следующем.
| Фактор | Действительные значения | Закодированные значения |
|---|---|---|
| Расстояние от излучателя | 1,00 +/- 0,05 дюйма | 1,00 +/- 0,20 дюйма |
| Угол тангажа блейда | 27,3 +/- 0,25 степени | 0.227 +/- 0.028 степени |
| Зазор совета блейда | 1,00 +/- 0,125 дюйма | -1.00 +/- 0,25 дюйма |
Проверьте, что эти изменения факторов позволят поддерживать устойчивый проект вокруг целевого воздушного потока. Философия Six Sigma нацелена на частоту дефектов не более 3,4 на 1 000 000 вентиляторов. То есть болельщики должны поразить 875 футов3/ мин целевое 99,999% времени.
Можно проверить проект с помощью симуляции Монте-Карло. Сгенерируйте 10000 случайных чисел для трех факторов с заданным допуском. Во-первых, установите состояние генераторов случайных чисел, чтобы результаты были последовательными для различных запусков.
rng('default')Выполните симуляцию Монте-Карло. Включите переменную шума, которая пропорциональна шуму в подобранной модели, mdl (то есть ошибка RMS модели). Поскольку коэффициенты модели находятся в закодированных переменных, вы должны сгенерировать dist, pitch, и clearance использование кодированного определения.
dist = random('normal',optfactors(1),0.20,[10000 1]); pitch = random('normal',optfactors(2),0.028,[10000 1]); clearance = random('normal',optfactors(3),0.25,[10000 1]); noise = random('normal',0,mdl2.RMSE,[10000 1]);
Вычислите воздушный поток для 10000 комбинаций случайных факторов с помощью модели.
simfactor = [dist pitch clearance];
X = x2fx(simfactor,'quadratic');Добавьте шум в модель (изменение в данных, которое модель не учитывала).
simflow = X*mdl.Coefficients.Estimate+noise;
Оцените изменение предсказанного воздушного потока модели с помощью гистограммы. Чтобы оценить среднее и стандартное отклонение, подбирайте нормальное распределение к данным.
pd = fitdist(simflow,'normal'); histfit(simflow) hold on text(pd.mu+2,300,['Mean: ' num2str(round(pd.mu))]) text(pd.mu+2,280,['Standard deviation: ' num2str(round(pd.sigma))]) hold off xlabel('Airflow (ft^3/min)') ylabel('Frequency') title('Monte Carlo Simulation Results')
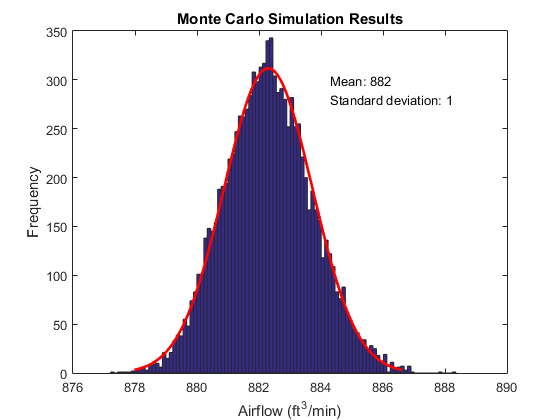
Результаты выглядят многообещающими. Средний воздушный поток составляет 882 футов3/ мин и, по-видимому, лучше 875 футов3/ min для большей части данных .
Определите вероятность того, что воздушный поток на уровне 875 футов3/ мин или ниже.
format long
pfail = cdf(pd,875)
pass = (1-pfail)*100pfail =
1.509289008603141e-07
pass =
99.999984907109919По-видимому, проект достигает по меньшей мере 875 футов3/ мин воздушного потока 99,999% времени.
Используйте результаты симуляции, чтобы оценить возможности процесса.
S = capability(simflow,[875.0 890]) pass = (1-S.Pl)*100
S =
mu: 8.822982645666709e+02
sigma: 1.424806876923940
P: 0.999999816749816
Pl: 1.509289008603141e-07
Pu: 3.232128339675335e-08
Cp: 1.754623760237126
Cpl: 1.707427788957002
Cpu: 1.801819731517250
Cpk: 1.707427788957002
pass =
99.9999849071099The Cp значение равно 1,75. Процесс рассматривается как высококачественный при Cp больше или равно 1,6. The Cpk аналогичен Cp значение, которое указывает, что процесс центрирован. Теперь реализуйте этот проект. Контролируйте его, чтобы проверить процесс проекта и убедиться, что охлаждающий вентилятор обеспечивает высококачественную эффективность.
Можно контролировать и оценивать процесс производства и установки нового вентилятора с помощью диаграмм управления. Оцените первые 30 дней производства нового охлаждающего вентилятора. Первоначально выпускалось пять охлаждающих вентиляторов в день. Во-первых, загрузите выборочные данные из нового процесса.
load(fullfile(matlabroot,'help/toolbox/stats/examples','spcdata.mat'))
Постройте график X -bar и S графиков.
figure() controlchart(spcflow,'chart',{'xbar','s'}) % Reshape the data into daily sets xlabel('Day')
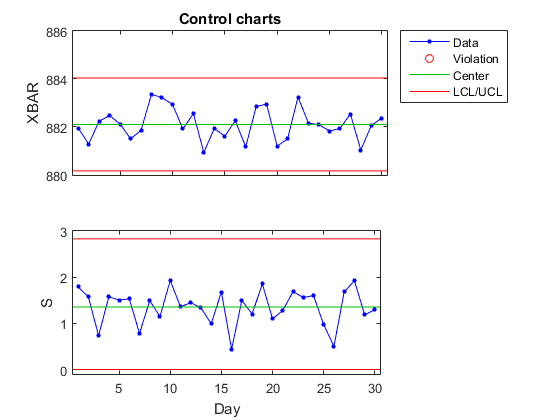
Согласно результатам, производственный процесс находится в статистическом контроле, на что указывает отсутствие нарушений контрольных пределов или неслучайных шаблонов в данных с течением времени. Для анализа процесса можно также запустить анализ возможностей на данных.
[row,col] = size(spcflow); S2 = capability(reshape(spcflow,row*col,1),[875.0 890]) pass = (1-S.Pl)*100
S2 =
mu: 8.821061141685465e+02
sigma: 1.423887508874697
P: 0.999999684316149
Pl: 3.008932155898586e-07
Pu: 1.479063578225176e-08
Cp: 1.755756676295137
Cpl: 1.663547652525458
Cpu: 1.847965700064817
Cpk: 1.663547652525458
pass =
99.9999699106784
The Cp значение 1.755 очень похоже на расчетное значение 1.73. The Cpk значение 1.66 меньше Cp значение. Однако только Cpk значение менее 1,33, что указывает на то, что процесс значительно сместился к одному из пределов процесса, является проблемой. Процесс находится в пределах, и он достигает целевого воздушного потока (875 футов)3/ мин) более 99,999% времени.