loss

Потеря наивной модели классификации Байеса для инкрементного обучения на пакете данных

Синтаксис

L = loss(Mdl,X,Y)

L = loss(Mdl,X,Y,Name,Value)

Описание

loss возвращает классификационную потерю сконфигурированной наивной классификационной модели Байеса для модели инкрементного обучения (incrementalClassificationNaiveBayes объект).

Чтобы измерить производительность модели в потоке данных и сохранить результаты в модели выхода, вызовите updateMetrics или updateMetricsAndFit.

пример

L = loss(Mdl,X,Y) возвращает минимальные потери классификации затрат для наивной модели классификации Байеса для инкрементного обучения Mdl использование пакета данных предиктора X и соответствующие ответы Y.

пример

L = loss(Mdl,X,Y,Name,Value) использует дополнительные опции, заданные одним или несколькими аргументами пары "имя-значение". Например, можно задать функцию классификационных потерь.

Примеры

свернуть все

Измерьте производительность модели во время инкрементного обучения

Открыть Live Script

Эффективность инкрементальной модели на потоковых данных измеряется тремя способами:

Кумулятивные метрики измеряют эффективность с начала инкрементного обучения.
Метрики окна измеряют эффективность в заданном окне наблюдений. Метрики обновляются каждый раз, когда модель обрабатывает указанное окно.
The loss функция измеряет эффективность только для заданного пакета данных.

Загрузите набор данных о деятельности человека. Случайным образом перетасуйте данные.

load humanactivity
n = numel(actid);
rng(1); % For reproducibility
idx = randsample(n,n);
X = feat(idx,:);
Y = actid(idx);

Для получения дополнительной информации о наборе данных введите Description в командной строке.

Создайте наивную модель классификации Байеса для инкрементного обучения; задайте имена классов и размер окна метрики 1000 наблюдений. Сконфигурируйте его для loss подгонкой к первым 10 наблюдениям.

Mdl = incrementalClassificationNaiveBayes('ClassNames',unique(Y),'MetricsWindowSize',1000);
initobs = 10;
Mdl = fit(Mdl,X(1:initobs,:),Y(1:initobs));
canComputeLoss = (size(Mdl.DistributionParameters,2) == Mdl.NumPredictors) +...
    (size(Mdl.DistributionParameters,1) > 1) > 1

canComputeLoss = logical
   1

Mdl является incrementalClassificationLinear модель. Все его свойства доступны только для чтения.

Симулируйте поток данных и выполните следующие действия на каждом входящем фрагменте из 50 наблюдений:

Функции updateMetrics для измерения совокупной эффективности и эффективности в окне наблюдений. Перезаписать предыдущую инкрементальную модель на новую для отслеживания показателей эффективности.
Функции loss для измерения производительности модели на входящем фрагменте.
Функции fit для подгонки модели к входящему фрагменту. Перезаписать предыдущую инкрементальную модель на новую, подобранную входящему наблюдению.
Сохраните все метрики эффективности, чтобы увидеть, как они развиваются во время инкрементного обучения.

% Preallocation
numObsPerChunk = 500;
nchunk = floor((n - initobs)/numObsPerChunk);
mc = array2table(zeros(nchunk,3),'VariableNames',["Cumulative" "Window" "Loss"]);

% Incremental learning
for j = 1:nchunk
    ibegin = min(n,numObsPerChunk*(j-1) + 1 + initobs);
    iend   = min(n,numObsPerChunk*j + initobs);
    idx = ibegin:iend;    
    Mdl = updateMetrics(Mdl,X(idx,:),Y(idx));
    mc{j,["Cumulative" "Window"]} = Mdl.Metrics{"MinimalCost",:};
    mc{j,"Loss"} = loss(Mdl,X(idx,:),Y(idx));
    Mdl = fit(Mdl,X(idx,:),Y(idx));
end

Mdl является incrementalClassificationNaiveBayes объект модели обучен на всех данных в потоке. Во время инкрементного обучения и после прогрева модели updateMetrics проверяет эффективность модели при входящем наблюдении, затем и fit функция соответствует модели этому наблюдению. loss является агностическим для периода прогрева метрики, поэтому измеряет минимальные затраты для всех итераций.

Чтобы увидеть, как метрики эффективности развивались во время обучения, постройте их.

figure;
plot(mc.Variables);
xlim([0 nchunk]);
ylim([0 0.1])
ylabel('Minimal Cost')
xline(Mdl.MetricsWarmupPeriod/numObsPerChunk + 1,'r-.');
legend(mc.Properties.VariableNames)
xlabel('Iteration')

В течение периода прогрева метрики (область слева от красной линии) желтая линия представляет минимальные затраты на каждый входящий фрагмент данных. После периода прогрева метрики Mdl отслеживает совокупные и оконные метрики. Совокупные и пакетные потери сходятся как fit функция подходит для инкрементальной модели к входящим данным.

Вычисление пользовательских потерь на входящих фрагментах данных

Открыть Live Script

Подгонка наивной модели классификации Байеса для инкрементного обучения к потоковым данным и вычисление многоклассовой потери перекрестной энтропии на входящих фрагментах данных.

Загрузите набор данных о деятельности человека. Случайным образом перетасуйте данные.

load humanactivity
n = numel(actid);
rng(1); % For reproducibility
idx = randsample(n,n);
X = feat(idx,:);
Y = actid(idx);

Для получения дополнительной информации о наборе данных введите Description в командной строке.

Создайте наивную модель классификации Байеса для инкрементного обучения. Сконфигурируйте модель следующим образом:

Задайте имена классов
Задайте период прогрева метрики 1000 наблюдений.
Задайте размер окна метрики 2000 наблюдений.
Отслеживайте многоклассовые потери перекрестной энтропии, чтобы измерить эффективность модели. Создайте анонимную функцию, которая измеряет многоклассовую потерю перекрестной энтропии каждого нового наблюдения, включают допуск на числовую стабильность. Создайте массив структур, содержащий имя CrossEntropy и ее соответствующую функцию.
Сконфигурируйте модель, чтобы вычислить потери классификации, подгоняя модель к первым 10 наблюдениям.

tolerance = 1e-10;
crossentropy = @(z,zfit,w,cost)-log(max(zfit(z),tolerance));
ce = struct("CrossEntropy",crossentropy);

Mdl = incrementalClassificationNaiveBayes('ClassNames',unique(Y),'MetricsWarmupPeriod',1000,...
    'MetricsWindowSize',2000,'Metrics',ce);
initobs = 10;
Mdl = fit(Mdl,X(1:initobs,:),Y(1:initobs));

Mdl является incrementalClassificationNaiveBayes объект модели, сконфигурированный для инкрементного обучения.

Выполните инкрементальное обучение. При каждой итерации:

Симулируйте поток данных путем обработки фрагмента 100 наблюдений.
Функции updateMetrics вычислить совокупные и оконные метрики на входящем фрагменты данных. Перезаписать предыдущую инкрементальную модель на новую, подобранную для перезаписи предыдущих метрик.
Функции loss для вычисления перекрестной энтропии на входящем фрагменты данных. В то время как совокупная и оконная метрики требуют, чтобы пользовательские потери возвращали потери для каждого наблюдения, loss требуется потеря всего фрагмента. Вычислите среднее значение потерь в фрагменте.
Функции fit для подгонки инкрементальной модели к входящему фрагменту данных.
Сохраните совокупные, оконные и частичные метрики, чтобы увидеть, как они развиваются во время инкрементного обучения.

% Preallocation
numObsPerChunk = 100;
nchunk = floor((n - initobs)/numObsPerChunk);
tanloss = array2table(zeros(nchunk,3),'VariableNames',["Cumulative" "Window" "Chunk"]);

% Incremental fitting
for j = 1:nchunk
    ibegin = min(n,numObsPerChunk*(j-1) + 1 + initobs);
    iend   = min(n,numObsPerChunk*j + initobs);
    idx = ibegin:iend;    
    Mdl = updateMetrics(Mdl,X(idx,:),Y(idx));
    tanloss{j,1:2} = Mdl.Metrics{"CrossEntropy",:};
    tanloss{j,3} = loss(Mdl,X(idx,:),Y(idx),'LossFun',@(z,zfit,w,cost)mean(crossentropy(z,zfit,w,cost)));
    Mdl = fit(Mdl,X(idx,:),Y(idx));
end

IncrementalMdl является incrementalClassificationNaiveBayes объект модели обучен на всех данных в потоке. Во время инкрементного обучения и после прогрева модели updateMetrics проверяет эффективность модели при входящем наблюдении и fit функция соответствует модели этому наблюдению.

Постройте график показателей эффективности, чтобы увидеть, как они развивались во время инкрементного обучения.

figure;
h = plot(tanloss.Variables);
ylabel('Cross Entropy')
xline(Mdl.MetricsWarmupPeriod/numObsPerChunk,'r-.');
xlabel('Iteration')
legend(h,tanloss.Properties.VariableNames)

График предполагает следующее:

updateMetrics вычисляет показатели эффективности только после периода прогрева метрики.
updateMetrics вычисляет совокупные метрики во время каждой итерации.
updateMetrics вычисляет метрики окна после обработки 100 наблюдений
Потому что Mdl был сконфигурирован так, чтобы предсказывать наблюдения с начала инкрементного обучения, loss может вычислить перекрестную энтропию для каждого входящего фрагмента данных.

Входные параметры

свернуть все

`Mdl` - Наивная классификационная модель Байеса для инкрементного обучения
`incrementalClassificationNaiveBayes` объект модели

Наивная модель классификации Байеса для инкрементного обучения, заданная как incrementalClassificationNaiveBayes объект модели. Можно создавать Mdl непосредственно или путем преобразования поддерживаемой, традиционно обученной модели машинного обучения с помощью incrementalLearner функция. Для получения дополнительной информации см. соответствующую страницу с описанием.

Необходимо сконфигурировать Mdl вычислить его потери по пакету наблюдений.

Если Mdl является преобразованной, традиционно обученной моделью, вычислить ее потерю можно без каких-либо изменений.
В противном случае необходимо подогнать модель входа Mdl к данным, которые содержали все ожидаемые классы (Mdl.DistributionParameters должна быть матрицей камер с Mdl.NumPredictors столбцы и, по крайней мере, одна строка, где каждая строка соответствует каждому имени класса в Mdl.ClassNames).

`X` - Пакет данных предиктора
матрица с плавающей точкой

Пакет данных предиктора, с помощью которых можно вычислить потерю, заданный как n -by- Mdl.NumPredictors матрица с плавающей точкой.

Длина меток наблюдений Y и количество наблюдений в X должна быть равной; Y (j) - метка j наблюдения (строка или столбец) в X.

Примечание

loss поддерживает только входные данные предиктора с плавающей точкой. Если модель входа Mdl представляет собой преобразованную, традиционно обученную модель, подходящую для категориальных данных, использование dummyvar чтобы преобразовать каждую категориальную переменную в числовую матрицу фиктивных переменных и объединить все фиктивные переменные матрицы и любые другие числовые предикторы. Для получения дополнительной информации см. Dummy Переменных.

Типы данных: single | double

`Y` - Партия меток
категориальный массив | символьный массив | строковые массивы | логический вектор | вектор с плавающей точкой | массив ячеек из векторов символов

Пакет меток, с помощью которых можно вычислить потерю, заданный как категориальные символьные или строковые массивы, логический вектор или вектор с плавающей точкой или массив ячеек векторов символов для задач классификации; или вектор с плавающей точкой для регрессионных задач.

Когда ClassNames свойство модели входа Mdl не пуст, применяются следующие условия:
- Если Y содержит метку, которая не является представителем Mdl.ClassNames, loss выдает ошибку.
- Тип данных Y и Mdl.ClassNames должно быть то же самое.

Аргументы в виде пар имя-значение

Задайте необязательные разделенные разделенными запятой парами Name,Value аргументы. Name - имя аргумента и Value - соответствующее значение. Name должны находиться внутри кавычек. Можно задать несколько аргументов в виде пар имен и значений в любом порядке Name1,Value1,...,NameN,ValueN.

Пример: 'LossFun','classiferror','Weights',W задает возврат частоты ошибок неправильной классификации и весов наблюдений W.

`'LossFun'` - Функция потерь
`'mincost'` (дефолт) | натягивает вектор | указатель на функцию | вектор камеры | массив структур |...

Функция потерь, заданная как встроенное имя функции потерь или указатель на функцию.

В следующей таблице перечислены встроенные имена функции потерь. Можно задать больше одного при помощи строкового вектора.

Имя	Описание
`"binodeviance"`	Биномиальное отклонение
`"classiferror"`	Вероятность ошибки неправильной классификации
`"exponential"`	Экспоненциал
`"hinge"`	Стержень
`"logit"`	Логистический
'`"mincost"`	Минимальные ожидаемые затраты на неправильную классификацию
`"quadratic"`	Квадратный

Для получения дополнительной информации смотрите Классификационные потери.

Чтобы задать пользовательскую функцию потерь, используйте обозначение указателя на функцию. Функция должна иметь следующую форму:

lossval = lossfcn(C,S,W,Cost)

Выходной аргумент lossval - вектор с n -by-1 с плавающей точкой, где lossval (j) классификационная потеря наблюдений j.
Вы задаете имя функции (lossfcn).
C является n -by-2 логической матрицей с строками, указывающими класс, к которому принадлежит соответствующее наблюдение. Порядок столбцов соответствует порядку классов в ClassNames свойство. Создание C путем установки C (p, q) = 1, если наблюдение p находится в q классов, для каждого наблюдения в заданных данных. Установите другой элемент в строку p на 0.
S является n -by-2 числовой матрицей предсказанных классификационных оценок. S аналогичен Posterior выхода predict, где строки соответствуют наблюдениям в данных, а порядок столбцов соответствует порядку классов в ClassNames свойство. S (p, q) - классификационная оценка наблюдения p классифицируется в классах q.
W является n -by-1 числовым вектором весов наблюдений.
Cost является K -by K числовой матрицей затрат на неправильную классификацию.

Пример: 'LossFun',"classiferror"

Пример: 'LossFun', @ lossfcn

Типы данных: char | string | function_handle

`'Weights'` - Фрагмент весов наблюдений
вектор положительных значений с плавающей точкой

Фрагмент весов наблюдений, заданный как вектор с плавающей точкой положительных значений. loss взвешивает наблюдения в X с соответствующими значениями в Weights. Размер Weights должен равняться n, это количество наблюдений в X.

По умолчанию Weights это таковые (n,1).

Для получения дополнительной информации, включая схемы нормализации, см. «Веса наблюдений».

Типы данных: double | single

Выходные аргументы

свернуть все

`L` - Классификационные потери
числовой скаляр

Классификационные потери, возвращенные как числовой скаляр. L является мерой качества модели. Его интерпретация зависит от функции потерь и схемы взвешивания.

Подробнее о

свернуть все

Классификационные потери

Classification loss функции измеряют прогнозирующую неточность классификационных моделей. Когда вы сравниваете один и тот же тип потерь среди многих моделей, более низкая потеря указывает на лучшую прогнозирующую модель.

Рассмотрим следующий сценарий.

L - средневзвешенные классификационные потери.
n - размер выборки.
Для двоичной классификации:
- _yj - наблюдаемая метка класса. Программное обеспечение кодирует его как -1 или 1, указывая на отрицательный или положительный класс (или первый или второй класс в ClassNames свойство), соответственно.
- f (_Xj) является баллом классификации положительного класса для j наблюдений (строка) X данных предиктора.
- _mj = _yj f ₍Xj) является классификационной оценкой для классификации j наблюдений в класс, относящийся к yj. Положительные значения mj указывают на правильную классификацию и не вносят большой вклад в средние потери. Отрицательные значения mj указывают на неправильную классификацию и вносят значительный вклад в среднюю потерю.
Для алгоритмов, которые поддерживают многоклассовую классификацию (то есть K ≥ 3):
- _yj^* - вектор с K - 1 нулями, с 1 в положении, соответствующем истинному, наблюдаемому классу _yj. Для примера, если истинный класс второго наблюдения является третьим классом и K = 4, то y 2^* = [0 0 1 0]′. Порядок классов соответствует порядку в ClassNames свойство модели входа.
- f (_Xj) является вектором K длины счетов классов для j наблюдений X данных предиктора. Порядок счетов соответствует порядку классов в ClassNames свойство модели входа.
- _mj = _yj^*′ f _{(<reservedrangesplaceholder1>)}. Поэтому mj является скалярной классификационной оценкой, которую модель предсказывает для истинного наблюдаемого класса.
Вес для j наблюдения _wj. Программа нормализует веса наблюдений так, чтобы они суммировались с соответствующей вероятностью предыдущего класса. Программное обеспечение также нормализует предыдущие вероятности, поэтому они равны 1. Поэтому,

$\sum_{j = 1}^{n} w_{j} = 1.$

С учетом этого сценария в следующей таблице описываются поддерживаемые функции потерь, которые можно задать при помощи 'LossFun' аргумент пары "имя-значение".

Функция потерь	Значение `LossFun`	Уравнение
Биномиальное отклонение	`'binodeviance'`	$L = \sum_{j = 1}^{n} w_{j} \log {1 + \exp [- 2 m_{j}]} .$
Неверно классифицированный коэффициент в десятичных числах	`'classiferror'`	$L = \sum_{j = 1}^{n} w_{j} I {{\hat{y}}_{j} \neq y_{j}} .$ ${\hat{y}}_{j}$ - метка класса, соответствующая классу с максимальным счетом. I {·} является функцией индикации.
Потери перекрестной энтропии	`'crossentropy'`	`'crossentropy'` подходит только для моделей нейронных сетей. Взвешенные потери перекрестной энтропии $L = - \sum_{j = 1}^{n} \frac{{\tilde{w}}_{j} \log (m_{j})}{K n},$ где веса ${\tilde{w}}_{j}$ нормированы в сумме к n вместо 1.
Экспоненциальные потери	`'exponential'`	$L = \sum_{j = 1}^{n} w_{j} \exp (- m_{j}) .$
Потеря шарнира	`'hinge'`	$L = \sum_{j = 1}^{n} w_{j} \max {0, 1 - m_{j}} .$
Логит потеря	`'logit'`	$L = \sum_{j = 1}^{n} w_{j} \log (1 + \exp (- m_{j})) .$
Минимальные ожидаемые затраты на неправильную классификацию	`'mincost'`	`'mincost'` подходит только, если классификационные оценки апостериорные вероятности. Программа вычисляет взвешенные минимальные ожидаемые затраты классификации, используя эту процедуру для наблюдений j = 1,..., n. Оцените ожидаемые затраты на неправильную классификацию классификации _Xj наблюдений в k классов: $γ_{j k} = {(f {(X_{j})}^{'} C)}_{k} .$ f (_Xj) является вектором-столбцом апостериорных вероятностей классов для двоичной и многоклассовой классификации для _Xj наблюдений. C - матрица затрат, сохраненная в `Cost` свойство модели. Для j наблюдения спрогнозируйте метку класса, соответствующую минимальной ожидаемой стоимости неправильной классификации: ${\hat{y}}_{j} = \underset{k = 1, ..., K}{argmin} γ_{j k} .$ Используя C, идентифицируйте понесенные затраты (_cj) для создания предсказания. Взвешенное среднее значение минимальных ожидаемых потерь от неправильной классификации $L = \sum_{j = 1}^{n} w_{j} c_{j} .$ Если вы используете матрицу затрат по умолчанию (значение элемента которой 0 для правильной классификации и 1 для неправильной классификации), то `'mincost'` потеря эквивалентна `'classiferror'` потеря.
Квадратичные потери	`'quadratic'`	$L = \sum_{j = 1}^{n} w_{j} {(1 - m_{j})}^{2} .$

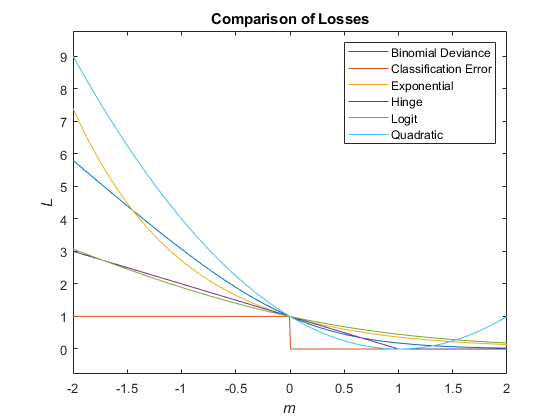
Этот рисунок сравнивает функции потерь (кроме 'crossentropy' и 'mincost') по счету m для одного наблюдения. Некоторые функции нормированы, чтобы пройти через точку (0,1).

Алгоритмы

свернуть все

Веса наблюдений

Для каждого условного распределения предиктора, loss вычисляет взвешенные средние значения и стандартное отклонение.

Если известное распределение вероятностей классов (другими словами, предшествующее распределение не эмпирическое), loss нормализует веса наблюдений в сумме с предшествующими вероятностями классов в соответствующих классах. Это действие подразумевает, что веса наблюдений по умолчанию являются соответствующими вероятностями предыдущего класса.

Если распределение вероятностей предыдущего класса эмпирическое, программное обеспечение нормализует указанные веса наблюдений до суммы 1 каждый раз, когда вы вызываете loss.

Документация

loss

Синтаксис

Описание

Примеры

Измерьте производительность модели во время инкрементного обучения

Вычисление пользовательских потерь на входящих фрагментах данных

Входные параметры

`Mdl` - Наивная классификационная модель Байеса для инкрементного обучения
`incrementalClassificationNaiveBayes` объект модели

`X` - Пакет данных предиктора
матрица с плавающей точкой

`Y` - Партия меток
категориальный массив | символьный массив | строковые массивы | логический вектор | вектор с плавающей точкой | массив ячеек из векторов символов

Аргументы в виде пар имя-значение

`'LossFun'` - Функция потерь
`'mincost'` (дефолт) | натягивает вектор | указатель на функцию | вектор камеры | массив структур |...

`'Weights'` - Фрагмент весов наблюдений
вектор положительных значений с плавающей точкой

Выходные аргументы

`L` - Классификационные потери
числовой скаляр

Подробнее о

Классификационные потери

Алгоритмы

Веса наблюдений

См. также

Объекты

Функции

Темы

Statistics and Machine Learning Toolbox документация

Поддержка

Документация

loss

Синтаксис

Описание

Примеры

Измерьте производительность модели во время инкрементного обучения

Вычисление пользовательских потерь на входящих фрагментах данных

Входные параметры

Mdl - Наивная классификационная модель Байеса для инкрементного обучения incrementalClassificationNaiveBayes объект модели

X - Пакет данных предиктора матрица с плавающей точкой

Y - Партия меток категориальный массив | символьный массив | строковые массивы | логический вектор | вектор с плавающей точкой | массив ячеек из векторов символов

Аргументы в виде пар имя-значение

'LossFun' - Функция потерь 'mincost' (дефолт) | натягивает вектор | указатель на функцию | вектор камеры | массив структур |...

'Weights' - Фрагмент весов наблюдений вектор положительных значений с плавающей точкой

Выходные аргументы

L - Классификационные потери числовой скаляр

Подробнее о

Классификационные потери

Алгоритмы

Веса наблюдений

См. также

Объекты

Функции

Темы

Statistics and Machine Learning Toolbox документация

Поддержка

`Mdl` - Наивная классификационная модель Байеса для инкрементного обучения
`incrementalClassificationNaiveBayes` объект модели

`X` - Пакет данных предиктора
матрица с плавающей точкой

`Y` - Партия меток
категориальный массив | символьный массив | строковые массивы | логический вектор | вектор с плавающей точкой | массив ячеек из векторов символов

`'LossFun'` - Функция потерь
`'mincost'` (дефолт) | натягивает вектор | указатель на функцию | вектор камеры | массив структур |...

`'Weights'` - Фрагмент весов наблюдений
вектор положительных значений с плавающей точкой

`L` - Классификационные потери
числовой скаляр