Интегрирование

Если f является символическим выражением, тогда

int(f)

пытается найти другое символическое выражение, F, так что diff(F) = f. То есть int(f) возвращает неопределенный интеграл или антипроизводную f (при условии, что он существует в закрытой форме). Подобно дифференциации,

int(f,v)

использует символьный объект v как переменная интегрирования, а не как переменная, определяемая symvar. Посмотрите, как int работает, глядя на эту таблицу.

Математическая операция	MATLAB^® Команда
$\int x^{n} d x = {\begin{array}{l} \log (x) & если n = - 1 \\ \frac{x^{n + 1}}{n + 1} & иначе . \end{array}$	`int(x^n)` или `int(x^n,x)`
$\int_{0}^{π / 2} \sin (2 x) d x = 1$	`int(sin(2x), 0, pi/2)` или `int(sin(2x), x, 0, pi/2)`
g = cos (at + b) $\int g (t) d t = \sin (a t + b) / a$	`g = cos(a*t + b) int(g)` или `int(g, t)`
$\int J_{1} (z) d z = - J_{0} (z)$	`int(besselj(1, z))` или `int(besselj(1, z), z)`

В отличие от дифференциации, символическое интегрирование является более сложной задачей. При вычислении интеграла может возникнуть ряд трудностей:

Антипроизводная, F, может не существовать в закрытой форме.
Антипроизводная может задавать незнакомую функцию.
Антипроизводная может существовать, но программное обеспечение не может найти ее.
Программное обеспечение может найти антипроизводное на большем компьютере, но запусках из времени или памяти на доступной машине.

Тем не менее, во многих случаях MATLAB может успешно выполнить символическое интегрирование. Для примера создайте символьные переменные

syms a b theta x y n u z

Следующая таблица иллюстрирует интегрирование выражений, содержащих эти переменные.

f	int (f)
syms x n f = x^n;	int(f) ans = piecewise(n == -1, log(x), n ~= -1,... x^(n + 1)/(n + 1))
syms y f = y^(-1);	int(f) ans = log(y)
syms x n f = n^x;	int(f) ans = n^x/log(n)
syms a b theta f = sin(a*theta+b);	int(f) ans = -cos(b + a*theta)/a
syms u f = 1/(1+u^2);	int(f) ans = atan(u)
syms x f = exp(-x^2);	int(f) ans = (pi^(1/2)*erf(x))/2

В последнем примере exp(-x^2), не существует формулы для интеграла, включающего стандартные выражения вычисления, такие как тригонометрические и экспоненциальные функции. В этом случае MATLAB возвращает ответ в терминах функции error erf.

Если MATLAB не может найти ответ на интеграл функции f, просто возвращается int(f).

Также возможно определенное интегрирование.

Определенный интеграл	Команда
$\int_{a}^{b} f (x) d x$	`int(f, a, b)`
$\int_{a}^{b} f (v) d v$	`int(f, v, a, b)`

Определенный интеграл

Команда

$\int_{a}^{b} f (x) d x$

int(f, a, b)

$\int_{a}^{b} f (v) d v$

int(f, v, a, b)

Вот несколько дополнительных примеров.

f	a, b	int (f, a, b)
syms x f = x^7;	a = 0; b = 1;	int(f, a, b) ans = 1/8
syms x f = 1/x;	a = 1; b = 2;	int(f, a, b) ans = log(2)
syms x f = log(x)*sqrt(x);	a = 0; b = 1;	int(f, a, b) ans = -4/9
syms x f = exp(-x^2);	a = 0; b = inf;	int(f, a, b) ans = pi^(1/2)/2
syms z f = besselj(1,z)^2;	a = 0; b = 1;	int(f, a, b) ans = hypergeom([3/2, 3/2],... [2, 5/2, 3], -1)/12

Для функции Бесселя (besselj) пример, можно вычислить численное приближение к значению интеграла, используя double функция. Команды

syms z
a = int(besselj(1,z)^2,0,1)

вернуть

a =
hypergeom([3/2, 3/2], [2, 5/2, 3], -1)/12

и команду

a = double(a)

возвраты

a =
    0.0717

Интегрирование с реальными параметрами

Одной из тонкостей, участвующих в символическом интегрировании, является «значение» различных параметров. Для примера, если a является любым положительным вещественным числом, выражение

$e^{- a x^{2}}$

- положительная кривая, имеющая форму колокола, которая имеет тенденцию к 0, поскольку x имеет тенденцию ± ∞. Можно создать пример этой кривой для a = 1/2.

syms x
a = sym(1/2);
f = exp(-a*x^2);
fplot(f)

Figure contains an axes. The axes contains an object of type functionline.

Однако, если вы пытаетесь вычислить интеграл

$\int_{- \infty}^{\infty} e^{- a x^{2}} d x$

не присваивая значение a, MATLAB принимает, что a представляет комплексное число, и поэтому возвращает кусочно-линейный ответ, который зависит от аргумента a. Если вас интересует только случай, когда a является положительным вещественным числом, используйте assume для установки предположения о a:

syms a
assume(a > 0)

Теперь можно вычислить предыдущий интеграл с помощью команд

syms x
f = exp(-a*x^2);
int(f, x, -inf, inf)

Это возвращает

ans =
pi^(1/2)/a^(1/2)

Интегрирование со сложными параметрами

Чтобы вычислить интеграл

$\int_{- \infty}^{\infty} \frac{1}{a^{2} + x^{2}} d x$

для комплексных чисел a, введите

syms a x 
f = 1/(a^2 + x^2);
F = int(f, x, -inf, inf)

Использование syms чтобы удалить все допущения для переменных. Для получения дополнительной информации о символьных переменных и допущениях на них, смотрите Удалить символические объекты и их допущения.

Предыдущие команды генерируют комплексный выход

F = 
(pi*signIm(1i/a))/a

Функция signIm определяется как:

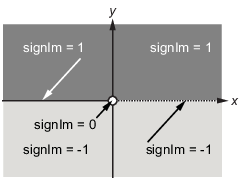
$signIm (z) = {\begin{array}{l} 1 & если Im (z) > 0, или Im (z) = 0 и z < 0 \\ 0 & если z = 0 \\ -1 & иначе . \end{array}$

Чтобы оценить F при a = 1 + i, введите

g = subs(F, 1 + i)

g = 
pi*(1/2 - 1i/2)

double(g)

ans =
   1.5708 - 1.5708i

Высокоточное численное интегрирование с использованием арифметики переменной точности

Высокоточное численное интегрирование реализовано в vpaintegral функция Symbolic Math Toolbox™. vpaintegral использует арифметику переменной точности в отличие от MATLAB integral функция, которая использует арифметику двойной точности.

Интеграция besseli(5,25*u).*exp(-u*25) при помощи обоих integral и vpaintegral. integral функция возвращает NaN и выдает предупреждение vpaintegral возвращает правильный результат.

syms u
f = besseli(5,25*x).*exp(-x*25);
fun = @(u)besseli(5,25*u).*exp(-u*25);

usingIntegral = integral(fun, 0, 30)
usingVpaintegral = vpaintegral(f, 0, 30)

Warning: Infinite or Not-a-Number value encountered. 
usingIntegral =
   NaN

usingVpaintegral =
0.688424

Для получения дополнительной информации см. vpaintegral.

Документация

Интегрирование

Интегрирование с реальными параметрами

Интегрирование со сложными параметрами

Высокоточное численное интегрирование с использованием арифметики переменной точности

Документация Symbolic Math Toolbox

Поддержка