fitlda

Подгонка модели латентного распределения Дирихле (LDA)

Синтаксис

mdl = fitlda(bag,numTopics)

mdl = fitlda(counts,numTopics)

mdl = fitlda(___,Name,Value)

Описание

Модель латентного распределения Дирихле (LDA) является тематической моделью, которая обнаруживает базовые темы в наборе документов и выводит вероятности слов в темах. Если модель подгонялась с помощью модели bag-of-n-gams, то программа рассматривает n-gams как отдельные слова.

пример

mdl = fitlda(bag,numTopics) подходит для модели LDA с numTopics темы для модели мешка слов или мешка n-граммов bag.

пример

mdl = fitlda(counts,numTopics) подходит для модели LDA к документам, представленным матрицей отсчётов частот.

mdl = fitlda(___,Name,Value) задает дополнительные опции, используя один или несколько аргументы пары "имя-значение".

Примеры

свернуть все

Подгонка модели LDA

Открыть Live Script

Чтобы воспроизвести результаты в этом примере, установите rng на 'default'.

rng('default')

Загрузите данные примера. Файл sonnetsPreprocessed.txt содержит предварительно обработанные версии сонетов Шекспира. Файл содержит по одному сонету на линию со словами, разделенными пространством. Извлеките текст из sonnetsPreprocessed.txtразделите текст на документы в символах новой строки, а затем пометьте его токеном.

filename = "sonnetsPreprocessed.txt";
str = extractFileText(filename);
textData = split(str,newline);
documents = tokenizedDocument(textData);

Создайте модель мешка слов с помощью bagOfWords.

bag = bagOfWords(documents)

bag = 
  bagOfWords with properties:

          Counts: [154x3092 double]
      Vocabulary: [1x3092 string]
        NumWords: 3092
    NumDocuments: 154

Подгонка модели LDA с четырьмя темами.

numTopics = 4;
mdl = fitlda(bag,numTopics)

Initial topic assignments sampled in 0.077325 seconds.
=====================================================================================
| Iteration  |  Time per  |  Relative  |  Training  |     Topic     |     Topic     |
|            | iteration  | change in  | perplexity | concentration | concentration |
|            | (seconds)  |   log(L)   |            |               |   iterations  |
=====================================================================================
|          0 |       0.36 |            |  1.215e+03 |         1.000 |             0 |
|          1 |       0.01 | 1.0482e-02 |  1.128e+03 |         1.000 |             0 |
|          2 |       0.01 | 1.7190e-03 |  1.115e+03 |         1.000 |             0 |
|          3 |       0.01 | 4.3796e-04 |  1.118e+03 |         1.000 |             0 |
|          4 |       0.01 | 9.4193e-04 |  1.111e+03 |         1.000 |             0 |
|          5 |       0.01 | 3.7079e-04 |  1.108e+03 |         1.000 |             0 |
|          6 |       0.01 | 9.5777e-05 |  1.107e+03 |         1.000 |             0 |
=====================================================================================

mdl = 
  ldaModel with properties:

                     NumTopics: 4
             WordConcentration: 1
            TopicConcentration: 1
      CorpusTopicProbabilities: [0.2500 0.2500 0.2500 0.2500]
    DocumentTopicProbabilities: [154x4 double]
        TopicWordProbabilities: [3092x4 double]
                    Vocabulary: [1x3092 string]
                    TopicOrder: 'initial-fit-probability'
                       FitInfo: [1x1 struct]

Визуализируйте темы с помощью облаков слов.

figure
for topicIdx = 1:4
    subplot(2,2,topicIdx)
    wordcloud(mdl,topicIdx);
    title("Topic: " + topicIdx)
end

Figure contains objects of type wordcloud. The chart of type wordcloud has title Topic: 1. The chart of type wordcloud has title Topic: 2. The chart of type wordcloud has title Topic: 3. The chart of type wordcloud has title Topic: 4.

Подбор модели LDA к матрице count слов

Открыть Live Script

Подбор модели LDA к набору документов, представленных матрицей count слов.

Чтобы воспроизвести результаты этого примера, установите rng на 'default'.

rng('default')

Загрузите данные примера. sonnetsCounts.mat содержит матрицу отсчётов слов и соответствующий словарь предварительно обработанных версий сонетов Шекспира. Значение counts(i,j) соответствует количеству раз, сколько jВторое слово словаря появляется в iI документ.

load sonnetsCounts.mat
size(counts)

ans = 1×2

         154        3092

Подгонка модели LDA с 7 темами. Чтобы подавить подробный выход, установите 'Verbose' в 0.

numTopics = 7;
mdl = fitlda(counts,numTopics,'Verbose',0);

Визуализация нескольких тематических смесей с помощью сложенных столбчатых диаграмм. Визуализация тематических смесей первых трех входных документов.

topicMixtures = transform(mdl,counts(1:3,:));
figure
barh(topicMixtures,'stacked')
xlim([0 1])
title("Topic Mixtures")
xlabel("Topic Probability")
ylabel("Document")
legend("Topic "+ string(1:numTopics),'Location','northeastoutside')

Figure contains an axes. The axes with title Topic Mixtures contains 7 objects of type bar. These objects represent Topic 1, Topic 2, Topic 3, Topic 4, Topic 5, Topic 6, Topic 7.

Прогнозирование основных тем LDA документов

Открыть Live Script

Чтобы воспроизвести результаты в этом примере, установите rng на 'default'.

rng('default')

filename = "sonnetsPreprocessed.txt";
str = extractFileText(filename);
textData = split(str,newline);
documents = tokenizedDocument(textData);

Создайте модель мешка слов с помощью bagOfWords.

bag = bagOfWords(documents)

bag = 
  bagOfWords with properties:

          Counts: [154x3092 double]
      Vocabulary: [1x3092 string]
        NumWords: 3092
    NumDocuments: 154

Подгонка модели LDA с 20 темами.

numTopics = 20;
mdl = fitlda(bag,numTopics)

Initial topic assignments sampled in 0.029643 seconds.
=====================================================================================
| Iteration  |  Time per  |  Relative  |  Training  |     Topic     |     Topic     |
|            | iteration  | change in  | perplexity | concentration | concentration |
|            | (seconds)  |   log(L)   |            |               |   iterations  |
=====================================================================================
|          0 |       0.39 |            |  1.159e+03 |         5.000 |             0 |
|          1 |       0.13 | 5.4884e-02 |  8.028e+02 |         5.000 |             0 |
|          2 |       0.11 | 4.7400e-03 |  7.778e+02 |         5.000 |             0 |
|          3 |       0.11 | 3.4597e-03 |  7.602e+02 |         5.000 |             0 |
|          4 |       0.14 | 3.4662e-03 |  7.430e+02 |         5.000 |             0 |
|          5 |       0.11 | 2.9259e-03 |  7.288e+02 |         5.000 |             0 |
|          6 |       0.14 | 6.4180e-05 |  7.291e+02 |         5.000 |             0 |
=====================================================================================

mdl = 
  ldaModel with properties:

                     NumTopics: 20
             WordConcentration: 1
            TopicConcentration: 5
      CorpusTopicProbabilities: [1x20 double]
    DocumentTopicProbabilities: [154x20 double]
        TopicWordProbabilities: [3092x20 double]
                    Vocabulary: [1x3092 string]
                    TopicOrder: 'initial-fit-probability'
                       FitInfo: [1x1 struct]

Спрогнозируйте верхние темы для массива новых документов.

newDocuments = tokenizedDocument([
    "what's in a name? a rose by any other name would smell as sweet."
    "if music be the food of love, play on."]);
topicIdx = predict(mdl,newDocuments)

topicIdx = 2×1

    19
     8

Визуализируйте предсказанные темы с помощью облаков слов.

figure
subplot(1,2,1)
wordcloud(mdl,topicIdx(1));
title("Topic " + topicIdx(1))
subplot(1,2,2)
wordcloud(mdl,topicIdx(2));
title("Topic " + topicIdx(2))

Figure contains objects of type wordcloud. The chart of type wordcloud has title Topic 19. The chart of type wordcloud has title Topic 8.

Входные параметры

свернуть все

`bag` - Входная модель
`bagOfWords` | объекта `bagOfNgrams` объект

Входная модель мешка слов или мешка n-граммов, заданная как bagOfWords объект или bagOfNgrams объект. Если bag является bagOfNgrams объект, затем функция обрабатывает каждый n-грамм как одно слово.

`numTopics` - Количество тем
положительное целое число

Количество тем, заданное как положительное целое число. Пример, показывающий, как выбрать количество тем, см. в разделе Выбор количества тем для модели LDA.

Пример: 200

`counts` - Частотные счетчики слов
матрица неотрицательных целых чисел

Счетчики частот слов, заданные как матрица неотрицательных целых чисел. Если вы задаете 'DocumentsIn' чтобы быть 'rows', затем значение counts(i,j) соответствует количеству раз, когда j-е слово словаря появляется во i-м документе. В противном случае значение counts(i,j) соответствует количеству раз, когда i-е слово словаря появляется во j-м документе.

Аргументы в виде пар имя-значение

Задайте необязательные разделенные разделенными запятой парами Name,Value аргументы. Name - имя аргумента и Value - соответствующее значение. Name должны находиться внутри кавычек. Можно задать несколько аргументов в виде пар имен и значений в любом порядке Name1,Value1,...,NameN,ValueN.

Пример: 'Solver','avb' задает, чтобы использовать в качестве решателя приблизительные вариационные Байеса.

Опции решателя

свернуть все

`'Solver'` - Решатель для оптимизации
`'cgs'` (по умолчанию) | `'savb'` | `'avb'` | `'cvb0'`

Решатель для оптимизации, заданный как разделенная разделенными запятой парами, состоящая из 'Solver' и одно из следующих:

Решатель Стохастика

'savb' - Используйте стохастическую аппроксимацию вариационного Байеса [1] . Этот решатель лучше всего подходит для больших [2]наборов данных и может подгонять хорошую модель за меньшее количество проходов данных.

Пакетные решатели

'cgs' - Использование свернутой выборки Гиббса [3]. Этот решатель может быть более точным за счет более длительного запуска. resume функция не поддерживает модели, оснащенные CGS.
'avb' - Используйте приблизительные вариационные Байеса [4]. Этот решатель обычно запускается быстрее, чем свернутая выборка Гиббса и свернутая вариационная Байеса, но может быть менее точным.
'cvb0' - Используйте свернутые вариационные Байеса, нули порядка [4] . Этот решатель может быть более точным, чем [5]приблизительный вариационный Бейес, за счет более длительного запуска.

Пример, показывающий сравнение решателей, см. в разделе Сравнение решателей LDA.

Пример: 'Solver','savb'

`'LogLikelihoodTolerance'` - Относительная погрешность по логарифмической правдоподобности
`0.0001` (по умолчанию) | положительная скалярная величина

Относительная погрешность по логарифмической правдоподобности, заданный как разделенная разделенными запятой парами, состоящая из 'LogLikelihoodTolerance' и положительная скалярная величина. Оптимизация заканчивается, когда достигается этот допуск.

Пример: 'LogLikelihoodTolerance',0.001

`'FitTopicProbabilities'` - Опция для подбора тематических вероятностей корпуса
`true` (по умолчанию) | `false`

Опция для подгонки концентрации темы, заданная как разделенная разделенными запятой парами, состоящая из 'FitTopicConcentration' и любой из них true или false.

Функция подходит для Dirichlet private $α = α_{0} (\begin{matrix} p_{1} & p_{2} & \dots & p_{K} \end{matrix})$ по теме смеси, где $α_{0}$ является темой концентрации и $p_{1}, \dots, p_{K}$ являются вероятностями corpus topic, которые равны 1.

Пример: 'FitTopicProbabilities',false

Типы данных: logical

`'FitTopicConcentration'` - Опция для подгонки тематической концентрации
`true` | `false`

Для пакета решатели 'cgs', 'avb', и 'cvb0', по умолчанию для FitTopicConcentration является true. Для стохастического решателя 'savb', по умолчанию является false.

Пример: 'FitTopicConcentration',false

Типы данных: logical

`'InitialTopicConcentration'` - Первоначальная оценка концентрации темы
`numTopics/4` (по умолчанию) | неотрицательной скаляром

Начальная оценка концентрации темы, заданная как разделенная разделенными запятой парами, состоящая из 'InitialTopicConcentration' и неотрицательный скаляр. Функция устанавливает концентрацию по темам равной TopicConcentration/NumTopics. Для получения дополнительной информации смотрите Латентное распределение Дирихле.

Пример: 'InitialTopicConcentration',25

`'TopicOrder'` - Порядок топик
`'initial-fit-probability'` (по умолчанию) | `'unordered'`

Порядок темы, заданный как один из следующих:

'initial-fit-probability' - Сортировка тем по вероятностям corpus topic входа набора документов (CorpusTopicProbabilities свойство).
'unordered' - Не сортировать темы.

`'WordConcentration'` - Концентрация слов
`1` (по умолчанию) | неотрицательной скаляром

Концентрация слова, заданная как разделенная разделенными запятой парами, состоящая из 'WordConcentration' и неотрицательный скаляр. Программное обеспечение устанавливает Dirichlet previous по темам (слово вероятностей по темам) как симметричный параметр распределения Dirichlet со значением WordConcentration/numWords, где numWords - размер словаря входных документов. Для получения дополнительной информации смотрите Латентное распределение Дирихле.

`'DocumentsIn'` - Ориентация документов
`'rows'` (по умолчанию) | `'columns'`

Ориентация документов в матрице count слов, заданная как разделенная разделенными запятой парами, состоящая из 'DocumentsIn' и одно из следующих:

'rows' - Вход является матрицей счетчиков слов со строками, соответствующими документам.
'columns' - Вход является транспонированной матрицей счетчиков слов со столбцами, соответствующими документам.

Эта опция применяется только в том случае, если документы входа заданы как матрица счетчиков слов.

Примечание

Если вы ориентируете матрицу count слов так, чтобы документы соответствовали столбцам и задавали 'DocumentsIn','columns', тогда вы можете испытать значительное сокращение времени оптимизации-выполнения.

Опции решателя пакета

свернуть все

`'IterationLimit'` - Максимальное количество итераций
`100` (по умолчанию) | положительное целое число

Максимальное количество итераций, заданное как разделенная разделенными запятой парами, состоящая из 'IterationLimit' и положительное целое число.

Эта опция поддерживает только пакетные решатели ('cgs', 'avb', или 'cvb0').

Пример: 'IterationLimit',200

Опции Стохастического решателя

свернуть все

`'DataPassLimit'` - Максимальное количество проходов через данные
1 (по умолчанию) | положительное целое число

Максимальное количество проходов через данные, заданное как разделенная разделенными запятой парами, состоящая из 'DataPassLimit' и положительное целое число.

Если вы задаете 'DataPassLimit' но не 'MiniBatchLimit', затем значение по умолчанию 'MiniBatchLimit' игнорируется. Если вы задаете оба 'DataPassLimit' и 'MiniBatchLimit', затем fitlda использует аргумент, который приводит к обработке наименьшего количества наблюдений.

Эта опция поддерживает только стохастическую ('savb') решатель.

Пример: 'DataPassLimit',2

`'MiniBatchLimit'` - Максимальное количество проходов мини-партии
положительное целое число

Максимальное количество проходов мини-пакета, заданное как разделенная разделенными запятой парами, состоящая из 'MiniBatchLimit' и положительное целое число.

Если вы задаете 'MiniBatchLimit' но не 'DataPassLimit', затем fitlda игнорирует значение по умолчанию 'DataPassLimit'. Если вы задаете оба 'MiniBatchLimit' и 'DataPassLimit', затем fitlda использует аргумент, который приводит к обработке наименьшего количества наблюдений. Значение по умолчанию ceil(numDocuments/MiniBatchSize), где numDocuments количество входа документов.

Эта опция поддерживает только стохастическую ('savb') решатель.

Пример: 'MiniBatchLimit',200

`'MiniBatchSize'` - Размер мини-партии
1000 (по умолчанию) | положительное целое число

Мини-пакет, заданный как разделенная разделенными запятой парами, состоящая из 'MiniBatchLimit' и положительное целое число. Функция обрабатывает MiniBatchSize документы в каждой итерации.

Эта опция поддерживает только стохастическую ('savb') решатель.

Пример: 'MiniBatchSize',512

`'LearnRateDecay'` - Падение скорости обучения
0,5 (по умолчанию) | положительная скалярная величина, меньше или равный 1

Падение скорости обучения, заданное как разделенная разделенными запятой парами 'LearnRateDecay' и a положительной скалярной величины меньше или равной 1.

Для мини-пакетных t функция устанавливает скорость обучения равной $η (t) = 1 / {(1 + t)}^{κ}$ , где $κ$ - падение скорости обучения.

Если LearnRateDecay близок к 1, затем скорость обучения падает быстрее, и модель учится в основном из более ранних мини-пакетов. Если LearnRateDecay близок к 0, затем скорость обучения замедляется, и модель продолжает учиться из большего количества мини-пакетов. Для получения дополнительной информации см. «Стохастический решатель».

Эта опция поддерживает только стохастический решатель ('savb').

Пример: 'LearnRateDecay',0.75

Параметры отображения

свернуть все

`'ValidationData'` - Данные валидации
`[]` (по умолчанию) | `bagOfWords` | объекта `bagOfNgrams` объект | разреженной матрицей счетчиков слов

Данные валидации для мониторинга сходимости оптимизации, заданные как разделенная разделенными запятой парами, состоящая из 'ValidationData' и a bagOfWords объект, a bagOfNgrams объект или разреженная матрица отсчётов слов. Если данные валидации являются матрицей, то данные должны иметь ту же ориентацию и то же количество слов, что и входные документы.

`'ValidationFrequency'` - Частота валидации модели
положительное целое число

Частота валидации модели в количестве итераций, заданная как разделенная разделенными запятой парами, состоящая из 'ValidationFrequency' и положительное целое число.

Значение по умолчанию зависит от решателя, используемого для подгонки модели. Для стохастического решателя значение по умолчанию является 10. Для других решателей значение по умолчанию является 1.

`'Verbose'` - Уровень подробностей
1 (по умолчанию) | 0

Уровень подробностей, заданный как разделенная разделенными запятой парами, состоящая из 'Verbose' и одно из следующих:

0 - Не отображать подробные выходы.
1 - отображение информации о прогрессе.

Пример: 'Verbose',0

Выходные аргументы

свернуть все

`mdl` - Выходная модель LDA
`ldaModel` объект

Выход модели LDA, возвращенной как ldaModel объект.

Подробнее о

свернуть все

Латентное распределение дирихле

Модель латентного распределения Дирихле (LDA) является моделью темы документа, которая обнаруживает базовые темы в наборе документов и выводит вероятности слов в темах. LDA моделирует набор D документов как тематические смеси $θ_{1}, \dots, θ_{D}$ , над K темами, характеризующимися векторами вероятностей слова $φ_{1}, \dots, φ_{K}$ . Модель принимает, что тематические смеси $θ_{1}, \dots, θ_{D}$ , и темы $φ_{1}, \dots, φ_{K}$ следуйте распределению Дирихле с параметрами концентрации $α$ и $β$ соответственно.

Тематические смеси $θ_{1}, \dots, θ_{D}$ являются векторами вероятностей длины K, где K - количество тем. Вход $θ_{d i}$ - вероятность появления i темы в d-м документе. Тематические смеси соответствуют строкам DocumentTopicProbabilities свойство ldaModel объект.

Темы $φ_{1}, \dots, φ_{K}$ являются векторами вероятностей длины V, где V - количество слов в словаре. Вход $φ_{i v}$ соответствует вероятности появления v-го слова словаря в i-й теме. Темы $φ_{1}, \dots, φ_{K}$ соответствуют столбцам TopicWordProbabilities свойство ldaModel объект.

Учитывая темы $φ_{1}, \dots, φ_{K}$ и Дирихлет априорный $α$ что касается тематических смесей, то LDA предполагает следующий генеративный процесс для документа:

Образец тематической смеси $θ ~ Dirichlet (α)$ . Случайная переменная $θ$ является вектором вероятностей длины K, где K - количество тем.
Для каждого слова в документе:
1. Пример индекса темы $z ~ Categorical (θ)$ . z случайной переменной является целым числом от 1 до K, где K - количество тем.
2. Пример слова $w ~ Categorical (φ_{z})$ . Случайная переменная w является целым числом от 1 до V, где V - количество слов в словаре, и представляет соответствующее слово в словаре.

В рамках этого генеративного процесса совместное распределение документа со словами $w_{1}, \dots, w_{N}$ , с тематической смесью $θ$ , и с индексами тем $z_{1}, \dots, z_{N}$ дается

$p (θ, z, w | α, φ) = p (θ | α) \prod_{n = 1}^{N} p (z_{n} | θ) p (w_{n} | z_{n}, φ),$

где N - количество слов в документе. Суммирование распределения соединений по z и последующая интеграция $θ$ приводит к маргинальному распределению документа w:

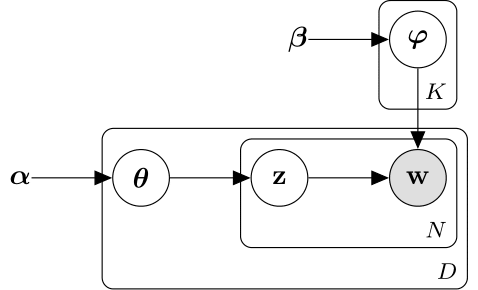
$p (w | α, φ) = \int_{θ} p (θ | α) \prod_{n = 1}^{N} \sum_{z_{n}} p (z_{n} | θ) p (w_{n} | z_{n}, φ) d θ .$

Следующая схема иллюстрирует модель LDA как вероятностную графическую модель. Затененные узлы являются наблюдаемыми переменными, незаштрихованные узлы являются скрытыми переменными, узлы без контуров являются параметрами модели. Стрелы подсвечивают зависимости между случайными переменными, а пластины указывают на повторные узлы.

Распределение Дирихле

Распределение Дирихле является непрерывным обобщением полиномиального распределения. Учитывая количество категорий $K \geq 2$ , и параметр концентрации $α$ , где $α$ является вектором положительных реалов длины K, функция плотности вероятностей распределения Дирихле задается как

$p (θ ∣ α) = \frac{1}{B (α)} \prod_{i = 1}^{K} θ_{i}^{α_{i} - 1},$

где B обозначает многомерную бета-функцию, заданную как

$B (α) = \frac{\prod_{i = 1}^{K} Γ (α_{i})}{Γ (\sum_{i = 1}^{K} α_{i})} .$

Частным случаем распределения Дирихле является симметричное распределение Дирихле. Симметричное распределение Дирихле характеризуется параметром концентрации $α$ , где все элементы $α$ те же самые.

Решатель Стохастика

Стохастический решатель обрабатывает документы мини-пакетами. Он обновляет вероятности слова по теме с помощью взвешенной суммы вероятностей, вычисленных из каждого мини-пакета, и вероятностей из всех предыдущих мини-пакетов.

Для мини-пакетных t решатель устанавливает скорость обучения на $η (t) = 1 / {(1 + t)}^{κ}$ , где $κ$ - падение скорости обучения.

Функция использует падение скорости обучения, чтобы обновить $Φ$ , матрица вероятностей слов по темам, путем установки

$Φ^{(t)} = (1 - η (t)) Φ^{(t - 1)} + η (t) Φ^{(t *)},$

где $Φ^{(t *)}$ - матрица, полученная из мини-пакетных t, и $Φ^{(t - 1)}$ - матрица, полученная из мини-пакетов с 1 по t -1 .

Перед началом обучения (когда t = 0) функция инициализирует начальные вероятности слова по теме $Φ^{(0)}$ со случайными значениями.

Вопросы совместимости

расширить все

`fitlda` сортирует темы

Поведение изменено в R2018b

Начиная с R2018b, fitldaпо умолчанию сортирует темы в порядке убывания вероятностей тем набора входных документов. Это поведение облегчает поиск тем с наивысшими вероятностями.

В предыдущих версиях, fitlda не изменяет порядок топик. Чтобы воспроизвести поведение, установите 'TopicOrder' опция для 'unordered'.

Ссылки

[1] Фолдс, Джеймс, Леви Бойлз, Кристофер Дюбуа, Падраик Смит и Max Веллинг. Стохастический свернутый вариационный байесовский вывод для латентного распределения Дирихле. В Трудах 19-й международной конференции ACM SIGKDD по открытию знаний и майнингу данных, стр. 446-454. ACM, 2013.

[2] Хоффман, Мэтью Д., Дэвид М. Блей, Чонг Ван и Джон Пейсли. «Стохастический вариационный вывод». The Journal of Машинное Обучение Research 14, № 1 (2013): 1303-1347.

[3] Гриффитс, Томас Л. и Марк Стейверс. «Поиск научных тем». Труды Национальной академии наук 101, нет. суппл 1 (2004): 5228-5235.

[4] Asuncion, Arthur, Max Welling, Padhraic Smyth, and Yee Whye Teh. «О сглаживании и выводе для тематических моделей». В трудах двадцать пятой Конференции по неопределенности в искусственном интеллекте, стр. 27-34. AUAI Press, 2009.

[5] Teh, Yee W., David Newman, and Max Welling. «Свернутый вариационный алгоритм вывода Байеса для латентного распределения Дирихле». В «Усовершенствования в системах нейронной обработки информации», стр. 1353-1360. 2007.

См. также

Темы

Введенный в R2017b

Документация

fitlda

Синтаксис

Описание

Примеры

Подгонка модели LDA

Подбор модели LDA к матрице count слов

Прогнозирование основных тем LDA документов

Входные параметры

bag - Входная модель bagOfWords | объекта bagOfNgrams объект

numTopics - Количество тем положительное целое число

counts - Частотные счетчики слов матрица неотрицательных целых чисел

Аргументы в виде пар имя-значение

'Solver' - Решатель для оптимизации 'cgs' (по умолчанию) | 'savb' | 'avb' | 'cvb0'

'LogLikelihoodTolerance' - Относительная погрешность по логарифмической правдоподобности 0.0001 (по умолчанию) | положительная скалярная величина

'FitTopicProbabilities' - Опция для подбора тематических вероятностей корпуса true (по умолчанию) | false

'FitTopicConcentration' - Опция для подгонки тематической концентрации true | false

'InitialTopicConcentration' - Первоначальная оценка концентрации темы numTopics/4 (по умолчанию) | неотрицательной скаляром

'TopicOrder' - Порядок топик 'initial-fit-probability' (по умолчанию) | 'unordered'

'WordConcentration' - Концентрация слов 1 (по умолчанию) | неотрицательной скаляром

'DocumentsIn' - Ориентация документов 'rows' (по умолчанию) | 'columns'

'IterationLimit' - Максимальное количество итераций 100 (по умолчанию) | положительное целое число

'DataPassLimit' - Максимальное количество проходов через данные 1 (по умолчанию) | положительное целое число

'MiniBatchLimit' - Максимальное количество проходов мини-партии положительное целое число

'MiniBatchSize' - Размер мини-партии 1000 (по умолчанию) | положительное целое число

'LearnRateDecay' - Падение скорости обучения 0,5 (по умолчанию) | положительная скалярная величина, меньше или равный 1

'ValidationData' - Данные валидации [] (по умолчанию) | bagOfWords | объекта bagOfNgrams объект | разреженной матрицей счетчиков слов

'ValidationFrequency' - Частота валидации модели положительное целое число

'Verbose' - Уровень подробностей 1 (по умолчанию) | 0

Выходные аргументы

mdl - Выходная модель LDA ldaModel объект

Подробнее о

Латентное распределение дирихле

Распределение Дирихле

Решатель Стохастика

Вопросы совместимости

fitlda сортирует темы

Ссылки

См. также

Темы

Symbolic Math Toolbox

Поддержка

`bag` - Входная модель
`bagOfWords` | объекта `bagOfNgrams` объект

`numTopics` - Количество тем
положительное целое число

`counts` - Частотные счетчики слов
матрица неотрицательных целых чисел

`'Solver'` - Решатель для оптимизации
`'cgs'` (по умолчанию) | `'savb'` | `'avb'` | `'cvb0'`

`'LogLikelihoodTolerance'` - Относительная погрешность по логарифмической правдоподобности
`0.0001` (по умолчанию) | положительная скалярная величина

`'FitTopicProbabilities'` - Опция для подбора тематических вероятностей корпуса
`true` (по умолчанию) | `false`

`'FitTopicConcentration'` - Опция для подгонки тематической концентрации
`true` | `false`

`'InitialTopicConcentration'` - Первоначальная оценка концентрации темы
`numTopics/4` (по умолчанию) | неотрицательной скаляром

`'TopicOrder'` - Порядок топик
`'initial-fit-probability'` (по умолчанию) | `'unordered'`

`'WordConcentration'` - Концентрация слов
`1` (по умолчанию) | неотрицательной скаляром

`'DocumentsIn'` - Ориентация документов
`'rows'` (по умолчанию) | `'columns'`

`'IterationLimit'` - Максимальное количество итераций
`100` (по умолчанию) | положительное целое число

`'DataPassLimit'` - Максимальное количество проходов через данные
1 (по умолчанию) | положительное целое число

`'MiniBatchLimit'` - Максимальное количество проходов мини-партии
положительное целое число

`'MiniBatchSize'` - Размер мини-партии
1000 (по умолчанию) | положительное целое число

`'LearnRateDecay'` - Падение скорости обучения
0,5 (по умолчанию) | положительная скалярная величина, меньше или равный 1

`'ValidationData'` - Данные валидации
`[]` (по умолчанию) | `bagOfWords` | объекта `bagOfNgrams` объект | разреженной матрицей счетчиков слов

`'ValidationFrequency'` - Частота валидации модели
положительное целое число

`'Verbose'` - Уровень подробностей
1 (по умолчанию) | 0

`mdl` - Выходная модель LDA
`ldaModel` объект

`fitlda` сортирует темы