Longitudinal Wheel

Продольное колесо с диском, барабаном или картографическим тормозом

Библиотека:
Силовой агрегат Blockset/Drivetrain/Колеса
Динамика автомобиля Blockset/Колеса и шины

Описание

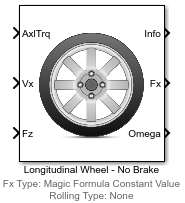
Блок Longitudinal Wheel реализует продольное поведение идеального колеса. Можно задать метод вычисления продольной силы и сопротивления качению и тип тормоза. Используйте блок в симуляциях привода и продольных транспортных средств, где для определения ускорения, торможения и сопротивления качению колес требуются низкочастотные шина-дорога и тормозные силы. Например, можно использовать блок, чтобы определить крутящий момент и требования к степени для заданного цикла привода или события торможения. Блок не подходит для приложений, которые требуют комбинированного бокового скольжения.

Существует четыре типа блоков Longitudinal Wheel. Каждый блок реализует свой тип тормоза.

Имя блока	Настройка типа тормоза	Реализация тормозов
Longitudinal Wheel - No Brake	`None`	Ничего
Longitudinal Wheel - Disc Brake	`Disc`	Тормоз, который преобразует давление в тормозном цилиндре в тормозное усилие.
Longitudinal Wheel - Drum Brake	`Drum`	Барабанный тормоз Simplex, который преобразует приложенную силу и геометрию тормоза в сетевой тормозной крутящий момент.
Longitudinal Wheel - Mapped Brake	`Mapped`	Интерполяционная таблица, которая является функцией скорости и прикладываемого тормозного давления колеса.

Блок моделирует продольную силу как функцию скольжения колеса относительно поверхности дороги. Чтобы вычислить продольную силу, задайте один из следующих Longitudinal Force параметров.

Настройка	Реализация блока
`Magic Formula constant value`	Магическая формула с постоянным коэффициентом жесткости, формы, пика и кривизны.
`Magic Formula pure longitudinal slip`	Магическая формула с зависимыми от нагрузки коэффициентами, которые реализуют уравнения 4.E9 через 4.E18 в Шине и Динамике аппарата.
`Mapped force`	Интерполяционная таблица, которая является функцией нормальной силы и коэффициента скольжения колеса.

Чтобы вычислить крутящий момент сопротивления качению, задайте один из следующих Rolling Resistance параметров.

Настройка	Реализация блока
`None`	Ничего
`Pressure and velocity`	Метод в методике ступенчатого прибрежного бурения для измерения сопротивления качению шин. Сопротивление качению является функцией давления в шине, нормальной силы и скорости.
`ISO 28580`	Метод, указанный в ISO 28580:2018, Метод измерения сопротивления качению легковых, грузовых и автобусных шин - Однофазная точка тест и корреляция результатов измерений.
`Magic Formula`	Магические формульные уравнения из 4.E70 в Tire и Динамику аппарата. Магическая формула является эмпирическим уравнением, основанным на аппроксимационных коэффициентах.
`Mapped torque`	Интерполяционная таблица, которая является функцией от нормальной силы и продольной скорости оси спина.

Чтобы вычислить вертикальное движение, задайте один из следующих Vertical Motion параметров.

Настройка	Реализация блока
`None`	Блок передает приложенные силы шасси непосредственно к вычислениям сопротивления качению и продольной силы.
`Mapped stiffness and damping`	Вертикальное движение зависит от жесткости колеса и демпфирования. Жесткость является функцией перемещения боковой стенки шины и давления. Демпфирование является функцией скорости и давления боковой стенки шины.

Динамика Вращательного Колеса

Блок вычисляет инерционную характеристику колеса, удовлетворяющего:

Потери на оси
Тормозной и приводной крутящий момент
Сопротивление качению шин
Контакт заземления через интерфейс шина-дорога

Входной крутящий момент является суммированием приложенного крутящего момента оси, тормозного момента и момента, возникающего из-за объединенного крутящего момента шины.

$T_{i} = T_{a} - T_{b} + T_{d}$

На момент, вытекающий из комбинированного крутящего момента шины, блок реализует силы тягового колеса и сопротивление качению с динамикой первого порядка. Сопротивление качению имеет постоянную по времени, параметризованную с точки зрения длины релаксации.

$T_{d} (s) = \frac{1}{\frac{| ω | R_{e}}{L_{e}} s + 1} (F_{x} R_{e} + M_{y})$

Чтобы вычислить крутящий момент сопротивления качению, можно задать один из следующих Rolling Resistance параметров.

Настройка	Реализация блока
`None`	Блок устанавливает сопротивление качению, `_My`, в нуль.
`Pressure and velocity`	Блок использует метод в SAE Stepwise Coastdown Methodology для измерения сопротивления качению шин. Сопротивление качению является функцией давления в шине, нормальной силы и скорости. В частности, $M_{y} = R_{e} {a + b \| V_{x} \| + c V_{x}^{2}} {F_{z}^{β} p_{i}^{α}} \tanh (4 V_{x})$
`ISO 28580`	Блок использует метод, указанный в ISO 28580:2018, Метод измерения сопротивления качению легкового автомобиля, грузового автомобиля и автобуса - Однофазная точка тест и корреляция результатов измерений. Метод учитывает нормальную нагрузку, паразитарные потери и тепловые коррекции от условий тестирования. В частности, $M_{y} = R_{e} (\frac{F_{z} C_{r}}{1 + K_{t} (T_{a m b} - T_{m e a s})} - F_{p l}) \tanh (ω)$
`Magic Formula`	Блок вычисляет сопротивление качению, `_My`, используя уравнения Магической Формулы из 4.E70 в Шине и Динамике аппарата. Магическая формула является эмпирическим уравнением, основанным на аппроксимационных коэффициентах.
`Mapped torque`	Для сопротивления качению, `_My`, блок использует интерполяционную таблицу, которая является функцией от нормальной силы и продольной скорости оси вращения.

Если тормоза включены, блок определяет условие блокировки или разблокировки торможения на основе идеализированной модели трения сухой муфты. На основе условия блокировки блок реализует эти модели трения и динамики.

Если	Блокировка Условия	Модель трения	Динамическая модель
$\begin{array}{l} ω \neq 0 \\ или \\ T_{S} < \| T_{i} + T_{f} - ω b \| \end{array}$	Незапертый	$\begin{array}{l} T_{f} = T_{k} \\ где, \\ T_{k} = F_{c} R_{e f f} μ_{k} \tanh [4 (- ω_{d})] \\ T_{s} = F_{c} R_{e f f} μ_{s} \\ R_{e f f} = \frac{2 (R_{o}^{3} - R_{i}^{3})}{3 (R_{o}^{2} - R_{i}^{2})} \end{array}$	$\dot{ω} J = - ω b + T_{i} + T_{o}$
$\begin{array}{l} ω = 0 \\ и \\ T_{S} \geq \| T_{i} + T_{f} - ω b \| \end{array}$	Запертый	$T_{f} = T_{s}$	$ω = 0$

В уравнениях используются эти переменные.

ω	Скорость вращения колеса
a	Независимая от скорости силовой компонент
b	Компонент линейной силы скорости
c	Квадратичная сила скорости компонента
_Le	Длина релаксации шин
J	Момент инерции
_My	Крутящий момент сопротивления качению
_Ta	Приложенный крутящий момент на оси
_Tb	Тормозной крутящий момент
_Td	Комбинированный крутящий момент в шинах
_Tf	Фрикционный крутящий момент
_Ti	Крутящий момент входа сети
_Tk	Кинетический фрикционный крутящий момент
_To	Крутящий момент выхода сети
_Ts	Статический крутящий момент трения
_Fc	Приложенная сила сцепления
_Fx	Продольная сила, развиваемая интерфейсом дороги шины из-за скольжения
_Reff	Эффективный радиус сцепления
_Ro	Внешний радиус кольцевого диска
_Ri	Внутренний радиус кольцевого диска
_Re	Эффективный радиус шины при нагрузке и при заданном давлении
_Vx	Скорость продольной оси
_Fz	Нормальная сила транспортного средства
_Cr	Постоянное сопротивление качению
_Tamb	Температура окружающей среды
_Tmeas	Измеренная температура для постоянного сопротивления качению
_Fpl	Потеря паразитной силы
_Kt	Коэффициент тепловой коррекции
ɑ	Экспонента давления в шинах
β	Нормальная экспонента силы
_pi	Давление в шинах
_μs	Коэффициент статического трения
_μk	Коэффициент кинетического трения

Тормоза

Диск

Если вы задаете параметр Brake Type Discблок реализует дисковый тормоз. Этот рисунок показывает вид сбоку и спереди дискового тормоза.

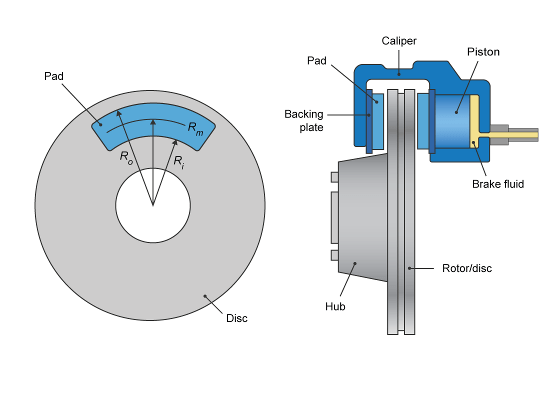
Front and side view of disc brake, showing pad, disc, and caliper

Дисковый тормоз преобразует давление в тормозном цилиндре из тормозного цилиндра в усилие. Дисковый тормоз прикладывает силу к среднему радиусу тормозной колодки.

Блок использует эти уравнения, чтобы вычислить момент привода для дискового тормоза.

$T = {\begin{matrix} \frac{μ P π B_{a}^{2} R_{m} N_{p a d s}}{4} когда N \neq 0 \\ \frac{μ_{s t a t i c} P π B_{a}^{2} R_{m} N_{p a d s}}{4} когда N = 0 \end{matrix}$

$R m = \frac{R o + R i}{2}$

В уравнениях используются эти переменные.

T	Момент привода
P	Прикладываемое тормозное давление
N	Скорость колеса
_Npads	Количество тормозных колодок в узле дискового тормоза
_μstatic	Коэффициент статического трения пары диск-колодка
μ	Коэффициент кинетического трения пары диск-колодка
_Ba	Внутренний диаметр тормозного цилиндра суппорта
_Rm	Средний радиус приложения силы тормозной колодки на роторе тормоза
_Ro	Внешний радиус тормозной колодки
_Ri	Внутренний радиус тормозной колодки

Барабан

Если вы задаете параметр Brake Type Drum, блок реализует статический (статический) симплексный барабанный тормоз. Симплексный барабанный тормоз состоит из одного двустороннего гидравлического привода и двух тормозных колодок. Тормозные колодки не имеют общего шарнирного контакта.

Модель симплексного барабанного тормоза использует приложенную силу и геометрию тормоза, чтобы вычислить крутящий момент привода для каждой тормозной колодки. Модель барабана принимает, что приводы и геометрия башмака симметричны для обеих сторон, позволяя использовать один набор геометрии и параметров трения для обеих башмаков.

Блок реализует уравнения, которые получают из этих уравнений в Основах Элементов Машины.

$\begin{array}{l} T_{r s h o e} = (\frac{π μ c r (\cos θ_{2} - \cos θ_{1}) B_{a}^{2}}{2 μ (2 r (\cos θ_{2} - \cos θ_{1}) + a (\cos^{2} θ_{2} - \cos^{2} θ_{1})) + a r (2 θ_{1} - 2 θ_{2} + \sin 2 θ_{2} - \sin 2 θ_{1})}) P \\ T_{l s h o e} = (\frac{π μ c r (\cos θ_{2} - \cos θ_{1}) B_{a}^{2}}{- 2 μ (2 r (\cos θ_{2} - \cos θ_{1}) + a (\cos^{2} θ_{2} - \cos^{2} θ_{1})) + a r (2 θ_{1} - 2 θ_{2} + \sin 2 θ_{2} - \sin 2 θ_{1})}) P \end{array}$

$T = {\begin{matrix} T_{r s h o e} + T_{l s h o e} when N \neq 0 \\ (T_{r s h o e} + T_{l s h o e}) \frac{μ_{s t a t i c}}{μ} когда N = 0 \end{matrix}$

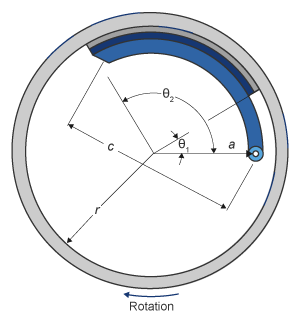
Side view of drum brake

В уравнениях используются эти переменные.

T	Момент привода
P	Прикладываемое тормозное давление
N	Скорость колеса
_μstatic	Коэффициент статического трения пары диск-колодка
μ	Коэффициент кинетического трения пары диск-колодка
_Trshoe	Момент привода правой колодки
_Tlshoe	Момент привода левой колодки
a	Расстояние от центра барабана до шарнира контакта центра башмака
c	Расстояние от шарнира контакта центра колодки до соединения привода тормоза на колодке тормоза
r	Внутренний радиус барабана
_Ba	Внутренний диаметр тормозного цилиндра суппорта
_Θ1	Угол от шарнира контакта центра колодки до начала материала тормозной колодки на колодке
_Θ2	Угол от шарнира контакта центра к концу материала тормозной колодки на колодке

Нанесенный на карту

Если вы задаете параметр Brake Type Mappedблок использует интерполяционную таблицу, чтобы определить момент привода.

$T = {\begin{matrix} f_{b r a k e} (P, N) when N \neq 0 \\ (\frac{μ_{s t a t i c}}{μ}) f_{b r a k e} (P, N) когда N = 0 \end{matrix}$

В уравнениях используются эти переменные.

T	Момент привода
$f_{b r a k e}^{} (P, N)$	Интерполяционная таблица момента привода
P	Прикладываемое тормозное давление
N	Скорость колеса
_μstatic	Коэффициент трения интерфейса «поверхность-поверхность барабана» при статических условиях
μ	Коэффициент трения интерфейса диск-ротор

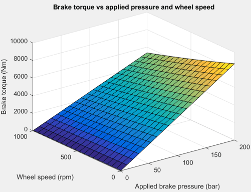
Интерполяционная таблица для крутящего момента привода, $f_{b r a k e}^{} (P, N)$ , является функцией прикладываемого тормозного давления и скорости вращения колеса, где:

T - момент привода, в Н· м.
P прикладываемого тормозного давления, в баре.
N - скорость колеса, в об/мин.

Plot of brake torque as a function of wheel speed and applied brake pressure

Продольная Сила

Чтобы смоделировать Longitudinal Wheel блок продольных сил, можно использовать Формулу Магии. Модель обеспечивает установившийся <reservedrangesplaceholder5> <reservedrangesplaceholder4> x = f (κ, <reservedrangesplaceholder1> z), продольный <reservedrangesplaceholder0> x силы на шине, на основе:

Вертикальная нагрузка F z
Скольжение по κ

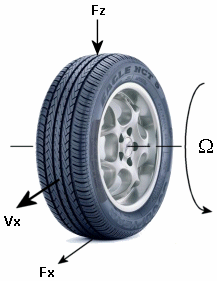
Image of tire with applied vertical and longitudinal forces

Модель Магической Формулы использует эти переменные.

Ω	Скорость вращения колеса
r w	Радиус колеса
V x	Продольная скорость ступицы колеса
_rwΩ	Продольная скорость протектора шины
V _sx = _r w, - V x	Скорость скольжения колеса
κ = V _sx/\| V x \|	Проскальзывание колеса
F z, _F z0	Вертикальная нагрузка и номинальная вертикальная нагрузка на шину
F x = f (κ, F z)	Продольная сила, действующая на шину в точке контакта. Также характерная функция f шины.

Магия Формулы Константа Значение

Если вы задаете Longitudinal Force Magic Formula constant valueблок реализует Формулу Магии как определенную форму функции характеристики шины, характеризующуюся четырехмерными коэффициентами (B, C, D, E) или жесткостью, формой, пиком и кривизной:

$F_{x} = f (κ, F_{z}) = F_{z} D sin (C \tan^{- 1} [{B κ - E [B κ - \tan^{- 1} (B κ)]}])$

Наклон f в κ = 0 является <reservedrangesplaceholder3> <reservedrangesplaceholder2> <reservedrangesplaceholder1> · <reservedrangesplaceholder0> z.

Коэффициенты основаны на эмпирических данных о шинах. Эти значения являются типичными наборами постоянных коэффициентов Magic Formula для общих дорожных условий.

Поверхность	B	C	D	E
Сухой тармак	10	1.9	1	0.97
Мокрый тармак	12	2.3	0.82	1
Снег	5	2	0.3	1
Лед	4	2	0.1	1

Магия Формула Чистый Продольный Скольжение

Если вы задаете Longitudinal Force Magic Formula pure longitudinal slip, блок реализует более общую Формулу Магии, используя безразмерные коэффициенты, которые являются функциями нагрузки шины. Блок реализует уравнения продольной силы в главе 4 Шины и Динамика аппарата, включая 4.E9 через 4.E18:

$\begin{array}{l} F_{x 0} = D_{x} sin (C_{x} \tan^{- 1} [{B_{x} κ_{x} - E_{x} [B_{x} κ_{x} - \tan^{- 1} (B_{x} κ_{x})]}]) + S_{Vx} \\ где: \\ κ_{x} = κ + S_{H x} \\ C_{x} = p_{C x 1} λ_{C x} \\ D_{x} = μ_{x} F_{z} ς_{1} \\ μ_{x} = (p_{D x 1} + p_{D x 2} d f_{z}) (1 + p_{p x 3} d p_{i} + p_{p x 4} d p_{i}^{2}) (1 - p_{D x 3} γ^{2}) λ^{*}_{μ x} \\ E_{x} = (p_{E x 1} + p_{E x 2} d f_{z} + p_{E x 3} d f_{z}^{2}) [1 - p_{E x 4} sgn (κ_{x})] λ_{E x} \\ K_{x κ} = F_{z} (p_{K x 1} + p_{K x 2} d f_{z}) exp (p_{Kx3} d f_{z}) (1 + p_{p x 1} d p_{i} + p_{p x 2} d p_{i}^{2}) \\ B_{x} = K_{x κ} / (C_{x} D_{x} + ε_{x}) \\ S_{H x} = p_{H x 1} + p_{H x 2} d f_{z} \\ S_{V x} = F_{z} \cdot (p_{V x 1} + p_{V x 2} d f_{z}) λ_{V x} λ^{'}_{μ x} ς_{1} \end{array}$

_SHx и _SVx представляют смещения к скользящей и продольной силе в функции скольжения силы или горизонтальные и вертикальные смещения, если функция нанесена как кривая. _μx - коэффициент трения, зависящий от продольной нагрузки. _εx маленькое число, вставленное для предотвращения деления на нули, когда _Fz приближается к нулю.

Вертикальная динамика

Если вы не выбираете вертикальные степени свободы путем установки Vertical Motion на Noneблок передает приложенные силы шасси непосредственно к расчетам сопротивления качению и продольной силы.

Если вы задаете Vertical Motion Mapped stiffness and dampingвертикальное движение зависит от жесткости колеса и демпфирования. Жесткость является функцией перемещения боковой стенки шины и давления. Демпфирование является функцией скорости и давления боковой стенки шины.

$F z t i r e (z, \dot{z}, P_{t i r e}) = F_{z k} (z, P_{t i r e}) + F_{z b} (\dot{z}, P_{t i r e})$

Блок определяет вертикальную характеристику, используя это дифференциальное уравнение.

$\ddot{z} m = F z t i r e - F_{z} - m g$

Когда вы отключаете вертикальную степень свободы, входная нормальная сила от транспортного средства переходит непосредственно к вычислениям продольной и силы качения.

$\begin{array}{l} \ddot{z} = \dot{z} = m = 0 \\ F z t i r e = m g \end{array}$

Блок использует фиксированную систему координат колеса, чтобы разрешить вертикальные силы.

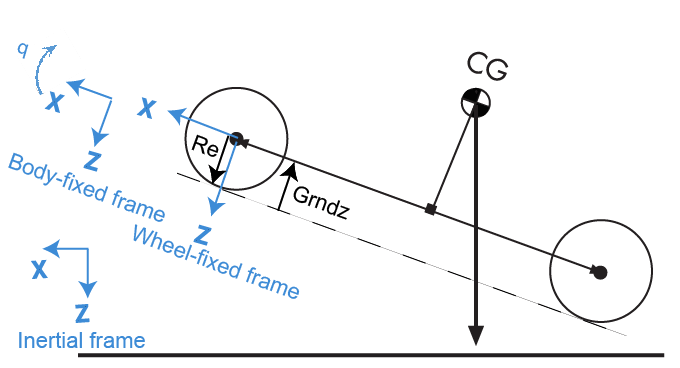
Figure of inclined plan with tires and body-fixed, wheel-fixed, and inertial frames

В уравнениях используются эти переменные.

Fztire	Нормальная сила шины вдоль фиксированной оси Z колеса
m	Масса оси
_Fzk	Нормальная сила шины из-за жесткости колеса вдоль фиксированной оси Z колеса
_Fzb	Нормальная сила шины от демпфирования колеса вдоль фиксированной оси Z колеса
_Fz	Подвеска или нормальная сила транспортного средства вдоль фиксированной оси Z колеса
_PTire	Давление в шинах
$z, \dot{z}, \ddot{z}$	Перемещение, скорость и ускорение шины, соответственно, вдоль фиксированной оси Z колеса

Учет степени

Для учета степени, блок реализует эти уравнения.

Сигнал шины			Описание	Уравнения
`PwrInfo`	`PwrTrnsfrd` - Степень между блоками Положительные сигналы указывают на поток в блок Отрицательные сигналы указывают на выход из блока	`PwrRoad`	Тяговая степень, приложенная к оси	$P_{r o a d} = F_{x} V_{x}$
		`PwrAxlTrq`	Внешний крутящий момент, приложенный осью к колесу	$P_{T} = T ω$
		`PwrFz`	Вертикальное усилие, приложенное к колесу транспортным средством или подвеской	$P_{F z} = F_{z} \dot{z}$
	`PwrNotTrnsfrd` - Степень через контур блока, но не переданный Положительные сигналы указывают на вход Отрицательные сигналы указывают на потерю	`PwrSlip`	Тяговые потери степени	$P_{κ} = F_{x} V_{x} + (- F_{c p} R_{e} + M_{y}) ω$
		`PwrMyRoll`	Степень сопротивления качения	$P_{M y} = M_{y} ω$
		`PwrMyBrk`	Тормозные степени	$P_{b r k} = M_{b r k} ω$
		`PwrMyb`	Потери вязкого демпфирования качения	$P_{b} = - b ω^{2}$
		`PwrFzDamp`	Вертикальная демпфирующая степень	$P_{F z b} = F_{z b} \dot{z}$
	`PwrStored` - Сохраненная скорость изменения энергии Положительные сигналы указывают на увеличение Отрицательные сигналы указывают на уменьшение	`PwrStoredzdot`	Скорость изменения вертикальной кинетической энергии	$P_{\dot{z}} = m \ddot{z} \dot{z}$
		`PwrStoredq`	Скорость изменения вращательной кинетической энергии	$P_{ω} = I_{y y} \dot{ω} ω$
		`PwrStoredFsFzSprng`	Скорость изменения потенциальной энергии накопленной боковой стенки	$P_{F z k} = F_{z k} {\dot{z}}_{x}$
		`PwrStoredGrvty`	Скорость изменения энергии гравитационного потенциала	$P_{g} = - m g \dot{Z}$

В уравнениях используются эти переменные.

ω	Скорость вращения колеса
b	Компонент линейной силы скорости
_Fx	Продольная сила, развиваемая интерфейсом дороги шины из-за скольжения
_Fcp	Сила скольжения шины на контактной закрашенной фигуре
_Fz	Нормальная сила транспортного средства
_Fzb	Нормальная сила шины из-за демпфирования колеса
_Fzk	Нормальная сила шины из-за жесткости колеса
_Iyy	Инерция вращения колеса
_Mbrk	Тормозной момент
_My	Крутящий момент сопротивления качению
_Re	Эффективный радиус шины при нагрузке и при заданном давлении
T	Крутящий момент оси, приложенный к колесу
_Vx	Скорость продольной оси
$z, \dot{z}, \ddot{z}$	Перемещение, скорость и ускорение шины, соответственно
ω	Скорость вращения колеса
$\dot{Z}$	Вертикальная скорость транспортного средства вдоль фиксированной оси Z

Порты

Вход

расширить все

`BrkPrs` - Давление торможения
`scalar`

Давление торможения, в Па.

Зависимости

Чтобы включить этот порт, для параметра Brake Type задайте один из следующих типов:

Disc
Drum
Mapped

`AxlTrq` - Крутящий момент на оси
`scalar`

Крутящий момент оси, _Ta, вокруг оси вращения колеса, в Н· м.

`Vx` - Скорость
`scalar`

Продольная скорость оси вдоль транспортного средства (кузова) - по оси X, в м/с.

`Fz` - Нормальная сила
`scalar`

Абсолютное значение нормальной силы подвески или транспортного средства вдоль фиксированной оси Z кузова, в Н.

`Gnd` - Перемещение грунта
`scalar`

Перемещение грунта, Grndz, по отрицательной оси Z с фиксированным колесом, в м.

Figure of inclined plan with tires and body-fixed, wheel-fixed, and inertial frames

Зависимости

Создание Gnd:

Установите Vertical Motion значение Mapped stiffness and damping.
На панели Vertical выберите Input ground displacement.

`lam_mux` - Коэффициент масштабирования трения
`scalar`

Коэффициент масштабирования продольного трения, безразмерный.

Зависимости

Чтобы включить этот порт, выберите Input friction scale factor.

`TirePrs` - Давление в шинах
`scalar`

Давление в шинах, в Па.

Зависимости

Чтобы включить этот порт:

Установите один из следующих параметров:
- Longitudinal Force с Magic Formula pure longitudinal slip.
- Rolling Resistance с Pressure and velocity или Magic Formula.
- Vertical Motion с Mapped stiffness and damping.
На панели Wheel Dynamics выберите Input tire pressure.

`Tamb` - Температура окружающей среды
`scalar`

Температура окружающей среды, _Tamb, в К.

Зависимости

Чтобы включить этот порт:

Установите Rolling Resistance значение ISO 28580.
На панели Rolling Resistance выберите для Input ambient temperature.

Выход

расширить все

`Info` - Сигнал шины
автобус

Сигнал шины, содержащий эти вычисления блоков.

Сигнал			Описание	Модули
`AxlTrq`			Крутящий момент оси вокруг неподвижной оси Y тела	Н· м
`Omega`			Скорость вращения колеса вокруг фиксированной по оси Y тела	рад/с
`Omegadot`			Угловое ускорение колеса вокруг фиксированной по оси Y тела	рад/с ^ 2
`Fx`			Продольная сила транспортного средства вдоль фиксированной по оси X кузова	N
`Fz`			Вертикальная сила транспортного средства вдоль фиксированной оси Z кузова	N
`Fzb`			Нормальная сила шины от демпфирования колеса вдоль фиксированной оси Z колеса	N
`Fzk`			Нормальная сила шины из-за жесткости колеса вдоль фиксированной оси Z колеса	N
`My`			Крутящий момент сопротивления качению вокруг оси Y тела	Н· м
`Myb`			Крутящий момент сопротивления качению из-за демпфирования вокруг фиксированной по оси Y тела	Н· м
`Kappa`			Коэффициент скольжения	НА
`Vx`			Продольная скорость транспортного средства вдоль фиксированной по оси X кузова	м/с
`Re`			Эффективный радиус колеса вдоль фиксированной оси Z	m
`BrkTrq`			Момент привода вокруг оси Y тела	Н· м
`BrkPrs`			Давление торможения	Pa
`z`			Вертикальное отклонение колеса вдоль фиксированной оси Z колеса	m
`zdot`			Вертикальная скорость колеса вдоль фиксированной оси Z колеса	м/с
`zddot`			Вертикальное ускорение колеса вдоль фиксированной оси Z колеса	м/с ^ 2
`Gndz`			Перемещение земли вдоль отрицательного значения фиксированной по оси Z колеса (положительный вход создает подъем колеса)	m
`GndFz`			Вертикальное усилие колеса на земле вдоль отрицательного значения фиксированной оси Z колеса	N
`TirePrs`			Давление в шинах	Pa
`Fpatch`			Тяговая степень, приложенная к оси
`PwrInfo`	`PwrTrnsfrd`	`PwrRoad`	Внешний крутящий момент, приложенный осью к колесу	W
		`PwrAxlTrq`	Вертикальное усилие, приложенное к колесу транспортным средством или подвеской	W
		`PwrFz`	Тяговые потери степени	W
	`PwrNotTrnsfrd`	`PwrSlip`	Степень сопротивления качения	W
		`PwrMyRoll`	Тормозные степени	W
		`PwrMyBrk`	Потери вязкого демпфирования качения	W
		`PwrMyb`	Вертикальная демпфирующая степень	W
		`PwrFzDamp`	Скорость изменения вертикальной кинетической энергии	W
	`PwrStored`	`PwrStoredzdot`	Скорость изменения вращательной кинетической энергии	W
		`PwrStoredq`	Скорость изменения потенциальной энергии накопленной боковой стенки	W
		`PwrStoredFsFzSprng`	Скорость изменения энергии гравитационного потенциала	W
		`PwrStoredGrvty`	Тяговая степень, приложенная к оси	W

`Fx` - Сила продольной оси
`scalar`

Продольная сила, действующая на ось, вдоль фиксированной по оси X кузова, в N. Положительная сила, действующая на движение транспортного средства вперед.

`Omega` - скорость вращения колеса
`scalar`

Скорость вращения колеса, вокруг фиксированной по оси Y тела, в рад/с.

`z` - Вертикальное отклонение колеса
`scalar`

Вертикальное отклонение колеса вдоль фиксированной по оси Z колеса, в м.

Зависимости

Чтобы включить этот порт, установите Vertical Motion равным Mapped stiffness and damping.

`zdot` - Вертикальная скорость колеса
`scalar`

Вертикальная скорость колеса вдоль фиксированной по оси Z колеса, в м/с.

Зависимости

Чтобы включить этот порт, установите Vertical Motion равным Mapped stiffness and damping.

Параметры

расширить все

Опции блока

`Longitudinal Force` - Выбор типа
`Magic Formula constant value` (по умолчанию) | `Magic Formula pure longitudinal slip` | `Mapped force`

Настройка	Реализация блока
`Magic Formula constant value`	Магическая формула с постоянным коэффициентом жесткости, формы, пика и кривизны.
`Magic Formula pure longitudinal slip`	Магическая формула с зависимыми от нагрузки коэффициентами, которые реализуют уравнения 4.E9 через 4.E18 в Шине и Динамике аппарата.
`Mapped force`	Интерполяционная таблица, которая является функцией нормальной силы и коэффициента скольжения колеса.

Зависимости

Выбор Включает эти параметры

Выбор	Включает эти параметры
`Magic Formula constant value`	Pure longitudinal peak factor, Dx Pure longitudinal shape factor, Cx Pure longitudinal stiffness factor, Bx Pure longitudinal curvature factor, Ex
`Magic Formula pure longitudinal slip`	Cfx shape factor, PCX1 Longitudinal friction at nominal normal load, PDX1 Frictional variation with load, PDX2 Frictional variation with camber, PDX3 Longitudinal curvature at nominal normal load, PEX1 Variation of curvature factor with load, PEX2 Variation of curvature factor with square of load, PEX3 Longitudinal curvature factor with slip, PEX4 Longitudinal slip stiffness at nominal normal load, PKX1 Variation of slip stiffness with load, PKX2 Slip stiffness exponent factor, PKX3 Horizontal shift in slip ratio at nominal normal load, PHX1 Variation of horizontal slip ratio with load, PHX2 Vertical shift in load at nominal normal load, PVX1 Variation of vertical shift with load, PVX2 Linear variation of longitudinal slip stiffness with tire pressure, PPX1 Quadratic variation of longitudinal slip stiffness with tire pressure, PPX2 Linear variation of peak longitudinal friction with tire pressure, PPX3 Quadratic variation of peak longitudinal friction with tire pressure, PPX4 Linear variation of longitudinal slip stiffness with tire pressure, PPX1 Slip speed decay function scaling factor, lam_muV Brake slip stiffness scaling factor, lam_Kxkappa Longitudinal shape scaling factor, lam_Cx Longitudinal curvature scaling factor, lam_Ex Longitudinal horizontal shift scaling factor, lam_Hx Longitudinal vertical shift scaling factor, lam_Vx
`Mapped force`	Slip ratio breakpoints, kappaFx Normal force breakpoints, FzFx Longitudinal force map, FxMap

Magic Formula constant value

Pure longitudinal peak factor, Dx

Pure longitudinal shape factor, Cx

Pure longitudinal stiffness factor, Bx

Pure longitudinal curvature factor, Ex

Magic Formula pure longitudinal slip

Cfx shape factor, PCX1

Longitudinal friction at nominal normal load, PDX1

Frictional variation with load, PDX2

Frictional variation with camber, PDX3

Longitudinal curvature at nominal normal load, PEX1

Variation of curvature factor with load, PEX2

Variation of curvature factor with square of load, PEX3

Longitudinal curvature factor with slip, PEX4

Longitudinal slip stiffness at nominal normal load, PKX1

Variation of slip stiffness with load, PKX2

Slip stiffness exponent factor, PKX3

Horizontal shift in slip ratio at nominal normal load, PHX1

Variation of horizontal slip ratio with load, PHX2

Vertical shift in load at nominal normal load, PVX1

Variation of vertical shift with load, PVX2

Linear variation of longitudinal slip stiffness with tire pressure, PPX1

Quadratic variation of longitudinal slip stiffness with tire pressure, PPX2

Linear variation of peak longitudinal friction with tire pressure, PPX3

Quadratic variation of peak longitudinal friction with tire pressure, PPX4

Linear variation of longitudinal slip stiffness with tire pressure, PPX1

Slip speed decay function scaling factor, lam_muV

Brake slip stiffness scaling factor, lam_Kxkappa

Longitudinal shape scaling factor, lam_Cx

Longitudinal curvature scaling factor, lam_Ex

Longitudinal horizontal shift scaling factor, lam_Hx

Longitudinal vertical shift scaling factor, lam_Vx

Mapped force

Slip ratio breakpoints, kappaFx

Normal force breakpoints, FzFx

Longitudinal force map, FxMap

`Rolling Resistance` - Выбор типа
`None` (по умолчанию) | `Pressure and velocity` | `ISO 28580` | `Magic Formula` | `Mapped torque`

Чтобы вычислить крутящий момент сопротивления качению, задайте один из следующих Rolling Resistance параметров.

Настройка	Реализация блока
`None`	Ничего
`Pressure and velocity`	Метод в методике ступенчатого прибрежного бурения для измерения сопротивления качению шин. Сопротивление качению является функцией давления в шине, нормальной силы и скорости.
`ISO 28580`	Метод, указанный в ISO 28580:2018, Метод измерения сопротивления качению легковых, грузовых и автобусных шин - Однофазная точка тест и корреляция результатов измерений.
`Magic Formula`	Магические формульные уравнения из 4.E70 в Tire и Динамику аппарата. Магическая формула является эмпирическим уравнением, основанным на аппроксимационных коэффициентах.
`Mapped torque`	Интерполяционная таблица, которая является функцией от нормальной силы и продольной скорости оси спина.

Зависимости

Выбор	Параметры
`Pressure and velocity`	Velocity independent force coefficient, aMy Linear velocity force component, bMy Quadratic velocity force component, cMy Tire pressure exponent, alphaMy Normal force exponent, betaMy
`ISO 28580`	Parasitic losses force, Fpl Rolling resistance constant, Cr Thermal correction factor, Kt Measured temperature, Tmeas Parasitic losses force, Fpl Ambient temperature, Tamb
`Magic Formula`	Rolling resistance torque coefficient, QSY Longitudinal force rolling resistance coefficient, QSY2 Linear rotational speed rolling resistance coefficient, QSY3 Quartic rotational speed rolling resistance coefficient, QSY4 Camber squared rolling resistance torque, QSY5 Load based camber squared rolling resistance torque, QSY6 Normal load rolling resistance coefficient, QSY7 Pressure load rolling resistance coefficient, QSY8 Rolling resistance scaling factor, lam_My
`Mapped torque`	Spin axis velocity breakpoints, VxMy Normal force breakpoints, FzMy Rolling resistance torque map, MyMap

`Brake Type` - Выбор типа
`None` | `Disc` | `Drum` | `Mapped`

Существует четыре типа блоков Longitudinal Wheel. Каждый блок реализует свой тип тормоза.

Имя блока	Настройка типа тормоза	Реализация тормозов
Longitudinal Wheel - No Brake	`None`	Ничего
Longitudinal Wheel - Disc Brake	`Disc`	Тормоз, который преобразует давление в тормозном цилиндре в тормозное усилие.
Longitudinal Wheel - Drum Brake	`Drum`	Барабанный тормоз Simplex, который преобразует приложенную силу и геометрию тормоза в сетевой тормозной крутящий момент.
Longitudinal Wheel - Mapped Brake	`Mapped`	Интерполяционная таблица, которая является функцией скорости и прикладываемого тормозного давления колеса.

`Vertical Motion` - Выбор типа
`None` (по умолчанию) | `Mapped stiffness and damping`

Чтобы вычислить вертикальное движение, задайте один из следующих Vertical Motion параметров.

Настройка	Реализация блока
`None`	Блок передает приложенные силы шасси непосредственно к вычислениям сопротивления качению и продольной силы.
`Mapped stiffness and damping`	Вертикальное движение зависит от жесткости колеса и демпфирования. Жесткость является функцией перемещения боковой стенки шины и давления. Демпфирование является функцией скорости и давления боковой стенки шины.

Выбор Включает эти параметры Создает эти выходные порты

Выбор	Включает эти параметры	Создает эти выходные порты
`Mapped stiffness and damping`	Wheel and unsprung mass, m Initial deflection, zo Initial velocity, zdoto Gravitational acceleration, g Vertical deflection breakpoints, zFz Pressure breakpoints, pFz Force due to deflection, Fzz Vertical velocity breakpoints, zdotFz Force due to velocity, Fzzdot Ground displacement, Gndz Input ground displacement	`z` `zdot`

Mapped stiffness and damping

Wheel and unsprung mass, m

Initial deflection, zo

Initial velocity, zdoto

Gravitational acceleration, g

Vertical deflection breakpoints, zFz

Pressure breakpoints, pFz

Force due to deflection, Fzz

Vertical velocity breakpoints, zdotFz

Force due to velocity, Fzzdot

Ground displacement, Gndz

Input ground displacement

z

zdot

`Longitudinal scaling factor, lam_x` - Коэффициент масштабирования трения
`1` (по умолчанию)

Коэффициент масштабирования продольного трения, безразмерный.

Зависимости

Чтобы включить этот параметр, очистите Input friction scale factor.

`Input friction scale factor` - Выбор
`Off` (по умолчанию)

Создайте входной порт для коэффициента масштабирования продольного трения.

Зависимости

Выбор этого параметра:

Создает входной порт lam_mux.
Отключает Longitudinal scaling factor, lam_x параметра.

Динамика колеса

`Axle viscous damping coefficient, br` - Демпфирование
`0.001` (по умолчанию) | `scalar`

Коэффициент вязкого демпфирования оси, br, в Н· м· с/рад.

`Wheel inertia, Iyy` - Инерция
`0.8` (по умолчанию) | `scalar`

Инерция колеса, в кг· м ^ 2.

`Wheel initial angular velocity, omegao` - Скорость колеса
`0` (по умолчанию) | `scalar`

Начальная скорость вращения колеса, вдоль фиксированной по оси Y тела, в рад/с.

`Relaxation length, Lrel` - Длина релаксации
`0.5` (по умолчанию) | `scalar`

Длина релаксации колес, в м.

`Loaded radius, Re` - Загруженный радиус
`0.3` (по умолчанию) | `scalar`

Радиус нагруженного колеса, Re, в м.

Figure of inclined plan with tires and body-fixed, wheel-fixed, and inertial frames

`Unloaded radius, UNLOADED_RADIUS` - Разгруженный радиус
`0.4` (по умолчанию) | `scalar`

Радиус разгружаемого колеса, в м.

Зависимости

Чтобы создать этот параметр, установите Rolling Resistance равным Pressure and velocity или Magic Formula.

`Nominal longitudinal speed, LONGVL` - Скорость
`16` (по умолчанию) | `scalar`

Номинальная продольная скорость вдоль фиксированной по телу оси X, в м/с.

Зависимости

Чтобы включить этот параметр, установите Longitudinal Force равным Magic Formula pure longitudinal slip.

`Nominal camber angle, gamma` - Camber
`0` (по умолчанию) | `scalar`

Номинальный угол развала, в рад.

Зависимости

Чтобы включить этот параметр, установите либо:

Longitudinal Force с Magic Formula pure longitudinal slip.
Rolling Resistance с Magic Formula.

`Nominal pressure, NOMPRES` - Давление
`220000` (по умолчанию) | `scalar`

Номинальное давление, в Па.

Зависимости

Чтобы включить этот параметр, установите либо:

Longitudinal Force с Magic Formula pure longitudinal slip.
Rolling Resistance с Magic Formula.

`Pressure, press` - Давление
`220000` (по умолчанию) | `scalar`

Давление, в Па.

Зависимости

Чтобы включить этот параметр:

Установите одно из следующих:
- Longitudinal Force с Magic Formula pure longitudinal slip.
- Rolling Resistance с Pressure and velocity или Magic Formula.
- Vertical Motion с Mapped stiffness and damping.
На панели Wheel Dynamics очистите Input tire pressure.

Продольный

Магия Формулы Константа Значение

`Pure longitudinal peak factor, Dx` - Коэффициент
`1` (по умолчанию) | `scalar`

Чистый продольный пиковый коэффициент, безразмерный.

Поверхность	B	C	D	E
Сухой тармак	10	1.9	1	0.97
Мокрый тармак	12	2.3	0.82	1
Снег	5	2	0.3	1
Лед	4	2	0.1	1

Зависимости

Чтобы создать этот параметр, выберите параметр Longitudinal Force Magic Formula constant value.

`Pure longitudinal shape factor, Cx` - Коэффициент
`1.65` (по умолчанию) | `scalar`

Чистый продольный масштабный фактор, безразмерная.

Поверхность	B	C	D	E
Сухой тармак	10	1.9	1	0.97
Мокрый тармак	12	2.3	0.82	1
Снег	5	2	0.3	1
Лед	4	2	0.1	1

Зависимости

Чтобы создать этот параметр, выберите параметр Longitudinal Force Magic Formula constant value.

`Pure longitudinal stiffness factor, Bx` - Коэффициент
`10` (по умолчанию) | `scalar`

Чистый коэффициент продольной жесткости, безразмерный.

Поверхность	B	C	D	E
Сухой тармак	10	1.9	1	0.97
Мокрый тармак	12	2.3	0.82	1
Снег	5	2	0.3	1
Лед	4	2	0.1	1

Зависимости

Чтобы создать этот параметр, выберите параметр Longitudinal Force Magic Formula constant value.

`Pure longitudinal curvature factor, Ex` - Коэффициент
`0.01` (по умолчанию) | `scalar`

Чистый коэффициент продольной кривизны, безразмерный.

Поверхность	B	C	D	E
Сухой тармак	10	1.9	1	0.97
Мокрый тармак	12	2.3	0.82	1
Снег	5	2	0.3	1
Лед	4	2	0.1	1

Зависимости

Чтобы создать этот параметр, выберите параметр Longitudinal Force Magic Formula constant value.

Магия Формула Чистый Продольный Скольжение