Combined Slip Wheel 2DOF

Комбинированное скольжение 2DOF колесом с диском, барабаном или картографическим тормозом

Библиотека:
Динамика автомобиля Blockset/Колеса и шины

Описание

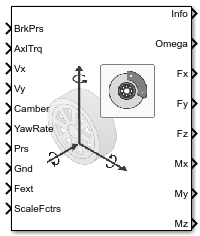
Блок Combined Slip Wheel 2DOF реализует продольное и боковое поведение колеса, характеризующегося Магической формулой^{[1] and [2]}. Можно импортировать собственные данные о шинах или использовать установленные наборы данных о шинах, предоставленные Глобальным центром симуляции эффективности автомобиля (GCAPS). Используйте блок в симуляциях привода и транспортного средства, где требуется низкочастотная шина-дорога и тормозные силы, чтобы определить транспортное средство ускорение, торможение и сопротивление качению колеса. Блок подходит для приложений, которые требуют комбинированного бокового скольжения, например, в исследованиях бокового движения и устойчивости рыскания.

На основе крутящего момента на приводе, давления тормоза, высоты дороги, угла развала колеса и давления надувания, блок определяет скорость вращения колеса, вертикальное движение, силы и моменты во всех шести степенях свободы (DOF). Используйте вертикальный СТЕПЕНЬ СВОБОДЫ, чтобы изучить резонансы подвески шин от профилей дорог или движения шасси.

Используйте параметр Tire type, чтобы выбрать источник данных о шинах.

Цель Действие

Цель	Действие
Реализуйте Магическую формулу с помощью эмпирических уравнений^{[1] and [2]}. В уравнениях используются аппроксимационные коэффициенты, которые соответствуют параметрам блоков.	Обновите параметры блоков с помощью коэффициентов аппроксимации из файла: Установите Tire type значение `External file`. На панели Wheel and Tire Parameters > Tire выберите Select file. Выберите файл коэффициентов шины. Выберите Update mask values from file. В диалоговом окне с запросом подтверждения нажмите OK. Блок обновляет параметры. Выберите Apply.
Реализуйте установленные наборы данных о шинах, предоставленные Глобальным центром симуляции эффективности автомобиля (GCAPS).	Обновите применимые параметры блоков с помощью GCAPS установленной шины данных: Установите Tire type на шину, которую вы хотите реализовать. Опции включают: `Light passenger car 205/60R15` `Mid-size passenger car 235/45R18` `Performance car 225/40R19` `SUV 265/50R20` `Light truck 275/65R18` `Commercial truck 295/75R22.5` Выберите Update applicable Tire Parameters with tire type values. На вкладке Tire Parameters блок обновляет применимые параметры, включая Wheel width, Rim radius и Wheel mass. Выберите Apply.

Реализуйте Магическую формулу с помощью эмпирических уравнений^{[1] and [2]}. В уравнениях используются аппроксимационные коэффициенты, которые соответствуют параметрам блоков.

Обновите параметры блоков с помощью коэффициентов аппроксимации из файла:

Установите Tire type значение External file.
На панели Wheel and Tire Parameters > Tire выберите Select file.
Выберите файл коэффициентов шины.
Выберите Update mask values from file. В диалоговом окне с запросом подтверждения нажмите OK. Блок обновляет параметры.
Выберите Apply.

Реализуйте установленные наборы данных о шинах, предоставленные Глобальным центром симуляции эффективности автомобиля (GCAPS).

Обновите применимые параметры блоков с помощью GCAPS установленной шины данных:

Установите Tire type на шину, которую вы хотите реализовать. Опции включают:
- Light passenger car 205/60R15
- Mid-size passenger car 235/45R18
- Performance car 225/40R19
- SUV 265/50R20
- Light truck 275/65R18
- Commercial truck 295/75R22.5
Выберите Update applicable Tire Parameters with tire type values. На вкладке Tire Parameters блок обновляет применимые параметры, включая Wheel width, Rim radius и Wheel mass.
Выберите Apply.

Используйте параметр Brake Type, чтобы выбрать тормоз.

Цель	Настройка типа тормоза
Нет торможения	`None`
Реализуйте тормоз, который преобразует давление в тормозном цилиндре в тормозную силу	`Disc`
Реализуйте симплексный барабанный тормоз, который преобразует приложенную силу и геометрию тормоза в сетевой тормозной крутящий момент	`Drum`
Реализуйте интерполяционную таблицу, которая является функцией скорости и прикладываемого тормозного давления колеса	`Mapped`

Динамика Вращательного Колеса

Блок вычисляет инерционную характеристику колеса, удовлетворяющего:

Потери на оси
Тормозной и приводной крутящий момент
Сопротивление качению шин
Контакт заземления через интерфейс шина-дорога

Чтобы реализовать Магическую формулу, блок использует эти уравнения.

Вычисление	Уравнения
Продольная сила	Динамика аппарата^[2] уравнения с 4.E9 по 4.E57
Боковая сила - чистая боковая кромка	Динамика аппарата^[2] уравнения с 4.E19 по 4.E30
Боковая сила - комбинированное скольжение	Динамика аппарата^[2] уравнения с 4.E58 по 4.E67
Вертикальная динамика	Динамика аппарата^[2] уравнения 4.E68, 4.E1, 4.E2a и 4.E2b
Опрокидывающая пара	Динамика аппарата^[2] уравнение 4.E69
Сопротивление качению	Улучшенная модель Magic Formula/Swift шины, которая может справиться с скачками давления инфляции^[1] уравнение 6.1.2 Динамика аппарата^[2] уравнение 4.E70
Выравнивающий момент	Динамика аппарата^[2] уравнение 4.E31 по 4.E49
Центрирующий крутящий момент - комбинированное скольжение	Динамика аппарата^[2] уравнение 4.E71 по 4.E78

Входной крутящий момент является суммированием приложенного крутящего момента оси, тормозного момента и момента, возникающего из-за объединенного крутящего момента шины.

$T_{i} = T_{a} - T_{b} + T_{d}$

На момент, вытекающий из комбинированного крутящего момента шины, блок реализует силы тягового колеса и сопротивление качению с динамикой первого порядка. Сопротивление качению имеет постоянную по времени, параметризованную с точки зрения длины релаксации.

$T_{d} (s) = \frac{1}{\frac{| ω | R_{e}}{L_{e}} s + 1} (F_{x} R_{e} + M_{y})$

Если тормоза включены, блок определяет условие блокировки или разблокировки торможения на основе идеализированной модели трения сухой муфты. На основе условия блокировки блок реализует эти модели трения и динамики.

Если	Условие блокировки	Модель трения	Динамическая модель
$\begin{array}{l} ω \neq 0 \\ или \\ T_{S} < \| T_{i} + T_{f} - ω b \| \end{array}$	Незапертый	$\begin{array}{l} T_{f} = T_{k} \\ где, \\ T_{k} = F_{c} R_{e f f} μ_{k} \tanh [4 (- ω_{d})] \\ T_{s} = F_{c} R_{e f f} μ_{s} \\ R_{e f f} = \frac{2 (R_{o}^{3} - R_{i}^{3})}{3 (R_{o}^{2} - R_{i}^{2})} \end{array}$	$\dot{ω} J = - ω b + T_{i} + T_{o}$
$\begin{array}{l} ω = 0 \\ и \\ T_{S} \geq \| T_{i} + T_{f} - ω b \| \end{array}$	Запертый	$T_{f} = T_{s}$	$ω = 0$

В уравнениях используются эти переменные.

ω	Скорость вращения колеса
a	Независимая от скорости сила компонента
b	Компонент линейной силы скорости
c	Квадратичная сила скорости компонента
_Le	Длина релаксации шин
J	Момент инерции
_My	Крутящий момент сопротивления качению
_Ta	Приложенный крутящий момент оси вокруг оси вращения колеса
_Tb	Тормозной крутящий момент
_Td	Комбинированный крутящий момент в шинах
_Tf	Фрикционный крутящий момент
_Ti	Крутящий момент входа сети
_Tk	Кинетический фрикционный крутящий момент
_To	Крутящий момент выхода сети
_Ts	Статический крутящий момент трения
_Fc	Приложенная сила сцепления
_Fx	Продольная сила, развиваемая интерфейсом дороги шины из-за скольжения
_Reff	Эффективный радиус сцепления
_Ro	Внешний радиус кольцевого диска
_Ri	Внутренний радиус кольцевого диска
_Re	Эффективный радиус шины при нагрузке и при заданном давлении
_Vx	Скорость продольной оси
_Fz	Нормальная сила транспортного средства
ɑ	Экспонента давления в шинах
β	Нормальная экспонента силы
_pi	Давление в шинах
_μs	Коэффициент статического трения
_μk	Коэффициент кинетического трения

Системы координат шин и колес

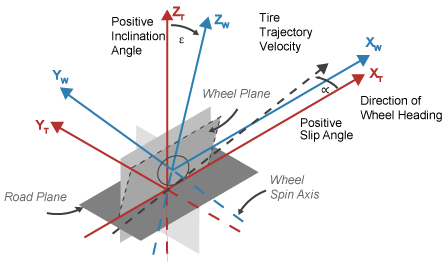
Чтобы разрешить силы и моменты, блок использует ориентацию Z-Up для систем координат шины и колеса.

Оси систем координат шин (_XT, _YT, _ZT) фиксируются в опорной системе координат, присоединенной к шине. Источник находится в контакте шины с землей.
Оси системы координат колеса (_XW, _YW, _ZW) фиксируются в опорной раме, прикрепленной к колесу. Источник находится в центре колеса.

Ориентация по оси Z^[1]

Z-Up tire and wheel coordinate systems showing wheel plane and road plane

Тормоза

Диск

Если вы задаете параметр Brake Type Discблок реализует дисковый тормоз. Этот рисунок показывает вид сбоку и спереди дискового тормоза.

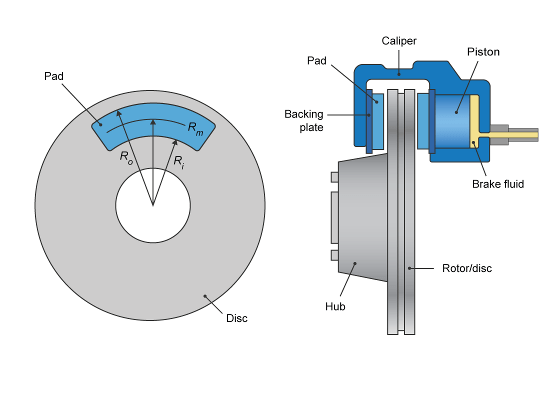
Front and side view of disc brake, showing pad, disc, and caliper

Дисковый тормоз преобразует давление в тормозном цилиндре из тормозного цилиндра в усилие. Дисковый тормоз прикладывает силу к среднему радиусу тормозной колодки.

Блок использует эти уравнения, чтобы вычислить момент привода для дискового тормоза.

$T = {\begin{matrix} \frac{μ P π B_{a}^{2} R_{m} N_{p a d s}}{4} когда N \neq 0 \\ \frac{μ_{s t a t i c} P π B_{a}^{2} R_{m} N_{p a d s}}{4} когда N = 0 \end{matrix}$

$R m = \frac{R o + R i}{2}$

В уравнениях используются эти переменные.

T	Момент привода
P	Прикладываемое тормозное давление
N	Скорость колеса
_Npads	Количество тормозных колодок в узле дискового тормоза
_μstatic	Коэффициент статического трения пары диск-колодка
μ	Коэффициент кинетического трения пары диск-колодка
_Ba	Внутренний диаметр тормозного цилиндра суппорта
_Rm	Средний радиус приложения силы тормозной колодки на роторе тормоза
_Ro	Внешний радиус тормозной колодки
_Ri	Внутренний радиус тормозной колодки

Барабан

Если вы задаете параметр Brake Type Drum, блок реализует статический (статический) симплексный барабанный тормоз. Симплексный барабанный тормоз состоит из одного двустороннего гидравлического привода и двух тормозных колодок. Тормозные колодки не имеют общего шарнирного контакта.

Модель симплексного барабанного тормоза использует приложенную силу и геометрию тормоза, чтобы вычислить крутящий момент привода для каждой тормозной колодки. Модель барабана принимает, что приводы и геометрия башмака симметричны для обеих сторон, позволяя использовать один набор геометрии и параметров трения для обеих башмаков.

Блок реализует уравнения, которые получают из этих уравнений в Основах Элементов Машины.

$\begin{array}{l} T_{r s h o e} = (\frac{π μ c r (\cos θ_{2} - \cos θ_{1}) B_{a}^{2}}{2 μ (2 r (\cos θ_{2} - \cos θ_{1}) + a (\cos^{2} θ_{2} - \cos^{2} θ_{1})) + a r (2 θ_{1} - 2 θ_{2} + \sin 2 θ_{2} - \sin 2 θ_{1})}) P \\ T_{l s h o e} = (\frac{π μ c r (\cos θ_{2} - \cos θ_{1}) B_{a}^{2}}{- 2 μ (2 r (\cos θ_{2} - \cos θ_{1}) + a (\cos^{2} θ_{2} - \cos^{2} θ_{1})) + a r (2 θ_{1} - 2 θ_{2} + \sin 2 θ_{2} - \sin 2 θ_{1})}) P \end{array}$

$T = {\begin{matrix} T_{r s h o e} + T_{l s h o e} when N \neq 0 \\ (T_{r s h o e} + T_{l s h o e}) \frac{μ_{s t a t i c}}{μ} когда N = 0 \end{matrix}$

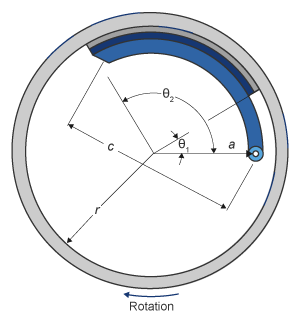
Side view of drum brake

В уравнениях используются эти переменные.

T	Момент привода
P	Прикладываемое тормозное давление
N	Скорость колеса
_μstatic	Коэффициент статического трения пары диск-колодка
μ	Коэффициент кинетического трения пары диск-колодка
_Trshoe	Момент привода правой колодки
_Tlshoe	Момент привода левой колодки
a	Расстояние от центра барабана до шарнира контакта центра башмака
c	Расстояние от шарнира контакта центра колодки до соединения привода тормоза на колодке тормоза
r	Внутренний радиус барабана
_Ba	Внутренний диаметр тормозного цилиндра суппорта
_Θ1	Угол от шарнира контакта центра колодки до начала материала тормозной колодки на колодке
_Θ2	Угол от шарнира контакта центра к концу материала тормозной колодки на колодке

Нанесенный на карту

Если вы задаете параметр Brake Type Mappedблок использует интерполяционную таблицу, чтобы определить момент привода.

$T = {\begin{matrix} f_{b r a k e} (P, N) when N \neq 0 \\ (\frac{μ_{s t a t i c}}{μ}) f_{b r a k e} (P, N) когда N = 0 \end{matrix}$

В уравнениях используются эти переменные.

T	Момент привода
$f_{b r a k e}^{} (P, N)$	Интерполяционная таблица момента привода
P	Прикладываемое тормозное давление
N	Скорость колеса
_μstatic	Коэффициент трения интерфейса «поверхность-поверхность барабана» при статических условиях
μ	Коэффициент трения интерфейса диск-ротор

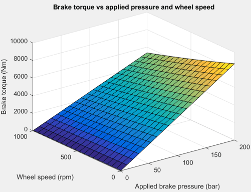
Интерполяционная таблица для крутящего момента привода, $f_{b r a k e}^{} (P, N)$ , является функцией прикладываемого тормозного давления и скорости вращения колеса, где:

T - момент привода, в Н· м.
P прикладываемого тормозного давления, в баре.
N - скорость колеса, в об/мин.

Plot of brake torque as a function of wheel speed and applied brake pressure

Порты

Вход

расширить все

`BrkPrs` - Давление торможения
`scalar` | `N`-by- `1` вектор

Давление торможения, в Па.

Вектор - это количество колес, N, по 1. Если вы задаете скалярное значение, блок принимает, что количество колес равно единице.

Зависимости

Чтобы включить этот порт, для параметра Brake Type задайте один из следующих типов:

Disc
Drum
Mapped

`AxlTrq` - Крутящий момент на оси
`scalar` | `N`-by- `1` вектор

Крутящий момент оси, _Ta, вокруг оси вращения колеса, в Н· м.

`Vx` - Продольная скорость
`scalar` | `N`-by- `1` вектор

Продольная скорость оси, _Vx, вдоль фиксированной по оси X, в м/с.

`Vy` - Поперечная скорость
`scalar` | `N`-by- `1` вектор

Поперечная скорость оси, _Vy, вдоль фиксированной по оси Y шины, в м/с.

`Camber` - Угол развала
`scalar` | `N`-by- `1` вектор

Угол развала, ɣ, в рад.

`YawRate` - скорость вращения шины
`scalar` | `N`-by- `1` вектор

Скорость вращения шины, r, вокруг фиксированной в шине оси Z (скорость рыскания), в рад/с.

`Prs` - Давление наддува шин
`scalar` | `N`-by- `1` вектор

Давление инфляции в шинах, _pi, в Па.

`Gnd` - Перемещение грунта
`scalar` | `N`-by- `1` вектор

Перемещение заземления вдоль неподвижной z оси, в м. Положительный вход обеспечивает подъем колеса.

`Fext` - Сила оси, приложенная к шине
`scalar` | `N`-by- `1` вектор

Сила оси, приложенная к шине, _Fext, вдоль фиксированной осей Z автомобиля (положительный вход сжимает шину), в Н.

`ScaleFctrs` - Масштабные коэффициенты
`27`-by- `N` массив

Шкала фактора «Магическая формула». Измерения массива 27 по количеству колес, N.

Уравнения Магической Формулы используют масштабные коэффициенты для расчета статических или симуляционных изменений во время выполнения. Номинально большинству задано значение 1.

Элемент массива	Переменная	Масштабный коэффициент
`ScaleFctrs(1,1)`	`lam_Fzo`	Номинальная нагрузка
`ScaleFctrs(2,1)`	`lam_mux`	Продольный коэффициент трения
`ScaleFctrs(3,1)`	`lam_muy`	Боковой пиковый коэффициент трения
`ScaleFctrs(4,1)`	`lam_muV`	Скольжение Скорость Vs трения трения
`ScaleFctrs(5,1)`	`lam_Kxkappa`	Жесткость проскальзывания тормоза
`ScaleFctrs(6,1)`	`lam_Kyalpha`	Жесткость поворота
`ScaleFctrs(7,1)`	`lam_Cx`	Продольные масштабные факторы
`ScaleFctrs(8,1)`	`lam_Cy`	Боковые масштабные факторы
`ScaleFctrs(9,1)`	`lam_Ex`	Коэффициент продольной кривизны
`ScaleFctrs(10,1)`	`lam_Ey`	Коэффициент боковой кривизны
`ScaleFctrs(11,1)`	`lam_Hx`	Продольный горизонтальный сдвиг
`ScaleFctrs(12,1)`	`lam_Hy`	Боковой горизонтальный сдвиг
`ScaleFctrs(13,1)`	`lam_Vx`	Продольный вертикальный сдвиг
`ScaleFctrs(14,1)`	`lam_Vy`	Боковой вертикальный сдвиг
`ScaleFctrs(15,1)`	`lam_Kygamma`	Жесткость демпфирующей силы
`ScaleFctrs(16,1)`	`lam_Kzgamma`	Крутящий момент Кэмбера жесткость
`ScaleFctrs(17,1)`	`lam_t`	Пневматический след (коэффициент жесткости крутящего момента)
`ScaleFctrs(18,1)`	`lam_Mr`	Остаточный крутящий момент
`ScaleFctrs(19,1)`	`lam_xalpha`	Альфа-влияние на Fx (каппа)
`ScaleFctrs(20,1)`	`lam_ykappa`	Влияние Каппы на Fy (альфа)
`ScaleFctrs(21,1)`	`lam_Vykappa`	Индуцированное управление слоем Fy
`ScaleFctrs(22,1)`	`lam_s`	Рычаг момента Fx
`ScaleFctrs(23,1)`	`lam_Cz`	Радиальная жесткость шины
`ScaleFctrs(24,1)`	`lam_Mx`	Жесткость опрокидывающей пары
`ScaleFctrs(25,1)`	`lam_VMx`	Вертикальный сдвиг опрокидывающей пары
`ScaleFctrs(26,1)`	`lam_My`	Момент сопротивления качению
`ScaleFctrs(27,1)`	`lam_Mphi`	Крутящий момент при стоянке Mz

Выход

расширить все

`Info` - Блочные данные
автобус

Блочные данные, возвращенные как сигнал шины, содержащий эти значения блоков.

Сигнал	Описание	Модули
`AxlTrq`	Крутящий момент оси вокруг неподвижной оси Y	Н· м
`Omega`	Скорость вращения колеса вокруг фиксированной по оси Y колеса	рад/с
`Fx`	Продольная сила транспортного средства вдоль фиксированной по оси X шины	N
`Fy`	Боковая сила транспортного средства вдоль фиксированной по оси Y шины	N
`Fz`	Вертикальное усилие транспортного средства вдоль фиксированной по оси Z шины	N
`Mx`	Опрокидывающий момент вокруг фиксированной по оси X шины	Н· м
`My`	Крутящий момент сопротивления качению вокруг фиксированной по оси Y шины	Н· м
`Mz`	Выравнивающий момент вокруг фиксированной по оси Z шины	Н· м
`Vx`	Продольная скорость транспортного средства вдоль фиксированной по оси X шины	м/с
`Vy`	Поперечная скорость транспортного средства вдоль фиксированной по оси Y шины	м/с
`Re`	Нагруженный эффективный радиус	m
`Kappa`	Отношение продольных скольжений	НА
`Alpha`	Угол скольжения по стороне	рад
`a`	Контактная закрашенная фигура половинной длины	m
`b`	Контакт с закрашенной фигурой половинной ширины	m
`Gamma`	Угол развала	рад
`psidot`	Скорость вращения шины вокруг фиксированной в шине оси Z (скорость рыскания)	рад/с
`BrkTrq`	Момент привода вокруг фиксированной по оси Y автомобиля	Н· м
`BrkPrs`	Давление торможения	Pa
`z`	Вертикальное перемещение оси вдоль фиксированной оси Z шины	m
`zdot`	Вертикальная скорость оси вдоль фиксированной оси Z шины	м/с
`Gnd`	Перемещение заземления вдоль фиксированной по оси Z шины (положительный вход создает подъем колеса)	m
`GndFz`	Вертикальное усилие боковой стенки на земле вдоль неподвижной оси Z шины	N
`Prs`	Давление надувания шин	Pa

`Omega` - скорость вращения колеса
`scalar` | `N`-by- `1` вектор

Скорость вращения колеса, ω, вокруг фиксированной по оси Y, в рад/с.

`Fx` - Сила продольной оси
`scalar` | `N`-by- `1` вектор

Продольная сила, действующая на ось, _Fx, вдоль фиксированной по оси X шины, в Н. Положительная сила, действующая на перемещение транспортного средства вперед.

`Fy` - Боковая осевая сила
`scalar` | `N`-by- `1` вектор

Боковая сила, действующая на ось, _Fy, вдоль фиксированной по оси Y шины, в Н.

`Fz` - Вертикальная осевая сила
`scalar` | `N`-by- `1` вектор

Вертикальная сила, действующая на ось, _Fz, вдоль фиксированной в шине оси Z, в Н.

`Mx` - Опрокидывающий момент
`scalar` | `N`-by- `1` вектор

Продольный момент, действующий на ось, _Mx, вокруг оси X шины, в N· м.

`My` - Момент сопротивления качению
`scalar` | `N`-by- `1` вектор

Боковой момент, действующий на ось, _My, вокруг оси Y шины, в Н· м.

`Mz` - Выравнивающий момент
`scalar` | `N`-by- `1` вектор

Вертикальный момент, действующий на ось, _Mz, вокруг оси Z шины, в Н· м.

Параметры

расширить все

Опции блока

`Tire Type` - Выбор типа
`External file` (по умолчанию) | `Light passenger car 205/60R15` | `Mid-size passenger car 235/45R18` | `Performance car 225/40R19` | `SUV 265/50R20` | `Light truck 275/65R18` | `Commercial truck 295/75R22.5`

Используйте параметр Tire type, чтобы выбрать источник данных о шинах.

Цель Действие

Цель	Действие
Реализуйте Магическую формулу с помощью эмпирических уравнений^{[1] and [2]}. В уравнениях используются аппроксимационные коэффициенты, которые соответствуют параметрам блоков.	Обновите параметры блоков с помощью коэффициентов аппроксимации из файла: Установите Tire type значение `External file`. На панели Wheel and Tire Parameters > Tire выберите Select file. Выберите файл коэффициентов шины. Выберите Update mask values from file. В диалоговом окне с запросом подтверждения нажмите OK. Блок обновляет параметры. Выберите Apply.
Реализуйте установленные наборы данных о шинах, предоставленные Глобальным центром симуляции эффективности автомобиля (GCAPS).	Обновите применимые параметры блоков с помощью GCAPS установленной шины данных: Установите Tire type на шину, которую вы хотите реализовать. Опции включают: `Light passenger car 205/60R15` `Mid-size passenger car 235/45R18` `Performance car 225/40R19` `SUV 265/50R20` `Light truck 275/65R18` `Commercial truck 295/75R22.5` Выберите Update applicable Tire Parameters with tire type values. На вкладке Tire Parameters блок обновляет применимые параметры, включая Wheel width, Rim radius и Wheel mass. Выберите Apply.

Обновите параметры блоков с помощью коэффициентов аппроксимации из файла:

Установите Tire type значение External file.
На панели Wheel and Tire Parameters > Tire выберите Select file.
Выберите файл коэффициентов шины.
Выберите Update mask values from file. В диалоговом окне с запросом подтверждения нажмите OK. Блок обновляет параметры.
Выберите Apply.

Обновите применимые параметры блоков с помощью GCAPS установленной шины данных:

Установите Tire type на шину, которую вы хотите реализовать. Опции включают:
- Light passenger car 205/60R15
- Mid-size passenger car 235/45R18
- Performance car 225/40R19
- SUV 265/50R20
- Light truck 275/65R18
- Commercial truck 295/75R22.5
Выберите Update applicable Tire Parameters with tire type values. На вкладке Tire Parameters блок обновляет применимые параметры, включая Wheel width, Rim radius и Wheel mass.
Выберите Apply.

`Brake Type` - Выбор типа
`None` | `Disc` | `Drum` | `Mapped`

Используйте параметр Brake Type, чтобы выбрать тормоз.

Цель	Настройка типа тормоза
Нет торможения	`None`
Реализуйте тормоз, который преобразует давление в тормозном цилиндре в тормозную силу	`Disc`
Реализуйте симплексный барабанный тормоз, который преобразует приложенную силу и геометрию тормоза в сетевой тормозной крутящий момент	`Drum`
Реализуйте интерполяционную таблицу, которая является функцией скорости и прикладываемого тормозного давления колеса	`Mapped`

Тормоз

`Static friction coefficient, mu_static` - Статическое трение
`.3` (по умолчанию) | `scalar`

Статический коэффициент трения, без размерности.

Зависимости

Чтобы включить этот параметр, для параметра Brake Type задайте один из следующих типов:

Disc
Drum
Mapped

`Kinetic friction coefficient, mu_kinetic` - Кинетическое трение
`.2` (по умолчанию) | `scalar`

Кинематический коэффициент трения, безразмерный.

Зависимости

Чтобы включить этот параметр, для параметра Brake Type задайте один из следующих типов:

Disc
Drum
Mapped

Диск

`Disc brake actuator bore, disc_abore` - Расстояние между отверстиями
`.05` (по умолчанию) | `scalar`

Отверстие привода дискового тормоза, в м.

Зависимости

Чтобы включить параметры дискового тормоза, выберите Disc для параметра Brake Type.

`Brake pad mean radius, Rm` - Радиус
`.177` (по умолчанию) | `scalar`

Средний радиус тормозной колодки, в м.

Зависимости

Чтобы включить параметры дискового тормоза, выберите Disc для параметра Brake Type.

`Number of brake pads, num_pads` - Количество
`2` (по умолчанию) | `scalar`

Количество тормозных колодок.

Зависимости

Чтобы включить параметры дискового тормоза, выберите Disc для параметра Brake Type.

Барабан