Вычисление вейвлет в каждой возможной шкале - это изрядная работа, и она генерирует ужасное количество данных. Что, если мы выберем только подмножество шкал и позиций, в которых можно делать вычисления?
Оказывается, довольно примечательно, что если мы выберем шкалы и позиции, основанные на степенях двойки - так называемых диадических шкал и позиций - то наш анализ будет намного более эффективным и столь же точным. Такой анализ мы получаем из дискретного вейвлет (DWT). Для получения дополнительной информации о DWT смотрите Алгоритмы в Руководстве пользователя Wavelet Toolbox.
Эффективный способ реализации этой схемы с использованием фильтров был разработан в 1988 году Mallat (см. [Mal89] в ссылки). Алгоритм Mallat на самом деле является классической схемой, известной в сообществе обработки сигналов как двухканальный субдиапазонный кодер (см. страницу 1 книги «Вейвлеты и банки фильтров» Странга и Нгуена [StrN96]).
Этот очень практичный алгоритм фильтрации приводит к быстрому вейвлету преобразованию - кубу, в которую проходит сигнал, и из которого быстро выходят вейвлеты коэффициенты. Давайте рассмотрим это более подробно.
Для многих сигналов низкочастотное содержимое является самой важной частью. Это то, что придает сигналу свои тождества. Высокочастотное содержимое, с другой стороны, придает аромат или нюанс. Рассмотрим человеческий голос. Если вы удаляете высокочастотные компоненты, голос звучит по-другому, но вы все еще можете сказать, что говорится. Однако, если вы удаляете достаточно низкочастотных компонентов, вы слышите гиббериш.
В вейвлет мы часто говорим о приближениях и деталях. Приближения являются высокомасштабными низкочастотными компонентами сигнала. Детали - низкомасштабные высокочастотные компоненты.
Процесс фильтрации на самом базовом уровне выглядит так.
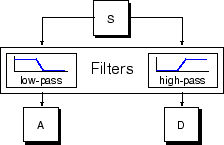
Исходный сигнал, S, проходит через два дополнительных фильтра и появляется как два сигнала.
К сожалению, если мы действительно выполняем эту операцию по реальному цифровому сигналу, мы получаем в два раза больше данных, чем начали. Предположим, например, что исходный сигнал S состоит из 1000 выборок данных. Затем получившиеся сигналы будут иметь 1000 выборок каждый, в общей сложности 2000.
Эти сигналы A и D интересны, но мы получаем 2000 значений вместо 1000, которые у нас были. Существует более тонкий способ выполнить разложение с помощью вейвлетов. Внимательно посмотрев на расчеты, мы можем сохранить только одну точку из двух в каждой из двух выборок 2000-й длины, чтобы получить полную информацию. Это понятие понижающей дискретизации. Мы производим две последовательности, называемые cA и cD.
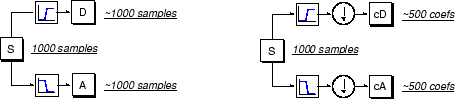
Процесс справа, который включает понижающую дискретизацию, создает коэффициенты DWT.
Чтобы лучше оценить этот процесс, давайте выполним одностадийное дискретное вейвлет сигнала. Наш сигнал будет чистой синусоидой с добавлением высокочастотного шума.
Вот наша принципиальная схема с вставленными в нее реальными сигналами.
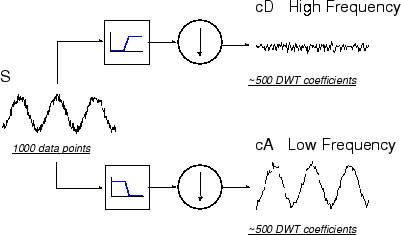
MATLAB® код, необходимый для генерации s, cD, и cA является
s = sin(20.*linspace(0,pi,1000)) + 0.5.*rand(1,1000); [cA,cD] = dwt(s,'db2');
где db2 - имя вейвлета, который мы хотим использовать для анализа.
Заметьте, что коэффициенты детализации cD малы и состоят в основном из высокочастотного шума, в то время как коэффициенты приближения cA содержат гораздо меньше шума, чем исходный сигнал.
[length(cA) length(cD)] ans = 501 501
Можно заметить, что фактические длины векторов детализации и коэффициента приближения немного больше половины длины исходного сигнала. Это связано с процессом фильтрации, который реализован путем свертки сигнала фильтром. Свертка «мазает» сигнал, вводя в результат несколько дополнительных выборок.
Процесс разложения может быть итерацией, с последовательными приближениями, разлагающимися в свою очередь, так что один сигнал разбивается на многие компоненты более низкого разрешения. Это называется деревом разложения вейвлет.
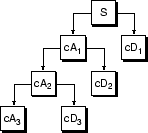
Просмотр дерева вейвлет сигнала может дать ценную информацию.
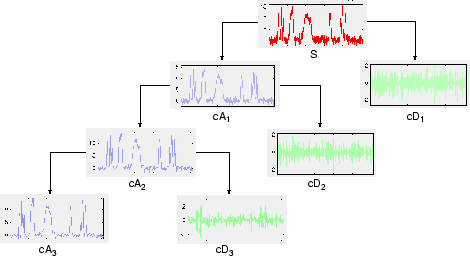
Поскольку процесс анализа является итеративным, в теории он может быть продолжен бесконечно. В действительности разложение может продолжаться только до тех пор, пока отдельные детали не состоят из одной выборки или пикселя. На практике вы выберете подходящее количество уровней на основе характера сигнала или по подходящему критерию, такому как энтропия (см. «Выбор оптимального разложения» в Руководстве пользователя Wavelet Toolbox).