Представление сигнала в конкретном базисе включает нахождение уникального набора коэффициентов расширения в этом базисе. Хотя существует много преимуществ для представления сигнала в базисе, в частности, ортогональном базисе, существуют также недостатки.
Способность базиса обеспечивать разреженное представление зависит от того, насколько хорошо характеристики сигнала соответствуют характеристикам базовых векторов. Для примера сглаженные непрерывные сигналы слабо представлены в базисе Фурье, в то время как импульсы неизвестны. Сглаженный сигнал с изолированными разрывами слабо представлен в вейвлет базисе. Однако вейвлет базиса неэффективен в представлении сигнала, чье преобразование Фурье имеет узкую поддержку высоких частот.
Реальные сигналы часто содержат функции, которые запрещают разреженное представление в любом едином базисе. Для этих сигналов вы хотите возможность выбирать векторы из множества, не ограниченного одним базисом. Поскольку вы хотите убедиться, что можете представлять каждый вектор в пространстве, словарь векторов, из которых вы выбираете, должен охватывать пространство. Однако, поскольку набор не ограничивается одним базисом, словарь не является линейно независимым.
Поскольку векторы в словаре не являются линейно независимым множеством, представление сигнала в словаре не является уникальным. Однако, создав избыточный словарь, можно расширить свой сигнал в наборе векторов, которые адаптируются к временным частотным или временным характеристикам вашего сигнала. Вы можете свободно создавать словарь, состоящий из объединения нескольких основ. Для примера можно сформировать основание для пространства квадратно-интегрируемых функций, состоящих из вейвлета пакетного базиса и локального косинусоидного базиса. Вейвлет базиса пакета хорошо адаптирована к сигналам с различным поведением в различных частотных интервалах. Локальный базис косинуса хорошо адаптирован к сигналам с различным поведением в различных временных интервалах. Способность выбирать векторы из каждой из этих основ значительно увеличивает вашу способность редко представлять сигналы с меняющимися характеристиками.
Определите словарь как набор элементарных базовых блоков с единичной нормой для вашего пространства сигналов. Эти векторы с единичной нормой называются атомами. Если атомы словаря охватывают все пространство сигналов, словарь завершен.
Если атомы словаря образуют линейно-зависимый набор, словарь является избыточным. В большинстве приложений поиска соответствия словарь является полным и избыточным.
Позвольте {, k} обозначить атомы словаря. Предположим, что словарь полон и избыточен. Нет уникального способа представить сигнал из пространства как линейную комбинацию атомов.
Важный вопрос заключается в том, существует ли наилучший способ. Интуитивно удовлетворяющий способ выбора наилучшего представления - это выбор, который с сигналом дает самые большие скалярные произведения (в абсолютном значении). Для примера, лучший сингл
который для атома единичной нормы является величиной скалярной проекции на подпространство, простираемое на
Центральной задачей в сопоставлении преследования является то, как вы выбираете оптимальное M -термовое расширение своего сигнала в словаре .
Предположим, что, словарь атомов обозначается как матрица N на M с M > N. Если полный, избыточный словарь образует систему координат для пространства сигналов, можно получить вектор коэффициента расширения минимальной L2 нормы при помощи оператора системы координат.
Однако вектор коэффициентов, возвращенный оператором системы координат, не сохраняет разреженность. Если сигнал разрежен в словаре, коэффициенты расширения, полученные с помощью оператора канонической системы координат, обычно не отражают эту разреженность. Разреженность вашего сигнала в словаре является признаком, который вы обычно хотите сохранить. Соответствие преследованию адресует сохранение разреженности непосредственно.
Matching pursuit является жадным алгоритмом, который вычисляет лучшее нелинейное приближение к сигналу в полном, избыточном словаре. Совпадающее преследование создает последовательность разреженных приближений к сигналу пошагово. Позвольте Φ = {φk}, обозначают словарь атомов нормы модуля. Позволь f быть твоим сигналом.
Начните, определив R0f = f
Начните поиск соответствия, выбрав атом из словаря, который максимизирует абсолютное значение скалярного произведения с R0f = f. Обозначить атом как
Сформируйте невязку R1f путем вычитания ортогональной проекции R0f в пространство, охватываемое
Итерация путем повторения шагов 2 и 3 на невязке.
Остановите алгоритм, когда вы достигнете некоторого заданного критерия остановки.
В неортогональном (или основном) совпадающем поиске атомы словаря не являются взаимно ортогональными векторами. Поэтому вычитание последующих невязок из предыдущего может ввести компоненты, которые не ортогональны диапазону ранее включенных атомов.
Чтобы проиллюстрировать это, рассмотрим следующий пример. Пример не предназначен для представления рабочего совпадающего алгоритма преследования.
Рассмотрим следующий словарь для евклидова 2-пространства. Этот словарь является системой координат равной нормы.
Предположим, что у вас есть следующий сигнал.
Следующий рисунок иллюстрирует этот пример. Атомы словаря имеют красный цвет. Вектор сигнала в синем цвете.
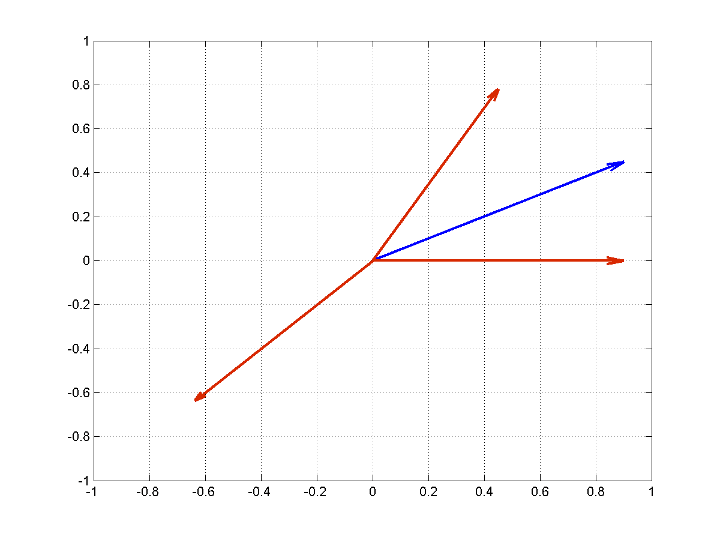
Создайте этот словарь и сигнал в MATLAB®.
dictionary = [1 0; 1/2 sqrt(3)/2; -1/sqrt(2) -1/sqrt(2)]'; x = [1 1/2]';
Вычислите внутренние (скалярные) продукты между атомами сигнала и словаря.
scalarproducts = dictionary'*x;
Самый большой скалярный продукт по абсолютному значению происходит между сигналом и [-1/sqrt(2); -1/sqrt(2)]. Это ясно, потому что угол между этими двумя векторами почти и равен
Сформируйте невязку путем вычитания ортогональной проекции сигнала на [-1/sqrt(2); -1/sqrt(2)] от сигнала. Затем вычислите скалярные произведения остаточного (нового сигнала) с оставшимися атомами словаря. Не обязательно включать [-1/sqrt(2); -1/sqrt(2)] потому что невязка ортогональна этому вектору по конструкции.
residual = x-scalarproducts(3)*dictionary(:,3); scalarproducts = dictionary(:,1:2)'*residual;
Самый большой скалярный продукт по абсолютному значению получен с [1;0]. Лучшими двумя атомами в словаре из двух итераций являются [-1/sqrt(2); -1/sqrt(2)] и [1;0]. Если вы итератируете невязку, вы видите, что выход больше не ортогональен выбранному первому атому. Другими словами, алгоритм ввел компонент, который не ортогональен диапазону выбранного первого атома. Этот факт и связанные с ним осложнения со сходимостью аргументируют в пользу ортогонального совпадения преследования (OMP).
В ортогональном поиске соответствия (OMP), невязка всегда ортогональен диапазону уже выбранных атомов. Это приводит к сходимости для d -мерного вектора после наиболее d шагов .
Концептуально можно сделать это с помощью Грама-Шмидта, чтобы создать ортонормальный набор атомов. С ортонормальным набором атомов вы видите, что для d -мерного вектора можно найти самое d ортогональные направления.
Алгоритм OMP:
Обозначите свой сигнал по f. Инициализируйте невязку R0f = f.
Выберите атом, который максимизирует абсолютное значение скалярного произведения с R0f = f. Обозначить атом как
Сформируйте матрицу, Φ, с ранее выбранными атомами в качестве столбцов. Задайте оператор ортогональной проекции на диапазон столбцов Φ.
Примените оператор ортогональной проекции к невязке.
Обновите невязку.
I - матрица тождеств.
Ортогональное совпадение обеспечивает, чтобы компоненты в диапазоне ранее выбранных атомов не вводились на последующих стадиях.
Может быть в вычислительном отношении эффективным ослабить критерий, что выбранный атом максимизирует абсолютное значение скалярного произведения до менее строгого.
Это известно как слабое совпадение преследования.