Документация

Вейвлет Данных сжатие

Характеристики сжатия данного вейвлет-базиса в основном связаны с относительной трудностью представления вейвлет-области для сигнала. Понятие, лежащее в основе сжатия, основано на концепции, что правильный компонент сигнала может быть точно аппроксимирована с помощью следующих элементов: небольшого количества коэффициентов приближения (на подходящем выбранном уровне) и некоторых коэффициентов детализации.

Как и шумоподавление, процедура сжатия содержит три шага:

Различие процедуры шумоподавления обнаружено на этапе 2. Существует два подхода к сжатию. Первый состоит из взятия вейвлет сигнала и сохранения наибольших коэффициентов абсолютного значения. В этом случае можно задать глобальный порог, эффективность сжатия или относительную квадратную норму эффективности восстановления.

Таким образом, необходимо выбрать только один параметр. Второй подход состоит в применении визуально определенных зависящих от уровня порогов.

Давайте рассмотрим два реальных примера сжатия с использованием глобального порога для данного и неоптимизированного выбора вейвлета, чтобы получить почти полное восстановление квадратной нормы для сигнала (см. «Сжатие сигнала») и для изображения (см. «Сжатие изображения»).

% Load electrical signal and select a part. 
load leleccum; indx = 2600:3100; 
x = leleccum(indx);
% Perform wavelet decomposition of the signal. 
n = 3; w = 'db3'; 
[c,l] = wavedec(x,n,w);
% Compress using a fixed threshold. 
thr = 35; 
keepapp = 1;
[xd,cxd,lxd,perf0,perfl2] = ...
   wdencmp('gbl',c,l,w,n,thr,'h',keepapp);

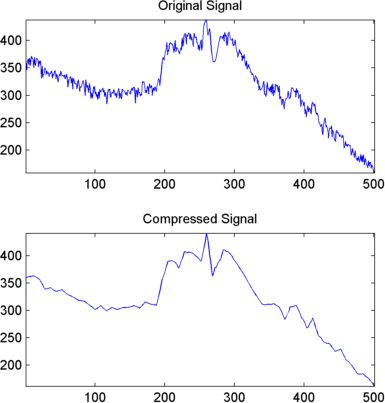
Результат вполне удовлетворителен не только из-за критерия восстановления нормы, но и на визуальной точке зрения восприятия. При реконструкции используется только 15% коэффициентов.

% Load original image. 
load woman; x = X(100:200,100:200); 
nbc = size(map,1);

% Wavelet decomposition of x. 
n = 5; w = 'sym2'; [c,l] = wavedec2(x,n,w);

% Wavelet coefficients thresholding. 
thr = 20; 
keepapp = 1;
[xd,cxd,lxd,perf0,perfl2] = ...
                 wdencmp('gbl',c,l,w,n,thr,'h',keepapp);

Если представление вейвлета слишком плотно, аналогичные стратегии могут использоваться в среде вейвлет-пакета, чтобы получить более разреженное представление. Затем можно определить лучшее разложение относительно подходящим образом выбранного энтропийоподобного критерия, который соответствует выбранной цели (шумоподавление или сжатие).