Документация

Что такое стохастический процесс?

Временные ряды _yt являются набором наблюдений относительно переменной, индексированной последовательно по нескольким моментам времени t = 1, 2..., T. Наблюдения временных рядов y ₁, y ₂..., _yT по сути зависит. С точки зрения статистического моделирования это означает, что неуместно обработать временные ряды как случайную выборку независимых наблюдений.

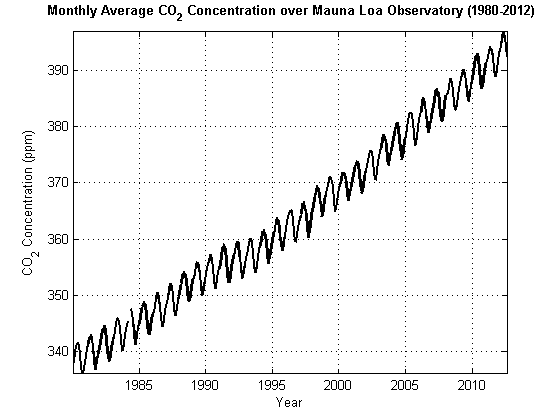
Цель статистического моделирования находит компактное представление генерирующего данные процесса для ваших данных. Статистический базовый блок эконометрического моделирования временных рядов является стохастическим процессом. Эвристическим образом stochastic process является объединенным вероятностным распределением для набора случайных переменных. Путем моделирования наблюдаемых временных рядов _yt как реализация от стохастического процесса $$y=\left\{y_t;t=1,\mathrm{...},T\right\}$$, возможно вместить высоко-размерную и зависимую природу данных. Набор времен наблюдения T может быть дискретным или непрерывным. Рисунок 1-1, Ежемесячный Средний CO2 отображает ежемесячную среднюю концентрацию _CO2 (ppm) зарегистрированный Обсерваторией Мауна-Лоа на Гавайях от 1 980 до 2012 [3].

Стационарные процессы

Стохастическими процессами является weakly stationary или covariance stationary (или просто, stationary), если их первые два момента являются конечными и постоянными в зависимости от времени. А именно, если _yt является стационарным стохастическим процессом, то для всего t:

График вашего стохастического процесса, кажется, увеличиваются или уменьшаются без связанного? Ответ на этот вопрос указывает, является ли стохастический процесс стационарным. “Да” указывает, что стохастический процесс может быть неустановившимся. В рисунке 1-1, Ежемесячном Среднем CO2, концентрация _CO2 увеличивается без связанного, который указывает на неустановившийся стохастический процесс.

Линейная модель временных рядов

Теорема пустоши [2] состояния, что можно написать все слабо стационарные стохастические процессы в общей линейной форме

Здесь, $${\epsilon }_t$$ обозначает последовательность некоррелированых (но не обязательно независимый) случайные переменные от четко определенного вероятностного распределения со средним нулем. Это часто называется innovation process, потому что это получает всю новую информацию в системе во время t.

Модульный корневой процесс

Линейной моделью временных рядов является unit root process, если набор решения к его характеристическому уравнению содержит корень, который находится на модульном круге (i.e., имеет абсолютное значение одного). Впоследствии, ожидаемое значение, отклонение или ковариация элементов стохастического процесса растут со временем, и поэтому являются неустановившимися. Если ваш ряд имеет модульный корень, то дифференцирование он может сделать его стационарным.

Например, рассмотрите линейную модель временных рядов $$y_t=y_{t-1}+{\epsilon }_t,$$ где $${\epsilon }_t$$ последовательность белого шума инноваций с отклонением σ² (это называется случайным обходом). Характеристическое уравнение этой модели $$z-1=0,$$ который имеет корень одного. Если начальное наблюдение_{, y0} фиксируется, то можно записать модель как $$y_t=y_0+{\displaystyle \sum _{i=1}^t{\epsilon }_i}.$$ Его ожидаемым значением является _y0, который независим от времени. Однако отклонение ряда является tσ², который растет со временем, делая ряд нестабильным. Возьмите первое различие, чтобы преобразовать ряд, и модель становится $$d_t=y_t-y_{t-1}={\epsilon }_t$$. Характеристическое уравнение для этого ряда $$z=0$$, таким образом, это не имеет модульного корня. Обратите внимание на то, что

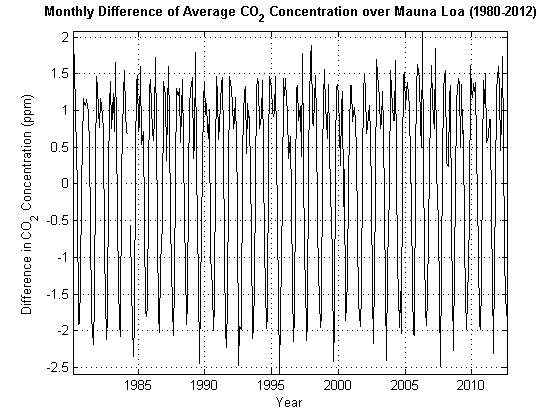
Рисунок 1-1, Ежемесячный Средний CO2 кажется неустановившимся. Что происходит, если вы строите первое различие _dt = _{yt – y  t –1} из этого ряда? Рисунок 1-2, Ежемесячное Различие в CO2 отображает _dt. Игнорируя колебания, стохастический процесс, кажется, не увеличивается или не уменьшается в целом. Можно прийти к заключению, что _dt является стационарным, и что _yt является модульным неустановившимся корнем. Для получения дополнительной информации смотрите Дифференцирование.

Изолируйте обозначение оператора

L lag operator управляет на временных рядах _yt, таким образом что $$L^i{y}_t=y_{t-i}$$.

Th-степень m изолирует полином коэффициентов b ₁, b ₂..., _bm задан как

В обозначении оператора задержки можно записать общую линейную модель с помощью полинома бесконечной степени $$\psi (L)=(1+{\psi }_{1}L+{\psi }_2{L}^2+\dots ),$$

Вы не можете оценить модель, которая имеет полином бесконечной степени коэффициентов с конечным объемом данных. Однако, если $$\psi (L)$$ рациональный полином (или приблизительно рациональный), можно записать его (по крайней мере, приблизительно) как частное двух полиномов конечной степени.

Задайте q - полином степени $$\theta (L)=(1+{\theta }_{1}L+{\theta }_2{L}^2+\dots +{\theta }_q{L}^q)$$ и p - полином степени $$\varphi (L)=(1+{\varphi }_{1}L+{\varphi }_2{L}^2+\dots +{\varphi }_p{L}^p)$$. Если $$\psi (L)$$ рационально, затем

Таким образом, теоремой Пустоши, можно смоделировать (или тесно аппроксимировать), каждый стационарный стохастический процесс как

который имеет p + коэффициенты q (конечное число).

Характеристическое уравнение

Степень p characteristic polynomial линейной модели временных рядов $$y_t={\varphi }_1{y}_{t-1}+{\varphi }_2{y}_{t-2}+\mathrm{...}+{\varphi }_p{y}_{t-p}+{\epsilon }_t$$

Это - другой способ оценить это, ряд является стационарным процессом. Например, характеристическое уравнение $$y_t=0.5y_{t-1}-0.02y_{t-2}+{\epsilon }_t$$ $$\varphi (a)=a^2-0.5a+\mathrm{0.02.}$$

Корни homogeneous characteristic equation $$\varphi (a)=0$$ (названный characteristic roots), определяют, являются ли линейные временные ряды стационарными. Если каждый корень в $$\varphi (a)$$ находится в модульном кругу, затем процесс является стационарным. Корни лежат в модульном кругу, если у них есть абсолютное значение меньше чем один. Это - модульный корневой процесс, если один или несколько корней лежат в модульном кругу (i.e., имейте абсолютное значение одного). Продолжая пример, характеристические корни $$\varphi (a)=0$$ $$a=\{0.4562,0.0438\}.$$ Поскольку абсолютные значения этих корней меньше один, линейная модель временных рядов является стационарной.