Следующая диагностика оценки и симуляции

Эмпирические, пользовательские, и полусопряженные предшествующие модели дают к аналитически тяжелым апостериорным распределениям (для получения дополнительной информации, смотрите Аналитически Тяжелое Последующее поколение). Чтобы обобщить апостериорное распределение для оценки и вывода, первая модель требует выборки Монте-Карло, в то время как последние две модели требуют выборки Цепи Маркова Монте-Карло (MCMC). При оценке последующего поколения, использующего выборку Монте-Карло, особенно выборку MCMC, можно столкнуться с проблемами, приводящими к выборкам, которые неверно представляют или не обобщают апостериорное распределение. В этом случае оценки и выводы на основе следующих ничьих могут быть неправильными.

Даже если следующее аналитически послушно, или ваша выборка MCMC представляет истину, следующую хорошо, ваш выбор предшествующего распределения может влиять на апостериорное распределение нежелательными способами. Например, небольшое изменение предшествующего распределения, такого как маленькое увеличение значения предшествующего гиперпараметра, может оказать большое влияние на следующие оценки или выводы. Если следующее настолько чувствительно к предшествующим предположениям, то интерпретации статистики и выводов на основе следующей силы вводят в заблуждение.

Поэтому после получения апостериорного распределения из алгоритма выборки, важно определить качество выборки. Кроме того, независимо от того, послушно ли следующее аналитически, важно проверять, насколько чувствительный следующее к предшествующим предположениям распределения.

Диагностируйте выборки MCMC

При рисовании выборки MCMC хорошая практика должна чертить меньшую, экспериментальную выборку, и затем представление trace plots чертивших значений параметров, чтобы проверять, соответствует ли выборка. Trace plots является графиками чертивших значений параметров относительно индекса симуляции. Удовлетворительная выборка MCMC достигает стационарного распределения быстро и смешивается хорошо, то есть, исследует распределение на широких шагах с мало ни к какой памяти о предыдущей ничьей. Этот рисунок является примером удовлетворительной выборки MCMC.

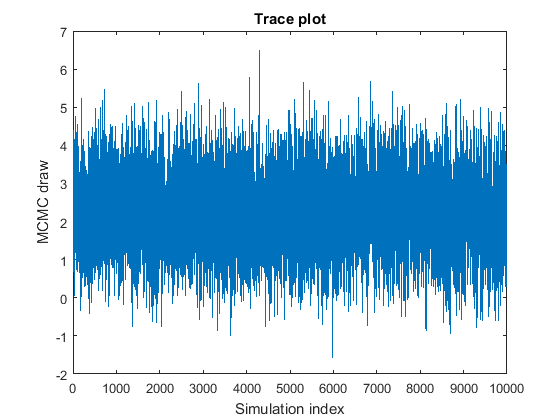
Этот список описывает проблематичные характеристики выборок MCMC, дает пример того, что искать в графике трассировки и описывает, как решить проблему.

Выборка MCMC, кажется, перемещается в стационарное распределение, то есть, это отображает transient behavior.
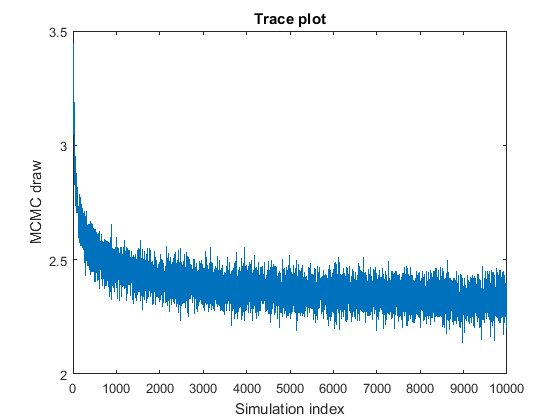
Чтобы исправить проблему, используйте один из следующих методов:
- Задайте начальные значения для параметров, которые ближе к среднему значению стационарного распределения или задают значение, которое вы ожидаете в следующем, с помощью BetaStart и Sigma2Start аргументы в виде пар имя-значение.
- Задайте период burn-in, то есть, номер чертит запуск с начала удалить из следующей оценки, с помощью BurnIn аргумент пары "имя-значение". Электротермотренировка должна быть достаточно большой так, чтобы остающаяся выборка напомнила удовлетворительную выборку MCMC, и достаточно маленький так, чтобы настроенный объем выборки был достаточно большим.
Выборка MCMC отображает высоко последовательную корреляцию. Следующие фигуры являются графиками трассировки и автокорреляционной функцией (ACF) графики (см. autocorr).
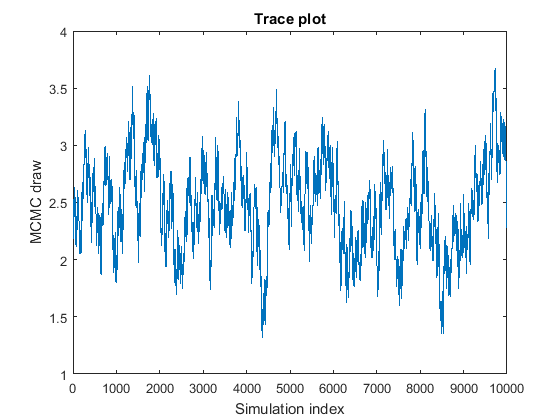
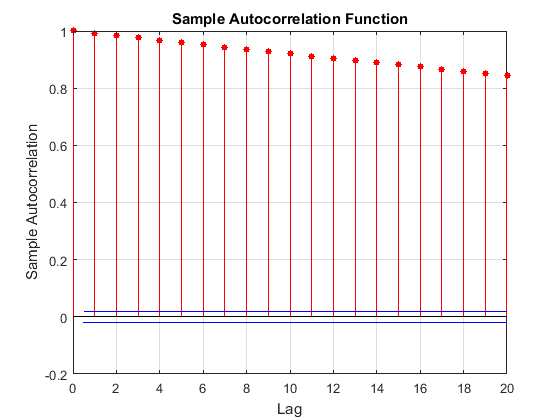
График трассировки показывает, что последующие выборки, кажется, функция прошлых выборок. График ACF показателен из процесса с высокой автокорреляцией.
Такие выборки MCMC смешиваются плохо и занимают много времени, чтобы достаточно исследовать распределение. Попробуйте следующее:
- Если у вас есть достаточно ресурсов, то оценки на основе больших выборок MCMC приблизительно правильны.
- Чтобы уменьшать высокую автокорреляцию, можно сохранить часть выборки MCMC thinning с помощью Thin аргумент пары "имя-значение".
- Для пользовательских предшествующих моделей попробуйте различный сэмплер при помощи 'Sampler' аргумент пары "имя-значение". Чтобы настроить настраивающиеся параметры сэмплера, создайте структуру опций сэмплера вместо этого при помощи sampleroptions, который позволяет вам задавать сэмплер и значения для его настраивающих параметров. Затем передайте структуру опций сэмплера estimate, simulate, или forecast при помощи 'Options' аргумент пары "имя-значение".
Выборка MCMC переходит в зависимости от государства.
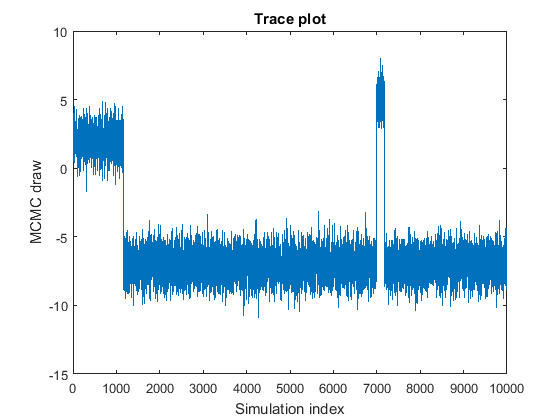
График показывает подвыборки, сосредоточенные в значениях 2, –7, и 5, которые смешиваются хорошо. Это поведение может указать на одно из следующих качеств:
- По крайней мере один из параметров не идентифицируется. Вам придется преобразовать вашу модель и предположения.
- Там может кодировать проблемы с вашим сэмплером Гиббса.
- Стационарное распределение многомодально. В этом примере, вероятности того, чтобы быть в состоянии, сосредоточенном в –7 является самым высоким, сопровождается 2, и затем 5. Вероятность перемещения из состояния, сосредоточенного в 7 является низким.
  Если ваше предшествующее сильно, и ваш объем выборки мал, то вы можете видеть этот тип выборки MCMC, которая не обязательно проблематична.
Цепь Маркова не сходится к своему стационарному распределению.
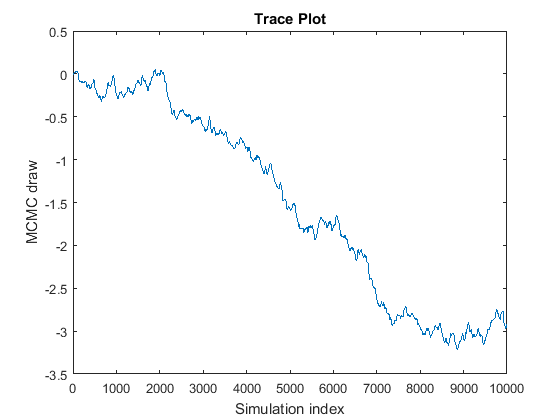
Кривая похожа на случайный обход, потому что MCMC медленно исследует следующее. Если эта проблема происходит, то следующие оценки на основе выборки MCMC являются неправильными. Чтобы исправить проблему, попробуйте следующие методы:
- Если вы имеете достаточно ресурсов, чертите намного больше выборок, и затем определяете, обосновывается ли цепь в конечном счете и незначительно смешивается. Если это действительно обосновывается и смешивается относительно хорошо, то удаляет начинающийся фрагмент выборки и рассматривает утончающуюся остальную часть выборки. Например, предположите, что вы чертите 20000 выборки цепи на рисунке, и затем вы находите, что цепь обосновывается вокруг -3 после 7000 чертит. Можно обработать, чертит 1:7000 как выжигание дефектов (BurnIn), и затем тонкий (Thin) остающиеся ничьи, чтобы достигнуть удовлетворительного уровня автокорреляции.
- Повторно параметрируйте предшествующее распределение. При оценке customblm объекты модели, можно задать репараметризацию отклонения воздействия к логарифмической шкале с помощью Reparameterize аргумент пары "имя-значение".
- Для пользовательских предшествующих моделей попробуйте различный сэмплер при помощи 'Sampler' аргумент пары "имя-значение". Чтобы настроить настраивающиеся параметры сэмплера, создайте структуру опций сэмплера вместо этого при помощи sampleroptions, который позволяет вам задавать сэмплер и значения для его настраивающих параметров. Затем передайте структуру опций сэмплера estimate, simulate, или forecast при помощи 'Options' аргумент пары "имя-значение".

Кроме того, прослеживать и графики ACF, estimate, simulate, и forecast оцените effective sample size. Если эффективный объем выборки меньше 1% количества наблюдений, то те функции выдают предупреждения. Для получения дополнительной информации см. [1].

Выполните анализ чувствительности

sensitivity analysis включает определение, как устойчивые следующие оценки к предшествующему и предположениям распределения данных. Таким образом, цель состоит в том, чтобы изучить, как заменяющий начальные значения и предшествующие предположения с разумными альтернативами влияет на апостериорное распределение и выводы. Если следующее и выводы не варьируются очень относительно приложения, то следующее устойчиво к предшествующим предположениям и начальным значениям. Последующее поколение и выводы, которые действительно варьируются существенно с различными начальными предположениями, могут привести к неправильным интерпретациям.

Выполнять анализ чувствительности:

Идентифицируйте набор разумных предшествующих моделей. Включайте рассеянный (diffuseblm) модели и субъективный (conjugateblm или semiconjugateblm) модели, которые легче интерпретировать и позволить включение предшествующей информации.
Для каждой из предшествующих моделей определите набор вероятных гиперзначений параметров. Например, для нормальной обратной гаммы спрягают или полуспрягают предшествующие модели, выбирают различные значения для предшествующей средней и ковариационной матрицы коэффициентов регрессии и формы и масштабных коэффициентов обратного гамма распределения отклонения воздействия. Для получения дополнительной информации смотрите MuVA, и B аргументы пары "имя-значение" bayeslm.
Для всех предшествующих предположений модели:
1. Оцените соответствующее использование последующего поколения estimate.
2. Чертите выводы с помощью следующего. Например, получите 95% equitailed вероятные интервалы или предскажите ответы, данные использование данных о предикторе forecast.
Сравните оценки и выводы среди моделей.
- Если все оценки и выводы достаточно подобны, то следующее устойчиво.
- Если оценки или выводы достаточно отличаются, то может быть некоторая базовая проблема с выбранным уголовным прошлым или вероятностью данных. Поскольку Байесова среда линейной регрессии в Econometrics Toolbox™ всегда принимает, что данные являются Гауссовыми, рассматривают:
  - Добавление или удаление переменных предикторов из модели регрессии
  - Создание более информативного уголовного прошлого
  - Совершенно другие предшествующие предположения

Для получения дополнительной информации об анализе чувствительности см. [2], Ch. 6.

Ссылки

[1] Geyer, C. J. “Практическая Цепь Маркова Монте-Карло”. Статистическая Наука. Издание 7, 1992, стр 473-483.

[2] Джелмен, A., Дж. Б. Карлин, Х. С. Стерн и Д. Б. Рубин. Байесов анализ данных, 2-й. Эд. Бока-Ратон, FL: Chapman & Hall/CRC, 2004.

Смотрите также

estimate | simulate | forecast

Документация