portoptЭтот пример строит границу эффективности гипотетического портфеля трех активов. Это иллюстрирует, как задать ожидаемые доходы, стандартные отклонения и корреляции портфеля активов, как преобразовать стандартные отклонения и корреляции в ковариационную матрицу, и как вычислить и построить границу эффективности от возвратов и ковариационной матрицы. Пример также иллюстрирует, как случайным образом сгенерировать набор весов портфеля, и как добавить случайные портфели в существующий график для сравнения с границей эффективности.
Во-первых, задайте ожидаемые доходы, стандартные отклонения и корреляционную матрицу для гипотетического портфеля трех активов.
Returns = [0.1 0.15 0.12];
STDs = [0.2 0.25 0.18];
Correlations = [ 1 0.3 0.4
0.3 1 0.3
0.4 0.3 1 ];
Преобразуйте стандартные отклонения и корреляционную матрицу в ковариационную матрицу отклонения с функцией corr2cov.
Covariances = corr2cov(STDs, Correlations)
Covariances =
0.0400 0.0150 0.0144
0.0150 0.0625 0.0135
0.0144 0.0135 0.0324Оцените и постройте границу эффективности в 20 точках вдоль границы, с помощью функции portopt и ожидаемые доходы и соответствующая ковариационная матрица. Несмотря на то, что скорее уточняют, ограничения могут быть помещены в активы в портфеле, поскольку простота принимает ограничения по умолчанию и масштабирует итоговое значение портфеля к 1 и ограничивает веса быть положительными (никакая короткая продажа).
Примечание
portopt был частично удален и больше не будет принимать ConSet или varargin аргументы. Используйте Portfolio возразите вместо этого, чтобы решить задачи портфеля, которые являются больше, чем длинно-единственный полностью инвестированный портфель. Для получения информации о рабочем процессе при использовании объектов Портфеля смотрите Рабочий процесс Объекта Портфеля. Для получения дополнительной информации о миграции portopt код к Portfolio, см. portopt Миграцию к Объекту Портфеля.
portopt(Returns, Covariances, 20)
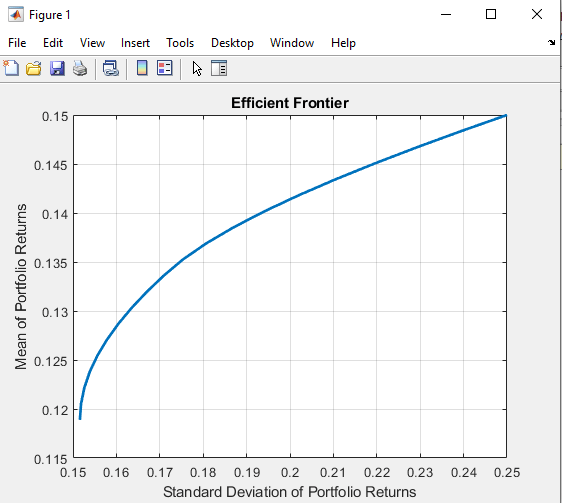
Теперь, когда граница эффективности отображена, случайным образом сгенерируйте веса актива для 1 000 портфелей, начинающих с MATLAB® начальное состояние.
rng('default')
Weights = rand(1000, 3);Предыдущая строка кода генерирует три столбца равномерно распределенных случайных весов, но не гарантирует, что они суммируют к 1. Следующий сегмент кода нормирует веса каждого портфеля так, чтобы общее количество этих трех весов представляло допустимый портфель.
Total = sum(Weights, 2); % Add the weights Total = Total(:,ones(3,1)); % Make size-compatible matrix Weights = Weights./Total; % Normalize so sum = 1
Учитывая 1 000 случайных созданных портфелей, вычислите ожидаемый доход и риск каждого портфеля, сопоставленного с весами.
[PortRisk, PortReturn] = portstats(Returns, Covariances, Weights);
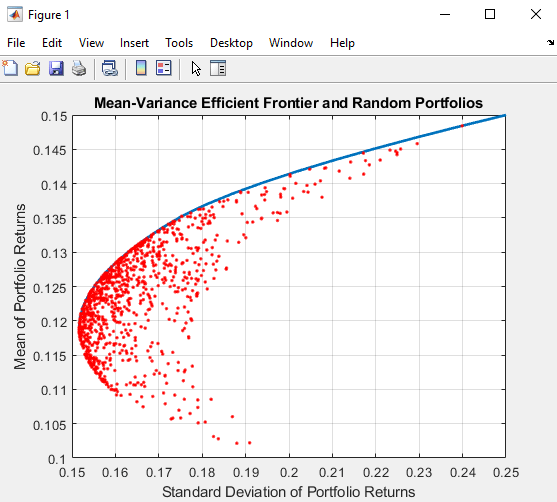
Наконец, содержите текущий график и постройте возвраты и риски каждого портфеля сверх существующей границы эффективности для сравнения. После графического вывода аннотируйте график заголовком и возвратите график в состояние содержания значения по умолчанию (любые последующие графики сотрут существующие данные). Граница эффективности появляется в синем, в то время как 1 000 случайных портфелей появляются в виде набора красных точек на или ниже границы.
hold on plot (PortRisk, PortReturn, '.r') title('Mean-Variance Efficient Frontier and Random Portfolios') hold off
bnddury | bndconvy | bndprice | bndkrdur | blsprice | blsdelta | blsgamma | blsvega | zbtprice | zero2fwd | zero2disc | corr2cov | portopt