quaternion

Создайте массив кватерниона

Описание

Кватернион является гиперкомплексным числом с четырьмя частями, используемым в трехмерных вращениях и ориентациях.

Номер кватерниона представлен в форме $a + b i + c j + d k$ , где a, b, c и части d являются вещественными числами и i, j, и k являются базисными элементами, удовлетворяя уравнению: i² = j² = k² = ijk = −1.

Набор кватернионов, обозначенных H, задан в четырехмерном векторном пространстве по вещественным числам, R⁴. Каждый элемент H имеет уникальное представление на основе линейной комбинации базисных элементов, i, j, и k.

Все вращения в 3-D могут быть описаны осью вращения и угла о той оси. Преимущество кватернионов по матрицам вращения состоит в том, что ось и угол вращения легко интерпретировать. Например, рассмотрите вопрос в R³. Чтобы вращать точку, вы задаете ось вращения и угол вращения.

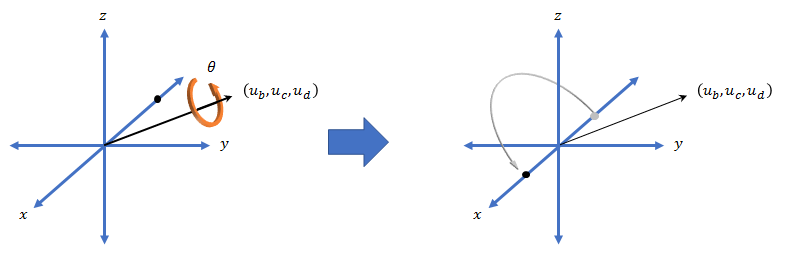
Rotation Illustration

Представление кватерниона вращения может быть описано как $q = \cos (\frac{θ}{2}) + \sin (\frac{θ}{2}) (u_{b} i + u_{c} j + u_{d} k)$ , где θ является углом вращения и [_ub, _uc, и _ud] является осью вращения.

Создание

Синтаксис

quat = quaternion()

quat = quaternion(A,B,C,D)

quat = quaternion(matrix)

quat = quaternion(RV,'rotvec')

quat = quaternion(RV,'rotvecd')

quat = quaternion(RM,'rotmat',PF)

quat = quaternion(E,'euler',RS,PF)

quat = quaternion(E,'eulerd',RS,PF)

Описание

пример

quat = quaternion() создает пустой кватернион.

пример

quat = quaternion(A,B,C,D) создает массив кватерниона, где четыре части кватерниона взяты из массивов ABC, и D. Все входные параметры должны иметь тот же размер и быть совпадающего типа данных.

пример

quat = quaternion(matrix) создает N-by-1 массив кватерниона от N-by-4 матрица, где каждый столбец становится одной частью кватерниона.

пример

quat = quaternion(RV,'rotvec') создает N-by-1 массив кватерниона от N-by-3 матрица векторов вращения, RV. Каждая строка RV представляет вектор вращения в радианах.

пример

quat = quaternion(RV,'rotvecd') создает N-by-1 массив кватерниона от N-by-3 матрица векторов вращения, RV. Каждая строка RV представляет вектор вращения в градусах.

пример

quat = quaternion(RM,'rotmat',PF) создает N-by-1 массив кватерниона от 3 3 N массивом матриц вращения, RM. PF может быть любой 'point' если Углы Эйлера представляют вращения точки или 'frame' для вращений системы координат.

пример

quat = quaternion(E,'euler',RS,PF) создает N-by-1 массив кватерниона от N-by-3 матрица, E. Каждая строка E представляет набор Углов Эйлера в радианах. Углы в E вращения вокруг осей в последовательности RS.

пример

quat = quaternion(E,'eulerd',RS,PF) создает N-by-1 массив кватерниона от N-by-3 матрица, E. Каждая строка E представляет набор Углов Эйлера в градусах. Углы в E вращения вокруг осей в последовательности RS.

Входные параметры

развернуть все

`A,B,C,D` — Части кватерниона
разделенные от запятой массивы, одного размера

Части кватерниона в виде четырех разделенных от запятой скаляров, матриц или многомерных массивов, одного размера.

Пример: quat = quaternion(1,2,3,4) создает кватернион формы 1 + 2i + 3j + 4k.

Пример: quat = quaternion([1,5],[2,6],[3,7],[4,8]) создает 1 2 массив кватерниона где quat(1,1) = 1 + 2i + 3j + 4k и quat(1,2) = 5 + 6i + 7j + 8k

Типы данных: single | double

`matrix` — Матрица частей кватерниона
N-by-4 матрица

Матрица частей кватерниона в виде N-by-4 матрица. Каждая строка представляет отдельный кватернион. Каждый столбец представляет отдельную часть кватерниона.

Пример: quat = quaternion(rand(10,4)) создает массив кватерниона 10 на 1.

Типы данных: single | double

`RV` — Матрица векторов вращения
N-by-3 матрица

Матрица векторов вращения в виде N-by-3 матрица. Каждая строка RV представляет [X Y Z] элементы вектора вращения. Вектор вращения является единичным вектором, представляющим ось вращения, масштабируемого углом вращения в радианах или степенях.

Чтобы использовать этот синтаксис, задайте первый аргумент как матрицу векторов вращения и второго аргумента как 'rotvec' или 'rotvecd'.

Пример: quat = quaternion(rand(10,3),'rotvec') создает массив кватерниона 10 на 1.

Типы данных: single | double

`RM` — Матрицы вращения
3х3 матрица | 3 3 N массивом

Массив матриц вращения, заданных 3х3 матрицей или 3 3 N массивом. Каждая страница массива представляет отдельную матрицу вращения.

Пример: quat = кватернион (rand (3), 'rotmat', 'точка')

Пример: quat = кватернион (rand (3), 'rotmat', 'система координат')

Типы данных: single | double

`PF` — Тип матрицы вращения
`'point'` | `'frame'`

Тип матрицы вращения, заданной 'point' или 'frame'.

Пример: quat = кватернион (rand (3), 'rotmat', 'точка')

Пример: quat = кватернион (rand (3), 'rotmat', 'система координат')

Типы данных: char | string

`E` — Матрица Углов Эйлера
N-by-3 матрица

Матрица Углов Эйлера, заданных N-by-3 матрица. При использовании 'euler' синтаксис, задайте E в радианах. При использовании 'eulerd' синтаксис, задайте E в градусах.

Пример: quat = кватернион (E, 'Эйлер', 'YZY', 'точка')

Пример: quat = кватернион (E, 'Эйлер', 'XYZ', 'система координат')

Типы данных: single | double

`RS` — Последовательность вращения
вектор символов | скалярная строка

Последовательность вращения в виде трехэлементного вектора символов:

'YZY'
'YXY'
'ZYZ'
'ZXZ'
'XYX'
'XZX'
'XYZ'
'YZX'
'ZXY'
'XZY'
'ZYX'
'YXZ'

Примите, что вы хотите определить новые координаты точки, когда ее система координат вращается с помощью вращения системы координат. Точка задана в системе исходной координаты как:

point = [sqrt(2)/2,sqrt(2)/2,0];

В этом представлении первый столбец представляет x - ось, второй столбец представляет y - ось, и третий столбец представляет z - ось.

Вы хотите вращать точку с помощью представления Угла Эйлера [45,45,0]. Вращайте точку с помощью двух различных последовательностей вращения:

Если вы создаете вращающее устройство кватерниона и задаете последовательность 'ZYX', система координат сначала вращается 45 ° вокруг z - ось, то 45 ° вокруг нового y - ось.
```
quatRotator = quaternion([45,45,0],'eulerd','ZYX','frame');
newPointCoordinate = rotateframe(quatRotator,point)
```
```
newPointCoordinate =

    0.7071   -0.0000    0.7071
```
Если вы создаете вращающее устройство кватерниона и задаете последовательность 'YZX', система координат сначала вращается 45 ° вокруг y - ось, то 45 ° вокруг нового z - ось.
```
quatRotator = quaternion([45,45,0],'eulerd','YZX','frame');
newPointCoordinate = rotateframe(quatRotator,point)
```
```
newPointCoordinate =

    0.8536    0.1464    0.5000
```

Типы данных: char | string

Функции объекта

`angvel`	Скорость вращения от массива кватерниона
`classUnderlying`	Класс частей в кватернионе
`compact`	Преобразуйте массив кватерниона в N-by-4 матрица
`conj`	Сопряженное комплексное число кватерниона
`'`	Комплексное сопряженное транспонирование массива кватерниона
`dist`	Угловое расстояние в радианах
`euler`	Преобразуйте кватернион в Углы Эйлера (радианы)
`eulerd`	Преобразуйте кватернион в Углы Эйлера (степени)
`exp`	Экспоненциал массива кватерниона
`.\,ldivide`	Поэлементное левое деление кватерниона
`log`	Натуральный логарифм массива кватерниона
`meanrot`	Среднее вращение кватерниона
`-`	Вычитание кватерниона
`*`	Умножение кватерниона
`norm`	Норма кватерниона
`normalize`	Нормализация кватерниона
`ones`	Создайте массив кватерниона с набором действительных частей одному и обнуленным мнимым частям
`parts`	Извлеките части кватерниона
`.^,power`	Поэлементная степень кватерниона
`prod`	Продукт массива кватерниона
`randrot`	Равномерно распределенные случайные вращения
`./,rdivide`	Поэлементное правое деление кватерниона
`rotateframe`	Вращение системы координат кватерниона
`rotatepoint`	Вращение точки кватерниона
`rotmat`	Преобразуйте кватернион в матрицу вращения
`rotvec`	Преобразуйте кватернион в вектор вращения (радианы)
`rotvecd`	Преобразуйте кватернион в вектор вращения (в градусах)
`slerp`	Сферическая линейная интерполяция
`.*,times`	Поэлементное умножение кватерниона
`'`	Транспонируйте массив кватерниона
`-`	Кватернион, унарный минус
`zeros`	Создайте массив кватерниона со всеми обнуленными частями

Примеры

свернуть все

Создайте пустой кватернион

Скрипт Open Live Script

quat = quaternion()

quat = 

  0x0 empty quaternion array

По умолчанию базовый класс кватерниона является двойным.

classUnderlying(quat)

ans = 
'double'

Создайте кватернион путем определения отдельных частей кватерниона

Скрипт Open Live Script

Можно создать массив кватерниона путем определения этих четырех частей как разделенных запятой скаляров, матриц или многомерных массивов, одного размера.

Задайте части кватерниона как скаляры.

A = 1.1;
B = 2.1;
C = 3.1;
D = 4.1;
quatScalar = quaternion(A,B,C,D)

quatScalar = quaternion
     1.1 + 2.1i + 3.1j + 4.1k

Задайте части кватерниона как вектор-столбцы.

A = [1.1;1.2];
B = [2.1;2.2];
C = [3.1;3.2];
D = [4.1;4.2];
quatVector = quaternion(A,B,C,D)

quatVector = 2x1 quaternion array
     1.1 + 2.1i + 3.1j + 4.1k
     1.2 + 2.2i + 3.2j + 4.2k

Задайте части кватерниона как матрицы.

A = [1.1,1.3; ...
     1.2,1.4];
B = [2.1,2.3; ...
     2.2,2.4];
C = [3.1,3.3; ...
     3.2,3.4];
D = [4.1,4.3; ...
     4.2,4.4];
quatMatrix = quaternion(A,B,C,D)

quatMatrix = 2x2 quaternion array
     1.1 + 2.1i + 3.1j + 4.1k     1.3 + 2.3i + 3.3j + 4.3k
     1.2 + 2.2i + 3.2j + 4.2k     1.4 + 2.4i + 3.4j + 4.4k

Задайте части кватерниона как трехмерные массивы.

A = randn(2,2,2);
B = zeros(2,2,2);
C = zeros(2,2,2);
D = zeros(2,2,2);
quatMultiDimArray = quaternion(A,B,C,D)

quatMultiDimArray = 2x2x2 quaternion array
quatMultiDimArray(:,:,1) = 

     0.53767 +       0i +       0j +       0k     -2.2588 +       0i +       0j +       0k
      1.8339 +       0i +       0j +       0k     0.86217 +       0i +       0j +       0k


quatMultiDimArray(:,:,2) = 

     0.31877 +       0i +       0j +       0k    -0.43359 +       0i +       0j +       0k
     -1.3077 +       0i +       0j +       0k     0.34262 +       0i +       0j +       0k

Создайте кватернион путем определения матрицы частей кватерниона

Скрипт Open Live Script

Можно создать скаляр, или вектор-столбец кватернионов задают матрицу N-4 частей кватерниона, где столбцы соответствуют частям A кватерниона, B, C, и D.

Создайте вектор-столбец случайных кватернионов.

quatParts = rand(3,4)

quatParts = 3×4

    0.8147    0.9134    0.2785    0.9649
    0.9058    0.6324    0.5469    0.1576
    0.1270    0.0975    0.9575    0.9706

quat = quaternion(quatParts)

quat = 3x1 quaternion array
     0.81472 + 0.91338i +  0.2785j + 0.96489k
     0.90579 + 0.63236i + 0.54688j + 0.15761k
     0.12699 + 0.09754i + 0.95751j + 0.97059k

Получать quatParts матрица от представления кватерниона, используйте compact.

retrievedquatParts = compact(quat)

retrievedquatParts = 3×4

    0.8147    0.9134    0.2785    0.9649
    0.9058    0.6324    0.5469    0.1576
    0.1270    0.0975    0.9575    0.9706

Создайте кватернион путем определения векторов вращения

Скрипт Open Live Script

Можно создать массив кватерниона N-1 путем определения матрицы N-3 векторов вращения в радианах или степенях. Векторы вращения являются компактными пространственными представлениями, которые имеют непосредственное отношение с нормированными кватернионами.

Векторы вращения в радианах

Создайте скалярный кватернион с помощью вектора вращения и проверьте, что получившийся кватернион нормирован.

rotationVector = [0.3491,0.6283,0.3491];
quat = quaternion(rotationVector,'rotvec')

quat = quaternion
     0.92124 + 0.16994i + 0.30586j + 0.16994k

norm(quat)

ans = 1.0000

Можно преобразовать от кватернионов до векторов вращения в радианах с помощью rotvec функция. Восстановите rotationVector от кватерниона, quat.

rotvec(quat)

ans = 1×3

    0.3491    0.6283    0.3491

Векторы вращения в градусах

rotationVector = [20,36,20];
quat = quaternion(rotationVector,'rotvecd')

quat = quaternion
     0.92125 + 0.16993i + 0.30587j + 0.16993k

norm(quat)

ans = 1

Можно преобразовать от кватернионов до векторов вращения в градусах с помощью rotvecd функция. Восстановите rotationVector от кватерниона, quat.

rotvecd(quat)

ans = 1×3

   20.0000   36.0000   20.0000

Создайте кватернион путем определения матриц вращения

Скрипт Open Live Script

Можно создать массив кватерниона N-1 путем определения 3 3 N массивом матриц вращения. Каждая страница матричного массива вращения соответствует одному элементу массива кватерниона.

Создайте скалярный кватернион с помощью 3х3 матрицы вращения. Задайте, должна ли матрица вращения быть интерпретирована как вращение точки или система координат.

rotationMatrix = [1 0         0; ...
                  0 sqrt(3)/2 0.5; ...
                  0 -0.5      sqrt(3)/2];
quat = quaternion(rotationMatrix,'rotmat','frame')

quat = quaternion
     0.96593 + 0.25882i +       0j +       0k

Можно преобразовать от кватернионов до матриц вращения с помощью rotmat функция. Восстановите rotationMatrix от кватерниона, quat.

rotmat(quat,'frame')

ans = 3×3

    1.0000         0         0
         0    0.8660    0.5000
         0   -0.5000    0.8660

Создайте кватернион путем определения углов Эйлера

Скрипт Open Live Script

Можно создать массив кватерниона N-1 путем определения массива N-3 Углов Эйлера в радианах или степенях.

Углы Эйлера в радианах

Используйте euler синтаксис, чтобы создать скалярный кватернион с помощью 1 3 вектор из Углов Эйлера в радианах. Задайте последовательность вращения Углов Эйлера и представляют ли углы вращение точки или система координат.

E = [pi/2,0,pi/4];
quat = quaternion(E,'euler','ZYX','frame')

quat = quaternion
     0.65328 +  0.2706i +  0.2706j + 0.65328k

Можно преобразовать от кватернионов до Углов Эйлера с помощью euler функция. Восстановите Углы Эйлера, E, от кватерниона, quat.

euler(quat,'ZYX','frame')

ans = 1×3

    1.5708         0    0.7854

Углы Эйлера в градусах

Используйте eulerd синтаксис, чтобы создать скалярный кватернион с помощью 1 3 вектор из Углов Эйлера в градусах. Задайте последовательность вращения Углов Эйлера и представляют ли углы вращение точки или система координат.

E = [90,0,45];
quat = quaternion(E,'eulerd','ZYX','frame')

quat = quaternion
     0.65328 +  0.2706i +  0.2706j + 0.65328k

Можно преобразовать от кватернионов до Углов Эйлера в градусах с помощью eulerd функция. Восстановите Углы Эйлера, E, от кватерниона, quat.

eulerd(quat,'ZYX','frame')

ans = 1×3

   90.0000         0   45.0000

Алгебра кватернионов

Скрипт Open Live Script

Кватернионы формируют некоммутативную ассоциативную алгебру по вещественным числам. Этот пример иллюстрирует правила алгебры кватернионов.

Сложение и вычитание

Сложение кватерниона и вычитание происходят часть частью и являются коммутативными:

Q1 = quaternion(1,2,3,4)

Q1 = quaternion
     1 + 2i + 3j + 4k

Q2 = quaternion(9,8,7,6)

Q2 = quaternion
     9 + 8i + 7j + 6k

Q1plusQ2 = Q1 + Q2

Q1plusQ2 = quaternion
     10 + 10i + 10j + 10k

Q2plusQ1 = Q2 + Q1

Q2plusQ1 = quaternion
     10 + 10i + 10j + 10k

Q1minusQ2 = Q1 - Q2

Q1minusQ2 = quaternion
    -8 - 6i - 4j - 2k

Q2minusQ1 = Q2 - Q1

Q2minusQ1 = quaternion
     8 + 6i + 4j + 2k

Можно также выполнить сложение и вычитание вещественных чисел и кватернионов. Первая часть кватерниона упоминается как действительная часть, в то время как вторые, третьи, и четвертые части упоминаются как вектор. Сложение и вычитание с вещественными числами влияют только на действительную часть кватерниона.

Q1plusRealNumber = Q1 + 5

Q1plusRealNumber = quaternion
     6 + 2i + 3j + 4k

Q1minusRealNumber = Q1 - 5

Q1minusRealNumber = quaternion
    -4 + 2i + 3j + 4k

Умножение

Умножение кватерниона определяется продуктами базисных элементов и дистрибутивного закона. Вспомните, что умножение базисных элементов, i, j, и k, не являюсь коммутативной, и поэтому умножение кватерниона не является коммутативным.

Q1timesQ2 = Q1 * Q2

Q1timesQ2 = quaternion
    -52 + 16i + 54j + 32k

Q2timesQ1 = Q2 * Q1

Q2timesQ1 = quaternion
    -52 + 36i + 14j + 52k

isequal(Q1timesQ2,Q2timesQ1)

ans = logical
   0

Можно также умножить кватернион на вещественное число. Если вы умножаете кватернион на вещественное число, каждая часть кватерниона умножается на вещественное число индивидуально:

Q1times5 = Q1*5

Q1times5 = quaternion
      5 + 10i + 15j + 20k

Умножение кватерниона вещественным числом является коммутативным.

isequal(Q1*5,5*Q1)

ans = logical
   1

Спряжение

Сопряженное комплексное число кватерниона задано таким образом, что каждый элемент векторного фрагмента кватерниона отрицается.

Q1

Q1 = quaternion
     1 + 2i + 3j + 4k

conj(Q1)

ans = quaternion
     1 - 2i - 3j - 4k

Умножение между кватернионом и его сопряженным является коммутативным:

isequal(Q1*conj(Q1),conj(Q1)*Q1)

ans = logical
   1

Манипуляция с массивами кватерниона

Скрипт Open Live Script

Можно организовать кватернионы в векторы, матрицы и многомерные массивы. Функции Built-in MATLAB® были улучшены, чтобы работать с кватернионами.

Конкатенация

Кватернионы обработаны как отдельные объекты во время конкатенации и следуют правилам MATLAB для манипуляции с массивами.

Q1 = quaternion(1,2,3,4);
Q2 = quaternion(9,8,7,6);

qVector = [Q1,Q2]

qVector = 1x2 quaternion array
     1 + 2i + 3j + 4k     9 + 8i + 7j + 6k

Q3 = quaternion(-1,-2,-3,-4);
Q4 = quaternion(-9,-8,-7,-6);

qMatrix = [qVector;Q3,Q4]

qMatrix = 2x2 quaternion array
     1 + 2i + 3j + 4k     9 + 8i + 7j + 6k
    -1 - 2i - 3j - 4k    -9 - 8i - 7j - 6k

qMultiDimensionalArray(:,:,1) = qMatrix;
qMultiDimensionalArray(:,:,2) = qMatrix

qMultiDimensionalArray = 2x2x2 quaternion array
qMultiDimensionalArray(:,:,1) = 

     1 + 2i + 3j + 4k     9 + 8i + 7j + 6k
    -1 - 2i - 3j - 4k    -9 - 8i - 7j - 6k


qMultiDimensionalArray(:,:,2) = 

     1 + 2i + 3j + 4k     9 + 8i + 7j + 6k
    -1 - 2i - 3j - 4k    -9 - 8i - 7j - 6k

Индексация

Чтобы получить доступ или присвоить элементы в массиве кватерниона, используйте индексацию.

qLoc2 = qMultiDimensionalArray(2)

qLoc2 = quaternion
    -1 - 2i - 3j - 4k

Замените кватернион в индексе два с кватернионом один.

qMultiDimensionalArray(2) = ones('quaternion')

qMultiDimensionalArray = 2x2x2 quaternion array
qMultiDimensionalArray(:,:,1) = 

     1 + 2i + 3j + 4k     9 + 8i + 7j + 6k
     1 + 0i + 0j + 0k    -9 - 8i - 7j - 6k


qMultiDimensionalArray(:,:,2) = 

     1 + 2i + 3j + 4k     9 + 8i + 7j + 6k
    -1 - 2i - 3j - 4k    -9 - 8i - 7j - 6k

Изменение

Чтобы изменить размерность массивов кватерниона, используйте reshape функция.

qMatReshaped = reshape(qMatrix,4,1)

qMatReshaped = 4x1 quaternion array
     1 + 2i + 3j + 4k
    -1 - 2i - 3j - 4k
     9 + 8i + 7j + 6k
    -9 - 8i - 7j - 6k

Перемещение

Чтобы транспонировать векторы кватерниона и матрицы, используйте transpose функция.

qMatTransposed = transpose(qMatrix)

qMatTransposed = 2x2 quaternion array
     1 + 2i + 3j + 4k    -1 - 2i - 3j - 4k
     9 + 8i + 7j + 6k    -9 - 8i - 7j - 6k

Перестановка

Чтобы переставить векторы кватерниона, матрицы и многомерные массивы, используют permute функция.

qMultiDimensionalArray

qMultiDimensionalArray = 2x2x2 quaternion array
qMultiDimensionalArray(:,:,1) = 

     1 + 2i + 3j + 4k     9 + 8i + 7j + 6k
     1 + 0i + 0j + 0k    -9 - 8i - 7j - 6k


qMultiDimensionalArray(:,:,2) = 

     1 + 2i + 3j + 4k     9 + 8i + 7j + 6k
    -1 - 2i - 3j - 4k    -9 - 8i - 7j - 6k

qMatPermute = permute(qMultiDimensionalArray,[3,1,2])

qMatPermute = 2x2x2 quaternion array
qMatPermute(:,:,1) = 

     1 + 2i + 3j + 4k     1 + 0i + 0j + 0k
     1 + 2i + 3j + 4k    -1 - 2i - 3j - 4k


qMatPermute(:,:,2) = 

     9 + 8i + 7j + 6k    -9 - 8i - 7j - 6k
     9 + 8i + 7j + 6k    -9 - 8i - 7j - 6k

Документация

quaternion

Описание

Создание

Синтаксис

Описание

Входные параметры

`A,B,C,D` — Части кватерниона
разделенные от запятой массивы, одного размера

`matrix` — Матрица частей кватерниона
N-by-4 матрица

`RV` — Матрица векторов вращения
N-by-3 матрица

`RM` — Матрицы вращения
3х3 матрица | 3 3 N массивом

`PF` — Тип матрицы вращения
`'point'` | `'frame'`

`E` — Матрица Углов Эйлера
N-by-3 матрица

`RS` — Последовательность вращения
вектор символов | скалярная строка

Функции объекта

Примеры

Создайте пустой кватернион

Создайте кватернион путем определения отдельных частей кватерниона

Создайте кватернион путем определения матрицы частей кватерниона

Создайте кватернион путем определения векторов вращения

Создайте кватернион путем определения матриц вращения

Создайте кватернион путем определения углов Эйлера

Алгебра кватернионов

Манипуляция с массивами кватерниона

Расширенные возможности

Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.

Смотрите также

Темы

Документация Sensor Fusion and Tracking Toolbox

Поддержка

Документация

quaternion

Описание

Создание

Синтаксис

Описание

Входные параметры

A,B,C,D — Части кватерниона разделенные от запятой массивы, одного размера

matrix — Матрица частей кватерниона N-by-4 матрица

RV — Матрица векторов вращения N-by-3 матрица

RM — Матрицы вращения 3х3 матрица | 3 3 N массивом

PF — Тип матрицы вращения 'point' | 'frame'

E — Матрица Углов Эйлера N-by-3 матрица

RS — Последовательность вращения вектор символов | скалярная строка

Функции объекта

Примеры

Создайте пустой кватернион

Создайте кватернион путем определения отдельных частей кватерниона

Создайте кватернион путем определения матрицы частей кватерниона

Создайте кватернион путем определения векторов вращения

Создайте кватернион путем определения матриц вращения

Создайте кватернион путем определения углов Эйлера

Алгебра кватернионов

Манипуляция с массивами кватерниона

Расширенные возможности

Генерация кода C/C++ Генерация кода C и C++ с помощью MATLAB® Coder™.

Смотрите также

Темы

Документация Sensor Fusion and Tracking Toolbox

Поддержка

`A,B,C,D` — Части кватерниона
разделенные от запятой массивы, одного размера

`matrix` — Матрица частей кватерниона
N-by-4 матрица

`RV` — Матрица векторов вращения
N-by-3 матрица

`RM` — Матрицы вращения
3х3 матрица | 3 3 N массивом

`PF` — Тип матрицы вращения
`'point'` | `'frame'`

`E` — Матрица Углов Эйлера
N-by-3 матрица

`RS` — Последовательность вращения
вектор символов | скалярная строка

Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.