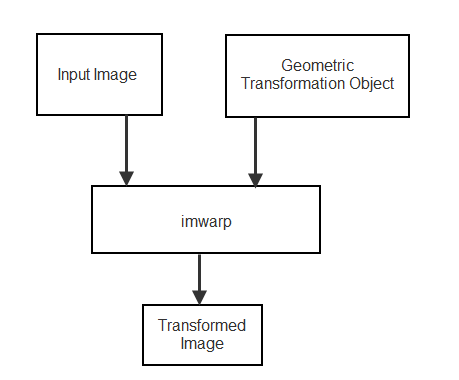
Чтобы выполнить 2D или 3-D геометрическое преобразование, сначала создайте объект геометрического преобразования, который хранит информацию о преобразовании. Затем передайте изображение, которое будет преобразовано и объект геометрического преобразования к imwarp функция. Опционально можно предоставить пространственную информацию о ссылке о входном изображении к imwarp.
Различные типы объектов геометрического преобразования хранят различную информацию о преобразовании.
rigid2d, affine2d, projective2d, rigid3d, и affine3d объекты хранят матрицу преобразования.
geometricTransform2d и geometricTransform3d объекты хранят обратную мудрую точкой функцию отображения, и опционально прямую мудрую точкой функцию отображения.
Другие типы преобразования, включая LocalWeightedMeanTransformation2D, PiecewiseLinearTransformation2D, и PolynomialTransformation2D объекты, сохраните отображение между парами контрольной точки.
Существует несколько способов создать объект геометрического преобразования.
| Приблизьтесь, чтобы создать объект преобразования | affine2d | affine3d |
| projective2d |
| Другие объекты преобразования |
|---|---|---|---|---|---|---|
| Задайте матрицу преобразования | X | X | X | X | ||
| Задайте пользовательскую мудрую точкой функцию отображения | X | |||||
| Оцените преобразование от пар контрольной точки | X | X | X | |||
| Оцените преобразование Используя оптимизацию подобия | X | X | ||||
| Оцените преобразование Используя корреляцию фазы | X |
Если вы знаете матрицу преобразования для геометрического преобразования, вы хотите выполнить, то можно создать rigid2d, affine2d, projective2d, rigid3d, или affine3d геометрическое преобразование возражает непосредственно. Для получения дополнительной информации о создании матрицы преобразования, смотрите Матричное Представление Геометрических преобразований.
Следующий пример задает матрицу преобразования для 2D перевода и создает affine2d объект геометрического преобразования.
xform = [ 1 0 0
0 1 0
40 40 1 ];
tform_translate = affine2d(xform)tform_translate =
affine2d with properties:
T: [3x3 double]
Dimensionality: 2Если у вас есть обратная мудрая точкой функция отображения, то можно задать пользовательское 2D и 3-D геометрическое преобразование с помощью geometricTransform2d и geometricTransform3d объекты соответственно.
Следующий пример задает функцию обратного отображения, которая принимает и возвращает 2D точки в упакованном (x, y) формат. Затем пример создает geometricTransform2d пользовательский объект геометрического преобразования.
inversefn = @(c) [c(:,1)+c(:,2),c(:,1).^2]
inversefn =
function_handle with value:
@(c)[c(:,1)+c(:,2),c(:,1).^2]tform = geometricTransform2d(inversefn)
tform =
geometricTransform2d with properties:
InverseFcn: [function_handle]
ForwardFcn: []
Dimensionality: 2Точно так же следующий пример создает geometricTransform3d пользовательский объект геометрического преобразования использование функции обратного отображения. Пример задает функцию обратного отображения, которая принимает и возвращает 3-D точки в упакованном (x, y, z) формат.
inversefn = @(c)[c(:,1)+c(:,2),c(:,1)-c(:,2),c(:,3).^2]
inversefn =
function_handle with value:
@(c)[c(:,1)+c(:,2),c(:,1)-c(:,2),c(:,3).^2]tform = geometricTransform3d(inversefn)
tform =
geometricTransform3d with properties:
InverseFcn: [function_handle]
ForwardFcn: []
Dimensionality: 3Можно создать объект геометрического преобразования путем передачи двух наборов пар контрольной точки к fitgeotrans функция. fitgeotrans функционируйте автоматически оценивает преобразование от этих точек и возвращает один из объектов геометрического преобразования.
Различные преобразования требуют различного числа точек. Например, аффинные преобразования требуют трех неколлинеарных точек в каждом изображении (треугольник), и проективные преобразования требуют четырех точек (четырехугольник).
Этот пример передает два набора контрольных точек к fitgeotrans, который возвращает affine2d объект геометрического преобразования.
movingPoints = [11 11;21 11; 21 21];
fixedPoints = [51 51;61 51;61 61];
tform_cpp = fitgeotrans(movingPoints,fixedPoints,'affine')
tform_cpp =
affine2d with properties:
T: [3x3 double]
Dimensionality: 2Если у вас есть фиксированное изображение и движущееся изображение, которые немного неправильно выравниваются, то можно использовать imregtform функционируйте, чтобы оценить аффинное геометрическое преобразование, которое выравнивает изображения. imregtform оптимизирует средних квадратичных или Матовые стекла взаимная информационная метрика подобия двух изображений, с помощью регулярного градиентного спуска шага или один плюс один эволюционного оптимизатора. Для получения дополнительной информации смотрите, Создают Оптимизатор и Метрику для Основанной на интенсивности Регистрации Изображений.
Если у вас есть фиксированное изображение и движущееся изображение, которые сильно неправильно выравниваются, то можно использовать imregcorr функционируйте, чтобы оценить аффинное геометрическое преобразование, которое улучшает выравнивание изображения. Можно совершенствовать получившееся преобразование при помощи оптимизации подобия.
После того, как вы задаете преобразование в объекте геометрического преобразования, выполняете преобразование при помощи imwarp функция. При вызывании функции задайте изображение, которое будет преобразовано и объект геометрического преобразования.
imwarp использует геометрическое преобразование, чтобы сопоставить координаты в выходном изображении к соответствующим координатам во входном изображении (обратное отображение). Затем imwarp использует отображение координаты, чтобы интерполировать пиксельные значения во входе, отображают и вычисляют значение выходного пикселя.
imwarp | fitgeotrans | affine2d | affine3d | rigid2d | rigid3d | projective2d | geometricTransform2d | geometricTransform3d