В Формулировке Конструктивных требований как Ограничения H-бесконечности вы описали свои конструктивные требования как ограничение на H ∞ норма передаточной функции с обратной связью H (s).
Следующий шаг должен создать модель Generalized LTI H (s), который включает все фиксированные и настраиваемые элементы системы управления. Модель также включает любые функции взвешивания, которые представляют ваши конструктивные требования. Существует два способа получить эту настраиваемую модель вашей системы управления:
Создать настраиваемую обобщенную линейную модель вашей системы управления с обратной связью в MATLAB®:
Используйте команды такой как tf, zpk, и ss создать числовые линейные модели, которые представляют фиксированные элементы вашей системы управления и любых функций взвешивания, которые представляют ваши конструктивные требования.
Используйте настраиваемые модели (любой Control Design Blocks или Generalized LTI модели), чтобы смоделировать настраиваемые элементы вашей системы управления. Для получения дополнительной информации о настраиваемых моделях, см. Модели с Настраиваемыми Коэффициентами.
Используйте команды соединения моделей такой как series, parallel, и connect создать вашу систему с обратной связью из числовых и настраиваемых моделей.
В этом примере показано, как создать настраиваемую обобщенную линейную модель следующей системы управления для настройки с hinfstruct.
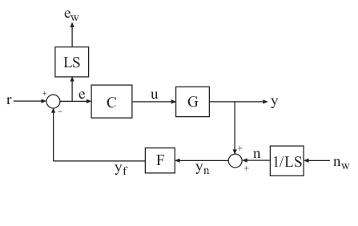
Эта блок-схема представляет блок главного диска (HDA) в жестком диске. Архитектура включает объект G в обратной связи с ПИ-контроллером C и фильтр lowpass, F = a/(s+a). Настраиваемые параметры являются усилениями PI C и параметр фильтра a.
Блок-схема также включает функции взвешивания LS и 1/LS, которые описывают формирующие цикл требования. Позволенный T (s) обозначают передаточную функцию с обратной связью от входных параметров (r, nw) к выходным параметрам (y, ew). Затем H ∞ ограничение:
приблизительно осуществляет целевую форму ответа разомкнутого контура LS. В данном примере целевая форма цикла
Это значение LS соответствует следующей форме ответа разомкнутого контура.
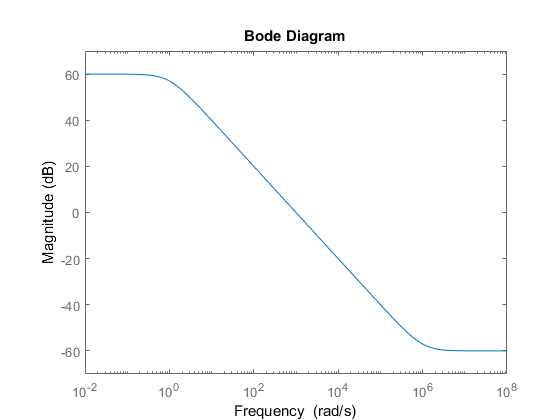
Настроить систему управления HDA с hinfstruct, создайте настраиваемую модель системы с обратной связью T (s), включая функции взвешивания, можно следующим образом.
Загрузите объект G из сохраненного файла.
load hinfstruct_demo G
G 9-й порядок пространство состояний SISO (ss) модель.
Создайте настраиваемую модель ПИ-контроллера.
Можно использовать предопределенный Блок Системы управления tunablePID представлять настраиваемый ПИ-контроллер.
C = tunablePID('C','pi');
Создайте настраиваемую модель фильтра lowpass.
Поскольку нет никакого предопределенного Блока Системы управления для фильтра F = a/(s+a)Использование realp представлять настраиваемый параметр фильтра a. Затем создайте настраиваемое genss модель, представляющая фильтр.
a = realp('a',1);
F = tf(a,[1 a]);Укажите, что целевой цикл формирует LC.
wc = 1000;
s = tf('s');
LS = (1+0.001*s/wc)/(0.001+s/wc);Пометьте вводы и выводы всех компонентов системы управления.
Маркировка I/Os позволяет вам соединять элементы, чтобы создать систему с обратной связью T (s).
Wn = 1/LS; Wn.InputName = 'nw'; Wn.OutputName = 'n'; We = LS; We.InputName = 'e'; We.OutputName = 'ew'; C.InputName = 'e'; C.OutputName = 'u'; F.InputName = 'yn'; F.OutputName = 'yf';
Задайте соединения подведения итогов в терминах меток ввода-вывода других компонентов системы управления.
Sum1 = sumblk('e = r - yf'); Sum2 = sumblk('yn = y + n');
Использование connect объединить все элементы в полную модель системы с обратной связью T (s).
T0 = connect(G,Wn,We,C,F,Sum1,Sum2,{'r','nw'},{'y','ew'});T0 isa genss объект, который является моделью Generalized LTI, представляющей систему управления с обратной связью функциями взвешивания. Blocks свойство T0 содержит настраиваемые блоки C и a.
T0.Blocks
ans = struct with fields:
C: [1x1 tunablePID]
a: [1x1 realp]
Для получения дополнительной информации об обобщенных моделях систем управления, которые включают и числовые и настраиваемые компоненты, см. Модели с Настраиваемыми Коэффициентами.
Можно теперь использовать hinfstruct настроить параметры этой системы управления. Смотрите Мелодию Параметры Контроллера.
В этом примере, модели T0 системы управления модель непрерывного времени (T0.Ts = 0). Можно также использовать hinfstruct с моделью дискретного времени, при условии, что вы задаете определенный шаг расчета (T0.Ts ≠ –1).
Если у вас есть модель Simulink вашей системы управления и программное обеспечение Simulink Control Design, использовать slTuner (Simulink Control Design), чтобы создать интерфейс к модели Simulink вашей системы управления. Когда вы создаете интерфейс, вы задаете который блоки настроить вашу модель. slTuner интерфейс позволяет вам извлекать модель с обратной связью для настройки с hinfstruct. (Основанная на Simulink функциональность не доступна в MATLAB Online™.)
В этом примере показано, как создать настраиваемую обобщенную линейную модель системы управления в модели Simulink rct_diskdrive.
Создать обобщенную линейную модель этой системы управления (включая формирующие цикл функции взвешивания):
Откройте модель.
open('rct_diskdrive');

Создайте slTuner взаимодействуйте через интерфейс к модели. Интерфейс позволяет вам задавать настраиваемые блоки, и извлечение линеаризовало разомкнутый контур и ответы с обратной связью. (Для получения дополнительной информации об интерфейсе, смотрите slTuner (Simulink Control Design) страница с описанием.)
ST0 = slTuner('rct_diskdrive',{'C','F'});
Эта команда задает тот C и F настраиваемые блоки в модели. slTuner интерфейс автоматически параметризует эти блоки. Параметризация по умолчанию блока F передаточной функции передаточная функция двумя свободными параметрами. Поскольку F фильтр lowpass, необходимо ограничить его коэффициенты. Для этого задайте пользовательскую параметризацию F.
a = realp('a',1); % filter coefficient setBlockParam(ST0,'F',tf(a,[1 a]));
Извлеките настраиваемую модель передаточной функции с обратной связью, которую вы хотите настроить.
T0 = getIOTransfer(ST0,{'r','n'},{'y','e'});
Эта команда возвращает a genss модель линеаризовавшей передаточной функции с обратной связью из ссылки и шума вводит r,n к измерению и ошибке выходные параметры y,e. Вывод ошибок необходим для формирующей цикл функции взвешивания.
Задайте формирующие цикл функции взвешивания и добавьте их к T0.
wc = 1000;
s = tf('s');
LS = (1+0.001*s/wc)/(0.001+s/wc);
T0 = blkdiag(1,LS) * T0 * blkdiag(1,1/LS);
Обобщенная линейная модель T0 настраиваемая модель передаточной функции с обратной связью T (s), обсужденный в Примере: Моделирование Системы управления С Настраиваемым ПИ-контроллером и Настраиваемым Фильтром. T (s) является взвешенной моделью с обратной связью системы управления rct_diskdrive. Настройка T0 осуществлять H ∞ ограничение
приблизительно осуществляет целевую форму цикла LS.
Можно теперь использовать hinfstruct настроить параметры этой системы управления. Смотрите Мелодию Параметры Контроллера.