Частотно-модулированный косинус
Сгенерируйте щебет с линейным мгновенным отклонением частоты. Щебет производится на уровне 1 кГц в течение 2 секунд. Мгновенная частота 0 в t = 0 и пересекает 250 Гц в t = 1 секунда.
t = 0:1/1e3:2; y = chirp(t,0,1,250);
Вычислите и постройте спектрограмму щебета. Разделите сигнал на сегменты, таким образом, что разрешение времени составляет 0,1 секунды. Задайте 99% перекрытия между смежными сегментами и спектральной утечкой 0,85.
pspectrum(y,1e3,'spectrogram','TimeResolution',0.1, ... 'OverlapPercent',99,'Leakage',0.85)

Сгенерируйте щебет с квадратичным мгновенным отклонением частоты. Щебет производится на уровне 1 кГц в течение 2 секунд. Мгновенная частота составляет 100 Гц в t = 0 и пересекает 200 Гц в t = 1 секунда.
t = 0:1/1e3:2;
y = chirp(t,100,1,200,'quadratic');Вычислите и постройте спектрограмму щебета. Разделите сигнал на сегменты, таким образом, что разрешение времени составляет 0,1 секунды. Задайте 99% перекрытия между смежными сегментами и спектральной утечкой 0,85.
pspectrum(y,1e3,'spectrogram','TimeResolution',0.1, ... 'OverlapPercent',99,'Leakage',0.85)

Сгенерируйте выпуклый квадратичный щебет, произведенный на уровне 1 кГц в течение 2 секунд. Мгновенная частота составляет 400 Гц в t = 0 и пересекает 300 Гц в t = 1 секунда.
t = 0:1/1e3:2; fo = 400; f1 = 300; y = chirp(t,fo,1,f1,'quadratic',[],'convex');
Вычислите и постройте спектрограмму щебета. Разделите сигнал на сегменты, таким образом, что разрешение времени составляет 0,1 секунды. Задайте 99% перекрытия между смежными сегментами и спектральной утечкой 0,85.
pspectrum(y,1e3,'spectrogram','TimeResolution',0.1, ... 'OverlapPercent',99,'Leakage',0.85)

Сгенерируйте вогнутый квадратичный щебет, произведенный на уровне 1 кГц в течение 4 секунд. Задайте временной вектор так, чтобы мгновенная частота была симметрична о средней точке интервала выборки с минимальной частотой 100 Гц и максимальной частотой 500 Гц.
t = -2:1/1e3:2; fo = 100; f1 = 200; y = chirp(t,fo,1,f1,'quadratic',[],'concave');
Вычислите и постройте спектрограмму щебета. Разделите сигнал на сегменты, таким образом, что разрешение времени составляет 0,1 секунды. Задайте 99% перекрытия между смежными сегментами и спектральной утечкой 0,85.
pspectrum(y,t,'spectrogram','TimeResolution',0.1, ... 'OverlapPercent',99,'Leakage',0.85)

Сгенерируйте логарифмический щебет, произведенный на уровне 1 кГц в течение 10 секунд. Мгновенная частота составляет 10 Гц первоначально и 400 Гц в конце.
t = 0:1/1e3:10;
fo = 10;
f1 = 400;
y = chirp(t,fo,10,f1,'logarithmic');Вычислите и постройте спектрограмму щебета. Разделите сигнал на сегменты, таким образом, что разрешение времени составляет 0,2 секунды. Задайте 99% перекрытия между смежными сегментами и спектральной утечкой 0,85.
pspectrum(y,t,'spectrogram','TimeResolution',0.2, ... 'OverlapPercent',99,'Leakage',0.85)

Используйте логарифмический масштаб для оси частоты. Спектрограмма становится линией с высокой неопределенностью в низких частотах.
ax = gca;
ax.YScale = 'log';
Сгенерируйте комплексный линейный щебет, произведенный на уровне 1 кГц в течение 10 секунд. Мгновенная частота составляет-200 Гц первоначально и 300 Гц в конце. Начальная фаза является нулем.
t = 0:1/1e3:10; fo = -200; f1 = 300; y = chirp(t,fo,t(end),f1,'linear',0,'complex');
Вычислите и постройте спектрограмму щебета. Разделите сигнал на сегменты, таким образом, что разрешение времени составляет 0,2 секунды. Задайте 99% перекрытия между смежными сегментами и спектральной утечкой 0,85.
pspectrum(y,t,'spectrogram','TimeResolution',0.2, ... 'OverlapPercent',99,'Leakage',0.85)

Проверьте, что комплексный чирплет имеет действительные и мнимые части, которые равны, но с разность фаз.
x = chirp(t,fo,t(end),f1,'linear',0) + 1j*chirp(t,fo,t(end),f1,'linear',-90); pspectrum(x,t,'spectrogram','TimeResolution',0.2, ... 'OverlapPercent',99,'Leakage',0.85)

t — Массив времениМассив времени в виде вектора.
Типы данных: single | double
f0 — Мгновенная частота во время 0Начальная мгновенная частота во время 0 в виде действительного скаляра описывается в Гц.
Типы данных: single | double
t1 — Ссылочное времяСсылочное время в виде положительной скалярной величины описывается в секундах.
Типы данных: single | double
f1 — Мгновенная частота во время t1Мгновенная частота во время t1В виде действительного скаляра, описанного в Гц.
Типы данных: single | double
method — Разверните метод'linear' (значение по умолчанию) | 'quadratic' | 'logarithmic'Разверните метод в виде 'linear', 'quadratic', или 'logarithmic'.
'linear' — Указывает, что мгновенная частота развертывает fi (t), данный
где
и значение по умолчанию для f 0 0. Коэффициент β гарантирует, что желаемая частота устанавливает точки останова f 1 во время t 1, обеспечен.
'quadratic' — Указывает, что мгновенная частота развертывает fi (t), данный
где
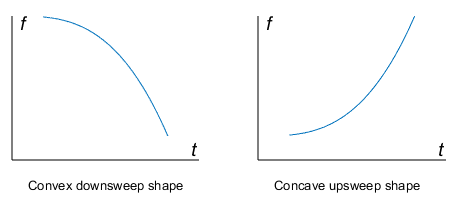
и значение по умолчанию для f 0 0. Если f 0> f 1 (downsweep), форма по умолчанию выпукла. Если f 0 < f 1 (upsweep), форма по умолчанию является вогнутой.
'logarithmic' — Указывает, что мгновенная частота развертывает fi (t), данный
где
и значение по умолчанию для f 0 равняется 10–6.
phi — Начальная фазаНачальная фаза в виде положительной скалярной величины, описанной в градусах.
Типы данных: single | double
shape — Форма спектрограммы квадратичного щебета'convex' | 'concave'Форма спектрограммы квадратичного щебета в виде 'convex' или 'concave'. shape описывает форму параболы относительно положительной оси частоты. Если не заданный, shape 'convex' для downsweep случая с f 0> f 1, и 'concave' для upsweep случая с f 0 <f 1.
cplx — Выведите сложность'real' (значение по умолчанию) | 'complex'Выведите сложность в виде 'real' или 'complex'.
y — Сигнал частотно-модулированного косинусаСигнал частотно-модулированного косинуса, возвращенный как вектор.
backgroundPool или ускорьте код с Parallel Computing Toolbox™ ThreadPool.Эта функция полностью поддерживает основанные на потоке среды. Для получения дополнительной информации смотрите функции MATLAB Запуска в Основанной на потоке Среде.
cos | diric | gauspuls | pulstran | rectpuls | sawtooth | sin | sinc | square | tripuls
У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.