Адаптивное управление моделью

Адаптивное управление моделью - ссылкой

Адаптивное управление моделью - ссылкой (MRAC) является основанным на модели, алгоритмом адаптивного управления в реальном времени, который вычисляет действия управления, чтобы заставить неопределенную управляемую систему отследить поведение данной ссылочной модели объекта управления. Используя Simulink^® Программное обеспечение Control Design™, можно реализовать MRAC использование блока Model Reference Adaptive Control.

Следующий рисунок показывает структуру контроллера MRAC.

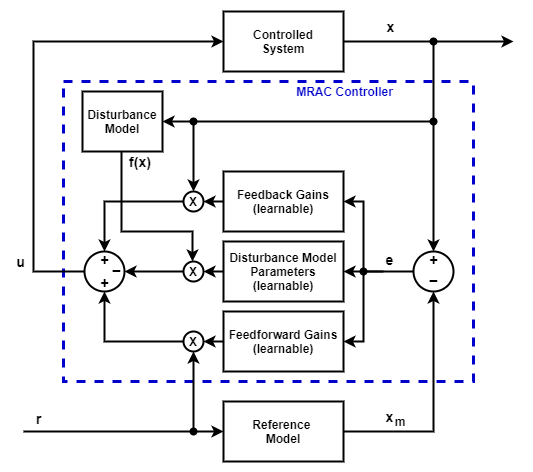
MRAC controller that finds the error between the reference model and plant states and computes control actions using learnable gains and disturbance model.

Цель контроллера состоит в том, чтобы сделать состояния (x) управляемой системной дорожки состояния (_xm) образца модели для данного опорного сигнала (r). Для получения дополнительной информации об управляемой системе и образцах модели, смотрите Номинал и Образцы модели. Диспетчер MRAC использует следующий процесс, чтобы сгенерировать управляющий сигнал.

Вычислите ошибку e между состояниями управляемой системы и состояниями образца модели.
Вычислите функции ϕ(x) для внутренней модели системных воздействий и неопределенности.
Обновите параметры веса возмущения на основе ошибки e.
Обновите значения обратной связи и усилений прямого распространения на основе ошибки e. Можно принять решение сделать, чтобы контроллер адаптировал усиления прямого распространения, усиления обратной связи или обоих.
Примените обновленные коэффициенты усиления и параметры к опорному сигналу, состояниям объекта и функциям возмущения.
Вычислите действие управления u. Для получения дополнительной информации смотрите Структуру управления.

Номинал и образцы модели

Управляемая система, которая обычно показывает неопределенность моделирования и внешние возмущения, имеет следующее номинальное уравнение состояния. Эта модель представляет номинальное поведение, которое вы ожидаете от объекта.

$\dot{x} (t) = A x (t) + B (u (t) + f (x))$

Здесь:

x (t) является состоянием системы, которой вы хотите управлять.
u (t) является входом управления.
A является постоянной матрицей Грина.
B является постоянным управлением эффективная матрица.
f (x) является совпадающей неопределенностью в системе.

Ссылочная модель объекта управления является идеальной системой, которая характеризует желаемое поведение, которого вы хотите достигнуть на практике.

${\dot{x}}_{m} (t) = A_{m} x_{m} (t) + B_{m} r (t)$

Здесь:

r (t) является сигналом внешней ссылки
_xm (t) является состоянием ссылочной модели объекта управления. Поскольку r (t) известен, можно симулировать образец модели, чтобы получить _xm (t).
_Am является матрицей постоянного состояния. Для устойчивого образца модели _Am должен быть матрицей Гурвица, для которой каждое собственное значение должно иметь строго отрицательную действительную часть.
_Bm является управлением эффективная матрица.

Структура управления

MRAC вычисляет вход u управления (t) с помощью следующей структуры управления.

$\begin{array}{l} u (t) = k_{x} x (t) + k_{r} r (t) - u_{a d} \\ u_{a d} = w^{T} ϕ (x) \end{array}$

Здесь:

_kx является матрицей усиления обратной связи.
_kr является матрицей усиления прямого распространения.
_uad является компонентом адаптивного управления, выведенным из возмущения.
ϕ (x) содержит особенности модели воздействия и неопределенности. Для получения дополнительной информации об особенностях модели смотрите Особенности модели Воздействия и Неопределенности.
w является вектором веса адаптивного управления.

Диспетчер MRAC может изучить значения _kx, _kr и w в режиме реального времени.

Когда вы заменяете структурой управления в номинальную модель и упрощаете результат, вы получаете следующее уравнение состояния.

$\dot{x} (t) = (A + B k_{x}) x (t) + B k_{r} r (t) + B (f (x) - w^{T} ϕ (x))$

Неопределенность и ошибочная динамика

Используя универсальное свойство приближения нейронных сетей, можно принять, что идеальная нейронная сеть с неизвестными идеальными весами может параметрировать истинную неопределенность.

$f (x) = w^{* T} ϕ (x) + ε$

Здесь, w^* содержит неизвестные идеальные веса, и ε является ошибкой приближения.

Далее, если вы задаете ошибку вектора веса как $\tilde{w} = w^{*} - w$ и замените им в структуру управления, вы получаете следующее уравнение состояния.

$\dot{x} (t) = (A + B k_{x}) x (t) + B k_{r} r (t) + B ({\tilde{w}}^{T} ϕ (x) + ε)$

Целью контроллера MRAC является асимптотическая сходимость состояния, отслеживающего ошибку e (t), чтобы обнулить.

$\begin{array}{l} e (t) = x (t) - x_{m} (t) \\ \dot{e} (t) = \dot{x} (t) - {\dot{x}}_{m} (t) \end{array}$

Замените структурой управления и уравнениями образца модели, чтобы получить следующее уравнение для ошибочной динамики.

$\dot{e} (t) = (A + B k_{x}) x (t) + B k_{r} r (t) + B ({\tilde{w}}^{T} ϕ (x) + ε) - A_{m} x_{m} (t) - B_{m} r (t)$

Можно переписать это уравнение можно следующим образом.

$\begin{array}{l} \dot{e} (t) = A_{m} e (t) + B {\tilde{k}}_{x} x (t) + B {\tilde{k}}_{r} r (t) + B ({\tilde{w}}^{T} ϕ (x) + ε) \\ {\tilde{k}}_{x} = k_{x}^{*} - k_{x} \\ {\tilde{k}}_{r} = k_{r}^{*} - k_{r} \end{array}$

Здесь, ${\tilde{k}}_{x}$ и ${\tilde{k}}_{r}$ обратная связь и ошибки усиления прямого распространения, соответственно. $k_{x}^{*}$ и $k_{r}^{*}$ неизвестная идеальная обратная связь и усиления прямого распространения.

Обновления параметра

Чтобы вывести уравнения обновления параметра MRAC, сначала задайте следующую функцию Ляпунова на основе ошибочной динамики.

$V (e, {\tilde{k}}_{x}, {\tilde{k}}_{r}, \tilde{w}) = e^{T} Q e + \frac{Γ_{x} {\tilde{k}}_{x}^{2}}{2} + \frac{Γ_{r} {\tilde{k}}_{r}^{2}}{2} + \frac{{\tilde{w}}^{T} Γ_{w} \tilde{w}}{2}$

Здесь, _Γx, _Γr и _Γw являются скоростями обучения для обновлений параметра. Q является матрицей взвешивания для ошибок отслеживания состояния.

Чтобы получить следующие уравнения обновления параметра, возьмите производную Ли предыдущей функции Ляпунова вдоль ошибочной динамики и приравняйте его, чтобы обнулить.

$\begin{array}{l} {\dot{k}}_{x} = Γ_{x} x (t) e^{T} (t) P B \\ {\dot{k}}_{r} = Γ_{r} x (t) e^{T} (t) P B \\ {\dot{w}}_{x} = Γ_{w} ϕ (t) e^{T} (t) P B \end{array}$

Здесь, P является решением следующей функции Ляпунова на основе матрицы состояния образца модели.

$A_{m}^{T} P + P A_{m} + Q = 0$

Изучение модификации

Чтобы добавить робастность на уровнях высшего образования, можно изменить обновления параметра, чтобы включать дополнительный термин импульса. Можно выбрать один из двух возможных методов модификации изучения: модификация сигмы и электронная модификация.

Для модификации сигмы термин импульса для каждого обновления параметра является продуктом параметра веса импульса σ и текущее значение параметров.

$\begin{array}{l} {\dot{k}}_{x} = Γ_{x} x (t) e^{T} (t) P B + σ k_{x} \\ {\dot{k}}_{r} = Γ_{r} x (t) e^{T} (t) P B + σ k_{x} \\ {\dot{w}}_{x} = Γ_{w} ϕ (t) e^{T} (t) P B + σ w \end{array}$

Для электронной модификации контроллер масштабирует термин импульса модификации сигмы нормой вектора ошибок.

$\begin{array}{l} {\dot{k}}_{x} = Γ_{x} x (t) e^{T} (t) P B + σ | e (t) | k_{x} \\ {\dot{k}}_{r} = Γ_{r} x (t) e^{T} (t) P B + σ | e (t) | k_{x} \\ {\dot{w}}_{x} = Γ_{w} ϕ (t) e^{T} (t) P B + σ | e (t) | w \end{array}$

Чтобы настроить объем модификации изучения для любого метода, измените значение параметра веса импульса σ.

Воздействие и особенности модели неопределенности

Блок Model Reference Adaptive Control обеспечивает внутреннюю модель _uad воздействия и неопределенности модели в управляемой системе.

$u_{a d} = w^{T} ϕ (x)$

Здесь, ϕ (x) является вектором из особенностей модели. w является вектором веса адаптивного управления, который контроллер обновляет в режиме реального времени.

Чтобы задать ϕ (x), можно использовать одно из следующих определений функции.

Вектор состояния управляемого объекта — Этот подход может под - представлять неопределенность и выполнять плохо. Используйте эту опцию, когда воздействие и неопределенность модели будут линейны. Используя вектор состояния может также быть полезная начальная точка, когда вы не знаете сложности воздействия и неопределенности модели.
Гауссовы радиальные основные функции — Использование эта опция, когда воздействие и неопределенность модели нелинейны и структура возмущения, неизвестно.
Внешний источник, предоставленный блоку контроллера — Использование эта опция, чтобы задать ваш собственный характеристический вектор. Можно использовать эту опцию, когда вы знаете структуру модели воздействия и неопределенности. Например, можно использовать пользовательский характеристический вектор, чтобы идентифицировать определенные неизвестные параметры объекта.

Документация