Dynamic Steering

Динамическое регулирование для Акермана, реечного механизма и параллельных рулевых механизмов

Библиотека:
Vehicle Dynamics Blockset / регулирование

Описание

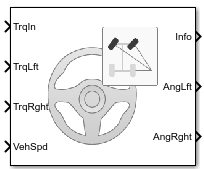
Блок Dynamic Steering реализует динамическое регулирование, чтобы вычислить углы колеса для Акермана, реечного механизма и параллельных рулевых механизмов. Блок использует входной крутящий момент руля, правильный крутящий момент колеса и оставленный крутящий момент колеса, чтобы вычислить углы колеса. Блок использует систему координат транспортного средства.

Если вы выбираете Power assist, можно указать, что крутящий момент помогает интерполяционной таблице, которая является функцией скорости транспортного средства и входного крутящего момента руля. Блок использует входной крутящий момент руля, и крутящий момент помогают вычислять держащуюся динамику.

Чтобы задать держащийся тип, используйте параметр Type.

Установка	Блокируйте реализацию
`Ackerman`	Идеал Акерман, держащийся. Углы колеса имеют общий центр круга превращения.
`Rack and pinion`	Идеальное регулирование реечного механизма. Механизмы преобразуют держащееся вращение в линейное движение.
`Parallel`	Параллельное регулирование. Углы колеса равны.

Чтобы задать тип данных для рулевого механизма, используйте параметр Parametrized by.

Установка	Блокируйте реализацию
`Constant`	Рулевой механизм использует постоянные данные о параметре.
`Lookup table`	Рулевой механизм реализует таблицы для данных о параметре.

Используйте параметр Location, чтобы задать переднее или заднее регулирование.

Установка	Реализация
Front	Переднее регулирование
Rear	Заднее регулирование

Установка

Реализация

Front

Переднее регулирование

Figure of front steering turning right

Rear

Заднее регулирование

Figure of rear steering turning right

Динамика

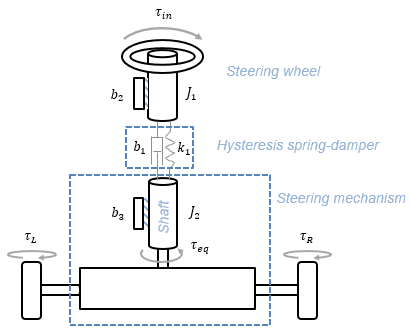
Чтобы вычислить держащуюся динамику, блок Dynamic Steering моделирует руль, вал, рулевой механизм, гистерезис, и, опционально, степень помогают.

Figure of steering wheel, spring damper, and steering mechanism

Вычисление	Уравнения
Рулевая колонка и держащаяся динамика вала	$J_{1} {\ddot{θ}}_{1} = τ_{i n} - b_{2} {\dot{θ}}_{1} - τ_{h y s}$ $J_{2} {\ddot{θ}}_{2} = τ_{e q} - b_{3} {\dot{θ}}_{2} + τ_{h y s} - τ_{f r i c}$
Гистерезисный пружинный демпфер	$\begin{array}{l} δ = θ_{1} - θ_{2} \\ Δ δ = δ_{c u r r e n t} - δ_{p r e v i o u s} \\ τ_{h y s} = (b_{1} \dot{δ} - k_{1} δ) (1 + \exp (- \frac{\| Δ δ \|}{β})) \\ β = {\begin{matrix} β_{u} когда δ > 0 \\ β_{l} когда δ \leq 0 \end{matrix} \end{array}$
Дополнительная степень помогает	$\begin{array}{l} τ_{a s t} = f_{t r q} (v, τ_{i n}) \\ J_{1} {\ddot{θ}}_{1} = τ_{i n} + τ_{a s t} - b_{2} {\dot{θ}}_{1} - τ_{h y s} \\ J_{2} {\ddot{θ}}_{2} = τ_{e q} + τ_{a s t} - b_{3} {\dot{θ}}_{2} + τ_{h y s} - τ_{f r i c} \end{array}$

Вычисление

Уравнения

Рулевая колонка и держащаяся динамика вала

$J_{1} {\ddot{θ}}_{1} = τ_{i n} - b_{2} {\dot{θ}}_{1} - τ_{h y s}$

$J_{2} {\ddot{θ}}_{2} = τ_{e q} - b_{3} {\dot{θ}}_{2} + τ_{h y s} - τ_{f r i c}$

Гистерезисный пружинный демпфер

$\begin{array}{l} δ = θ_{1} - θ_{2} \\ Δ δ = δ_{c u r r e n t} - δ_{p r e v i o u s} \\ τ_{h y s} = (b_{1} \dot{δ} - k_{1} δ) (1 + \exp (- \frac{| Δ δ |}{β})) \\ β = {\begin{matrix} β_{u} когда δ > 0 \\ β_{l} когда δ \leq 0 \end{matrix} \end{array}$

Дополнительная степень помогает

$\begin{array}{l} τ_{a s t} = f_{t r q} (v, τ_{i n}) \\ J_{1} {\ddot{θ}}_{1} = τ_{i n} + τ_{a s t} - b_{2} {\dot{θ}}_{1} - τ_{h y s} \\ J_{2} {\ddot{θ}}_{2} = τ_{e q} + τ_{a s t} - b_{3} {\dot{θ}}_{2} + τ_{h y s} - τ_{f r i c} \end{array}$

Рисунок и уравнения используют эти переменные.

_J1	Инерция руля
_J2	Инерция рулевого механизма
$θ_{1}, {\dot{θ}}_{1}, {\ddot{θ}}_{1}$	Угол руля, скорость вращения и угловое ускорение, соответственно
$θ_{2}, {\dot{θ}}_{2}, {\ddot{θ}}_{2}$	Угол вала, скорость вращения и угловое ускорение, соответственно
_b1, _k1	Гистерезисные пружинные и вязкие коэффициенты демпфирования, соответственно
_b2	Руль вязкий коэффициент демпфирования
_b3	Коэффициент демпфирования рулевого механизма
_τhys	Гистерезисный крутящий момент затухания пружины
_τfric	Момент трения рулевого механизма
_τeq	Колесо эквивалентный крутящий момент
_τast	Крутящий момент помогает
_βu , _βl	Верхние и более низкие гистерезисные модификаторы, соответственно
v	Скорость транспортного средства
_ƒtrq	Крутящий момент помогает интерполяционной таблице

Регулирование типов

Акерман

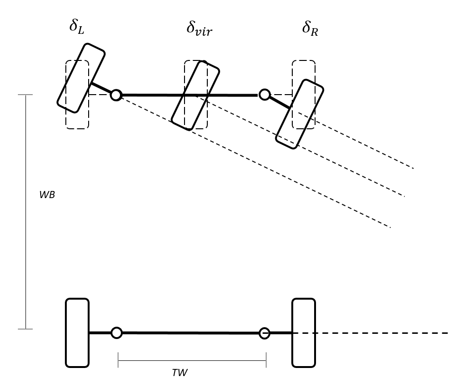
Для идеала Акерман, держащийся, углы колеса имеют общий круг превращения.

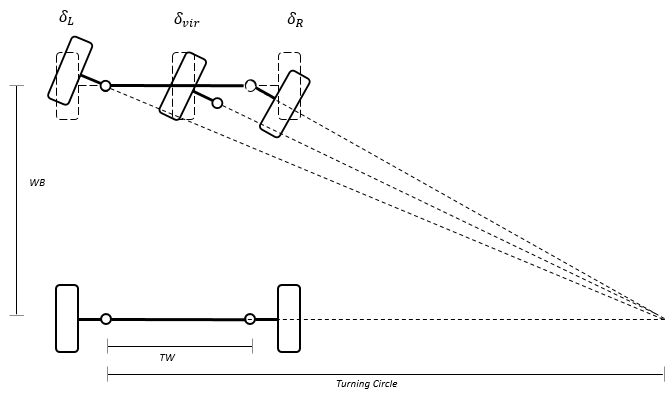
Figure of Ackerman steering turning right around turning circle

Чтобы вычислить держащиеся углы, блок использует эти уравнения.

$\begin{array}{l} \cot (δ_{L}) - \cot (δ_{R}) = \frac{T W}{W B} \\ δ_{v i r} = \frac{δ_{i n}}{γ} \\ δ_{L} = \tan^{- 1} (\frac{W B \tan (δ_{v i r})}{W B - 0.5 T W \tan (δ_{v i r})}) \\ δ_{R} = \tan^{- 1} (\frac{W B \tan (δ_{v i r})}{W B + 0.5 T W \tan (δ_{v i r})}) \end{array}$

Рисунок и уравнения используют эти переменные.

_δin	Регулирование угла
_δL	Оставленный угол колеса
_δR	Правильный угол колеса
_δvir	Виртуальный угол колеса
TW	Ширина дорожки
WB	Основа колеса
γ	Регулирование отношения

Реечный механизм

Для идеального регулирования реечного механизма механизмы преобразуют держащееся вращение в линейное движение.

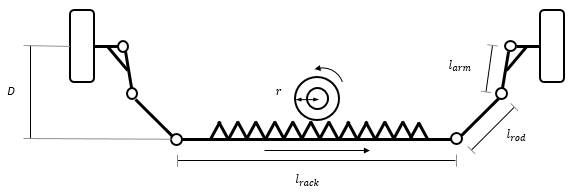
Figure of rack, rod, and arm in rack and pinion steering mechanism

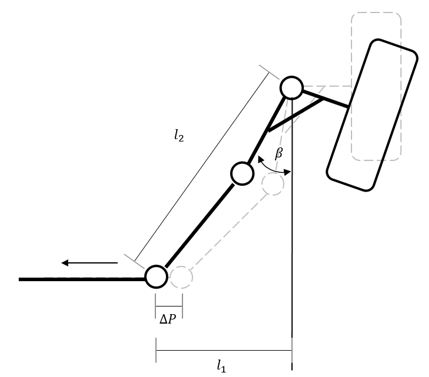
Figure of rod in rack and pinion steering mechanism

Чтобы вычислить держащиеся углы, блок использует эти уравнения.

$\begin{array}{l} l_{1} = \frac{T W - l_{r a c k}}{2} - Δ P \\ l_{2}^{2} = l_{1}^{2} + D^{2} \\ Δ P = r δ_{i n} \\ β = \frac{π}{2} - \tan^{- 1} [\frac{D}{l_{1}}] - \cos^{- 1} [\frac{l_{a r m}^{2} + l_{2}^{2} - l_{r o d}^{2}}{2 l_{a r m} l_{2}}] \end{array}$

Рисунок и уравнения используют эти переменные.

_δin	Угол руля
_δL	Оставленный угол колеса
_δR	Правильный угол колеса
TW	Ширина дорожки
r	Свяжите радиус
ΔP	Линейное изменение в положении стойки
D	Расстояние между передней осью и стойкой
_lrack	Установите случающуюся длину в стойку
_larm	Регулирование длины руки
_lrod	Свяжите длину стержня

Параллель

Для параллельного регулирования углы колеса равны.

Figure parallel steering where wheel angles are equal

Чтобы вычислить держащиеся углы, блок использует это уравнение.

$δ_{R} = δ_{L} = \frac{δ_{i n}}{γ}$

Рисунок и уравнения используют эти переменные.

_δin	Угол руля
_δL	Оставленный угол колеса
_δR	Правильный угол колеса
γ	Регулирование отношения

Порты

Входной параметр

развернуть все

`TrqIn` — Крутящий момент
`scalar`

Крутящий момент, _τin, в N · m.

`TrqLft` — Оставленный крутящий момент колеса
`scalar`

Оставленный крутящий момент колеса, _τL, в N · m.

`TrqRght` — Правильный крутящий момент колеса
`scalar`

Правильный крутящий момент колеса, _τR, в N · m.

`VehSpd` — Скорость транспортного средства
`scalar`

Скорость транспортного средства, v, в m/s.

Зависимости

Создать VehSpd, выберите Power assist.

Вывод

развернуть все

`Info` — Сигнал шины
шина

Сигнал шины содержит эти вычисления блока.

Сигнал	Описание	Модуль
`StrgWhlAng`	Угол руля	рад
`StrgWhlSpd`	Скорость вращения руля	рад/с
`ShftAng`	Угол вала	рад
`ShftSpd`	Угловая скорость вала	рад/с
`AngLft`	Оставленный угол колеса	рад
`SpdLft`	Оставленная скорость вращения колеса	рад/с
`AngRght`	Правильный угол колеса	рад
`SpdRght`	Правильная скорость вращения колеса	рад/с
`TrqAst`	Крутящий момент помогает	N·
`PwrAst`	Степень помогает	W
`PwrLoss`	Потери мощности	W
`InstStrgRatio`	Мгновенное руководящее отношение	N/A

`AngLft` — Оставленный угол колеса
`scalar`

Оставленный угол колеса, _δL, в рад.

`AngRght` — Правильный угол колеса
`scalar`

Правильный угол колеса, _δR, в рад.

Параметры

развернуть все

`Type` — Выберите держащийся тип
`Rack and pinion` (значение по умолчанию) | `Ackerman` | `Parallel`

Чтобы задать держащийся тип, используйте параметр Type.

Установка	Блокируйте реализацию
`Ackerman`	Идеал Акерман, держащийся. Углы колеса имеют общий центр круга превращения.
`Rack and pinion`	Идеальное регулирование реечного механизма. Механизмы преобразуют держащееся вращение в линейное движение.
`Parallel`	Параллельное регулирование. Углы колеса равны.

Зависимости

Эта таблица суммирует Type и зависимости от параметра Parametrized by.

Ввод	Параметрированный	Создает параметры
`Ackerman`	`Constant`	Track width, TrckWdth Wheel base, WhlBase Steering range, StrgRng Steering ratio, StrgRatio
`Ackerman`	`Lookup table`	Track width, TrckWdth Wheel base, WhlBase Steering range, StrgRng Steering angle breakpoints, StrgAngBpts Steering ratio table, StrgRatioTbl
`Rack and pinion`	`Constant`	Track width, TrckWdth Steering range, StrgRng Steering arm length, StrgArmLngth Rack casing length, RckCsLngth Tie rod length, TieRodLngth Distance between front axis and rack, D Pinion radius, PnnRadius
`Rack and pinion`	`Lookup table`	Track width, TrckWdth Steering range, StrgRng Steering angle breakpoints, StrgAngBpts Steering arm length, StrgArmLngth Rack casing length, RckCsLngth Tie rod length, TieRodLngth Distance between front axis and rack, D Pinion radius, PnnRadiusTbl
`Parallel`	`Constant`	Steering range, StrgRng Steering ratio, StrgRatio
`Parallel`	`Lookup table`	Steering range, StrgRng Steering angle breakpoints, StrgAngBpts Steering ratio table, StrgRatioTbl

`Parametrized by` — Выберите параметризацию
`Lookup table` (значение по умолчанию) | `Constant`

Чтобы задать тип данных для рулевого механизма, используйте параметр Parametrized by.

Установка	Блокируйте реализацию
`Constant`	Рулевой механизм использует постоянные данные о параметре.
`Lookup table`	Рулевой механизм реализует таблицы для данных о параметре.

Зависимости

Эта таблица суммирует Type и зависимости от параметра Parametrized by.

Ввод	Параметрированный	Создает параметры
`Ackerman`	`Constant`	Track width, TrckWdth Wheel base, WhlBase Steering range, StrgRng Steering ratio, StrgRatio
`Ackerman`	`Lookup table`	Track width, TrckWdth Wheel base, WhlBase Steering range, StrgRng Steering angle breakpoints, StrgAngBpts Steering ratio table, StrgRatioTbl
`Rack and pinion`	`Constant`	Track width, TrckWdth Steering range, StrgRng Steering arm length, StrgArmLngth Rack casing length, RckCsLngth Tie rod length, TieRodLngth Distance between front axis and rack, D Pinion radius, PnnRadius
`Rack and pinion`	`Lookup table`	Track width, TrckWdth Steering range, StrgRng Steering angle breakpoints, StrgAngBpts Steering arm length, StrgArmLngth Rack casing length, RckCsLngth Tie rod length, TieRodLngth Distance between front axis and rack, D Pinion radius, PnnRadiusTbl
`Parallel`	`Constant`	Steering range, StrgRng Steering ratio, StrgRatio
`Parallel`	`Lookup table`	Steering range, StrgRng Steering angle breakpoints, StrgAngBpts Steering ratio table, StrgRatioTbl

`Power assist` — Укажите, что степень помогает
`on` (значение по умолчанию) | `off`

Если вы выбираете Power assist, можно указать, что крутящий момент помогает интерполяционной таблице, _ƒtrq, который является функцией скорости транспортного средства, v, и входного крутящего момента руля, _τin.

$τ_{a s t} = f_{t r q} (v, τ_{i n})$

Блок использует входной крутящий момент руля, и крутящий момент помогают вычислять держащуюся динамику.

Зависимости

Выбор Power assist создает VehSpd входной порт и эти параметры.

Степень помогает	Параметры
`on`	Steering wheel torque breakpoints, TrqBpts Vehicle speed breakpoints, VehSpdBpts Assisting torque table, TrqTbl Assisting torque limit, TrqLmt Assisting power limit, PwrLmt Assisting torque efficiency, Eta Cutoff frequency, omega_c

`Location` — Выберите местоположение
Front (значение по умолчанию) | Rear

Используйте параметр Location, чтобы задать переднее или заднее регулирование.

Установка	Реализация
Front	Переднее регулирование
Rear	Заднее регулирование

Установка

Реализация

Front

Переднее регулирование

Figure of front steering turning right

Rear

Заднее регулирование

Figure of rear steering turning right

Общий

`Track width, TrckWdth` width
1 | `scalar`

Ширина дорожки, TW, в m.

Зависимости

Чтобы создать этот параметр, установите Type на Ackerman или Rack and pinion.

`Wheel base, WhlBase` — Основа
1.524 (значение по умолчанию) | `scalar`

Основа колеса, WB, в m.

Зависимости

Чтобы создать этот параметр, установите Type на Ackerman.

`Steering range, StrgRng` Область значений
`1.25*pi` (значение по умолчанию) | `scalar`

Регулирование области значений, в рад. Блок ограничивает углы колеса, чтобы остаться в держащейся области значений.

`Steering ratio, StrgRatio` — Отношение
13.5 (значение по умолчанию) | `scalar`

Регулируя отношение, γ, безразмерный.

Зависимости

Создать этот параметр:

Установите Type на Ackerman или Parallel.
Установите Parametrized by на Constant.

`Steering angle breakpoints, StrgAngBpts` — Точки останова
[-6.2832 -5.0265 -3.7699 -2.5133 -1.2566 0 1.2566 2.5133 3.7699 5.0265 6.2832] (значение по умолчанию) | `vector`

Регулирование угловых точек останова, в рад.

Зависимости

Чтобы создать этот параметр, установите Parametrized by на Lookup table.

`Steering ratio table, StrgRatioTbl` Таблица
[13.5000 13.3750 13.2500 13.1250 13.0000 13.0000 13.0000 13.1250 13.2500 13.3750 13.5000] (значение по умолчанию) | `vector`

Регулируя таблицу отношения, γ, безразмерный.

Зависимости

Создать этот параметр:

Установите Type на Ackerman или Parallel.
Установите Parametrized by на Lookup table.

Реечный механизм

`Steering arm length, StrgArmLngth` длина
0.1 (значение по умолчанию) | `scalar`

Регулируя длину руки, _larm, в m.

Зависимости

Чтобы создать этот параметр, установите Type на Rack and pinion.

`Rack casing length, RckCsLngth` длина
0.5 (значение по умолчанию) | `scalar`

Установите в стойку случающуюся длину, _lrack, в m.

Зависимости

Чтобы создать этот параметр, установите Type на Rack and pinion.

`Tie rod length, TieRodLngth` длина
0.248 (значение по умолчанию) | `scalar`

Свяжите длину стержня, _lrod, в m.

Зависимости

Чтобы создать этот параметр, установите Type на Rack and pinion.

`Distance between front axis and rack, D` — Расстояние
0.2 (значение по умолчанию) | `scalar`

Расстояние между передней осью и стойкой, D, в m.

Зависимости

Чтобы создать этот параметр, установите Type на Rack and pinion.

`Pinion radius, PnnRadius` — Радиус
0.0057 (значение по умолчанию) | `scalar`

Свяжите радиус, r, в m.

Зависимости

Создать этот параметр:

Установите Type на Rack and pinion.
Установите Parametrized by на Constant.

`Pinion radius table, PnnRadiusTbl` Таблица
[0.0055 0.0055 0.0056 0.0057 0.0057 0.0057 0.0058 0.0057 0.0056 0.0055 0.0055] (значение по умолчанию) | `vector`

Свяжите таблицу радиуса, r, в m.

Зависимости

Создать этот параметр:

Установите Type на Rack and pinion.
Установите Parametrized by на Lookup table.

Динамика

`Steering wheel inertia, J1` — Инерция
0.1 (значение по умолчанию) | `scalar`

Инерция руля, _J1, в kg*m^2.

`Steering mechanism inertia, J2` — Инерция
0.01 (значение по умолчанию) | `scalar`

Инерция рулевого механизма, _J2, в kg*m^2.

`Upper hysteresis modifier, beta_u` — Верхний гистерезисный модификатор
0.1 (значение по умолчанию) | `scalar`

Верхний гистерезисный модификатор, _βu, безразмерный.

`Lower hysteresis modifier, beta_l` — Понизьте гистерезисный модификатор
0.1 (значение по умолчанию) | `scalar`

Понизьте гистерезисный модификатор, _βl, безразмерный.

`Hysteresis viscous damping, b1` — Затухание
0.001 (значение по умолчанию) | `scalar`

Гистерезисное затухание, _b1, в N · m·.

`Hysteresis stiffness, k1` — Жесткость
30 (значение по умолчанию) | `scalar`

Гистерезисная жесткость, _k1, в N · m/rad.

`Steering wheel damping, b2` — Затухание
1 (значение по умолчанию) | `scalar`

Затухание руля, _b2, в N · m·.

`Steering mechanism damping, b3` — Затухание
0.001 (значение по умолчанию) | `scalar`

Затухание рулевого механизма, _b3, в N · m·.

`Initial steering angle, theta_o` \angle
0 (значение по умолчанию) | `scalar`

Начальный руководящий угол, _θ0, в рад.

`Initial steering angular velocity, omega_o` — Скорость вращения
0 (значение по умолчанию) | `scalar`

Начальная руководящая скорость вращения, _ωo, в rad/s.

`Friction torque, FricTrq` — Крутящий момент
0 (значение по умолчанию) | `scalar`

Момент трения, _τfric, в N · m.

Степень помогает

`Steering wheel torque breakpoints, TrqBpts` — Точки останова
[-100 0 100] (значение по умолчанию) | `1`- `M` вектор

Точки останова крутящего момента руля, в N · m.

Зависимости

Выбор Power assist создает VehSpd входной порт и эти параметры.

Степень помогает	Параметры
`on`	Steering wheel torque breakpoints, TrqBpts Vehicle speed breakpoints, VehSpdBpts Assisting torque table, TrqTbl Assisting torque limit, TrqLmt Assisting power limit, PwrLmt Assisting torque efficiency, Eta Cutoff frequency, omega_c

`Vehicle speed breakpoints, VehSpdBpts` — Точки останова
[0 20] (значение по умолчанию) | `1`- `N` вектор

Точки останова скорости транспортного средства, в m/s.

Зависимости

Выбор Power assist создает VehSpd входной порт и эти параметры.

Степень помогает	Параметры
`on`	Steering wheel torque breakpoints, TrqBpts Vehicle speed breakpoints, VehSpdBpts Assisting torque table, TrqTbl Assisting torque limit, TrqLmt Assisting power limit, PwrLmt Assisting torque efficiency, Eta Cutoff frequency, omega_c

`Assisting torque table, TrqTbl` — 2D таблица крутящего момента
[0 -100;0 0;0 100] (значение по умолчанию) | `M`- `N` матрица

Помогая таблице крутящего момента, _ƒtrq, в N · m.

Крутящий момент помогает, интерполяционная таблица является функцией скорости транспортного средства, v, и входного крутящего момента руля, _τin.

$τ_{a s t} = f_{t r q} (v, τ_{i n})$

Блок использует входной крутящий момент руля, и крутящий момент помогают вычислять держащуюся динамику.

Зависимости

Выбор Power assist создает VehSpd входной порт и эти параметры.

Степень помогает	Параметры
`on`	Steering wheel torque breakpoints, TrqBpts Vehicle speed breakpoints, VehSpdBpts Assisting torque table, TrqTbl Assisting torque limit, TrqLmt Assisting power limit, PwrLmt Assisting torque efficiency, Eta Cutoff frequency, omega_c

`Assisting torque limit, TrqLmt` — Закрутите предел
100 (значение по умолчанию) | `scalar`

Помощь пределу крутящего момента, в N · m.

Зависимости

Выбор Power assist создает VehSpd входной порт и эти параметры.

Степень помогает	Параметры
`on`	Steering wheel torque breakpoints, TrqBpts Vehicle speed breakpoints, VehSpdBpts Assisting torque table, TrqTbl Assisting torque limit, TrqLmt Assisting power limit, PwrLmt Assisting torque efficiency, Eta Cutoff frequency, omega_c

`Assisting power limit, PwrLmt` — Предел степени
1000 (значение по умолчанию) | `scalar`

Помощь пределу степени, в N · m/s.

Зависимости

Выбор Power assist создает VehSpd входной порт и эти параметры.

Степень помогает	Параметры
`on`	Steering wheel torque breakpoints, TrqBpts Vehicle speed breakpoints, VehSpdBpts Assisting torque table, TrqTbl Assisting torque limit, TrqLmt Assisting power limit, PwrLmt Assisting torque efficiency, Eta Cutoff frequency, omega_c

`Assisting torque efficiency, Eta` Эффективность
1 (значение по умолчанию) | `scalar`

Помощь КПД крутящего момента, безразмерному.

Зависимости

Выбор Power assist создает VehSpd входной порт и эти параметры.

Степень помогает	Параметры
`on`	Steering wheel torque breakpoints, TrqBpts Vehicle speed breakpoints, VehSpdBpts Assisting torque table, TrqTbl Assisting torque limit, TrqLmt Assisting power limit, PwrLmt Assisting torque efficiency, Eta Cutoff frequency, omega_c

`Cutoff frequency, omega_c` — Частота среза
200 (значение по умолчанию) | `scalar`

Частота среза, в rad/s.

Зависимости

Выбор Power assist создает VehSpd входной порт и эти параметры.

Степень помогает	Параметры
`on`	Steering wheel torque breakpoints, TrqBpts Vehicle speed breakpoints, VehSpdBpts Assisting torque table, TrqTbl Assisting torque limit, TrqLmt Assisting power limit, PwrLmt Assisting torque efficiency, Eta Cutoff frequency, omega_c

Ссылки

[1] Crolla, Дэвид, Дэвид Фостер, и др. Энциклопедия Автомобильной Разработки. Объем 4, Часть 5 (Системы Шасси) и Часть 6 (Электрические и Электронные системы). Чичестер, Западный Сассекс, Соединенное Королевство: John Wiley & Sons Ltd, 2015.

[2] Гиллеспи, Томас. Основные принципы динамики аппарата. Варрендэйл, усилитель мощности (УМ): ассоциация инженеров автомобилестроения, 1992.

[3] Комитет по стандартам динамики аппарата. Терминология динамики аппарата. SAE J670. Варрендэйл, усилитель мощности (УМ): ассоциация инженеров автомобилестроения, 2008.

Расширенные возможности

Генерация кода C/C++
Генерация кода C и C++ с помощью Simulink® Coder™.

Смотрите также

Kinematic Steering | Mapped Steering

Темы

Системы координат в Vehicle Dynamics Blockset

Введенный в R2018a

Документация

Dynamic Steering

Описание

Динамика

Регулирование типов

Порты

Входной параметр

TrqIn — Крутящий момент scalar

TrqLft — Оставленный крутящий момент колеса scalar

TrqRght — Правильный крутящий момент колеса scalar

VehSpd — Скорость транспортного средства scalar

Зависимости

Вывод

Info — Сигнал шины шина

AngLft — Оставленный угол колеса scalar

AngRght — Правильный угол колеса scalar

Параметры

Type — Выберите держащийся тип Rack and pinion (значение по умолчанию) | Ackerman | Parallel

Зависимости

Parametrized by — Выберите параметризацию Lookup table (значение по умолчанию) | Constant

Зависимости

Power assist — Укажите, что степень помогает on (значение по умолчанию) | off

Зависимости

Location — Выберите местоположение Front (значение по умолчанию) | Rear

Track width, TrckWdth width1 | scalar

Зависимости

Wheel base, WhlBase — Основа1.524 (значение по умолчанию) | scalar

Зависимости

Steering range, StrgRng Область значений 1.25*pi (значение по умолчанию) | scalar

Steering ratio, StrgRatio — Отношение13.5 (значение по умолчанию) | scalar

Зависимости

Steering angle breakpoints, StrgAngBpts — Точки останова[-6.2832 -5.0265 -3.7699 -2.5133 -1.2566 0 1.2566 2.5133 3.7699 5.0265 6.2832] (значение по умолчанию) | vector

Зависимости

Steering ratio table, StrgRatioTbl Таблица[13.5000 13.3750 13.2500 13.1250 13.0000 13.0000 13.0000 13.1250 13.2500 13.3750 13.5000] (значение по умолчанию) | vector

Зависимости

Steering arm length, StrgArmLngth длина0.1 (значение по умолчанию) | scalar

Зависимости

Rack casing length, RckCsLngth длина0.5 (значение по умолчанию) | scalar

Зависимости

Tie rod length, TieRodLngth длина0.248 (значение по умолчанию) | scalar

Зависимости

Distance between front axis and rack, D — Расстояние0.2 (значение по умолчанию) | scalar

Зависимости

Pinion radius, PnnRadius — Радиус0.0057 (значение по умолчанию) | scalar

Зависимости

Pinion radius table, PnnRadiusTbl Таблица[0.0055 0.0055 0.0056 0.0057 0.0057 0.0057 0.0058 0.0057 0.0056 0.0055 0.0055] (значение по умолчанию) | vector

Зависимости

Steering wheel inertia, J1 — Инерция0.1 (значение по умолчанию) | scalar

Steering mechanism inertia, J2 — Инерция0.01 (значение по умолчанию) | scalar

Upper hysteresis modifier, beta_u — Верхний гистерезисный модификатор0.1 (значение по умолчанию) | scalar

Lower hysteresis modifier, beta_l — Понизьте гистерезисный модификатор0.1 (значение по умолчанию) | scalar

Hysteresis viscous damping, b1 — Затухание0.001 (значение по умолчанию) | scalar

Hysteresis stiffness, k1 — Жесткость30 (значение по умолчанию) | scalar

Steering wheel damping, b2 — Затухание1 (значение по умолчанию) | scalar

Steering mechanism damping, b3 — Затухание0.001 (значение по умолчанию) | scalar

Initial steering angle, theta_o \angle0 (значение по умолчанию) | scalar

Initial steering angular velocity, omega_o — Скорость вращения0 (значение по умолчанию) | scalar

Friction torque, FricTrq — Крутящий момент0 (значение по умолчанию) | scalar

Steering wheel torque breakpoints, TrqBpts — Точки останова[-100 0 100] (значение по умолчанию) | 1- M вектор

Зависимости

Vehicle speed breakpoints, VehSpdBpts — Точки останова[0 20] (значение по умолчанию) | 1- N вектор

Зависимости

Assisting torque table, TrqTbl — 2D таблица крутящего момента[0 -100;0 0;0 100] (значение по умолчанию) | M- N матрица

Зависимости

Assisting torque limit, TrqLmt — Закрутите предел100 (значение по умолчанию) | scalar

Зависимости

Assisting power limit, PwrLmt — Предел степени1000 (значение по умолчанию) | scalar

Зависимости

Assisting torque efficiency, Eta Эффективность1 (значение по умолчанию) | scalar

Зависимости

Cutoff frequency, omega_c — Частота среза200 (значение по умолчанию) | scalar

Зависимости

Ссылки

Расширенные возможности

Генерация кода C/C++ Генерация кода C и C++ с помощью Simulink® Coder™.

Смотрите также

Темы

Документация Vehicle Dynamics Blockset

Поддержка

`TrqIn` — Крутящий момент
`scalar`

`TrqLft` — Оставленный крутящий момент колеса
`scalar`

`TrqRght` — Правильный крутящий момент колеса
`scalar`

`VehSpd` — Скорость транспортного средства
`scalar`

`Info` — Сигнал шины
шина

`AngLft` — Оставленный угол колеса
`scalar`

`AngRght` — Правильный угол колеса
`scalar`

`Type` — Выберите держащийся тип
`Rack and pinion` (значение по умолчанию) | `Ackerman` | `Parallel`

`Parametrized by` — Выберите параметризацию
`Lookup table` (значение по умолчанию) | `Constant`

`Power assist` — Укажите, что степень помогает
`on` (значение по умолчанию) | `off`

`Location` — Выберите местоположение
Front (значение по умолчанию) | Rear

`Track width, TrckWdth` width
1 | `scalar`

`Wheel base, WhlBase` — Основа
1.524 (значение по умолчанию) | `scalar`

`Steering range, StrgRng` Область значений
`1.25*pi` (значение по умолчанию) | `scalar`

`Steering ratio, StrgRatio` — Отношение
13.5 (значение по умолчанию) | `scalar`

`Steering angle breakpoints, StrgAngBpts` — Точки останова
[-6.2832 -5.0265 -3.7699 -2.5133 -1.2566 0 1.2566 2.5133 3.7699 5.0265 6.2832] (значение по умолчанию) | `vector`

`Steering ratio table, StrgRatioTbl` Таблица
[13.5000 13.3750 13.2500 13.1250 13.0000 13.0000 13.0000 13.1250 13.2500 13.3750 13.5000] (значение по умолчанию) | `vector`

`Steering arm length, StrgArmLngth` длина
0.1 (значение по умолчанию) | `scalar`

`Rack casing length, RckCsLngth` длина
0.5 (значение по умолчанию) | `scalar`

`Tie rod length, TieRodLngth` длина
0.248 (значение по умолчанию) | `scalar`

`Distance between front axis and rack, D` — Расстояние
0.2 (значение по умолчанию) | `scalar`

`Pinion radius, PnnRadius` — Радиус
0.0057 (значение по умолчанию) | `scalar`

`Pinion radius table, PnnRadiusTbl` Таблица
[0.0055 0.0055 0.0056 0.0057 0.0057 0.0057 0.0058 0.0057 0.0056 0.0055 0.0055] (значение по умолчанию) | `vector`

`Steering wheel inertia, J1` — Инерция
0.1 (значение по умолчанию) | `scalar`

`Steering mechanism inertia, J2` — Инерция
0.01 (значение по умолчанию) | `scalar`

`Upper hysteresis modifier, beta_u` — Верхний гистерезисный модификатор
0.1 (значение по умолчанию) | `scalar`

`Lower hysteresis modifier, beta_l` — Понизьте гистерезисный модификатор
0.1 (значение по умолчанию) | `scalar`

`Hysteresis viscous damping, b1` — Затухание
0.001 (значение по умолчанию) | `scalar`

`Hysteresis stiffness, k1` — Жесткость
30 (значение по умолчанию) | `scalar`

`Steering wheel damping, b2` — Затухание
1 (значение по умолчанию) | `scalar`

`Steering mechanism damping, b3` — Затухание
0.001 (значение по умолчанию) | `scalar`

`Initial steering angle, theta_o` \angle
0 (значение по умолчанию) | `scalar`

`Initial steering angular velocity, omega_o` — Скорость вращения
0 (значение по умолчанию) | `scalar`

`Friction torque, FricTrq` — Крутящий момент
0 (значение по умолчанию) | `scalar`

`Steering wheel torque breakpoints, TrqBpts` — Точки останова
[-100 0 100] (значение по умолчанию) | `1`- `M` вектор

`Vehicle speed breakpoints, VehSpdBpts` — Точки останова
[0 20] (значение по умолчанию) | `1`- `N` вектор

`Assisting torque table, TrqTbl` — 2D таблица крутящего момента
[0 -100;0 0;0 100] (значение по умолчанию) | `M`- `N` матрица

`Assisting torque limit, TrqLmt` — Закрутите предел
100 (значение по умолчанию) | `scalar`

`Assisting power limit, PwrLmt` — Предел степени
1000 (значение по умолчанию) | `scalar`

`Assisting torque efficiency, Eta` Эффективность
1 (значение по умолчанию) | `scalar`

`Cutoff frequency, omega_c` — Частота среза
200 (значение по умолчанию) | `scalar`

Генерация кода C/C++
Генерация кода C и C++ с помощью Simulink® Coder™.