Конечное воздействие проводимости и толщины в решателе MoM

Antenna Toolbox™ использует метод расчета метода моментов (MoM) для конечных металлических диэлектрических антенн. Метод MoM предоставляет вычислительное решение электромагнитных проблем путем дискретизации Уравнений Максвелла. Процесс приводит к этой матрично-векторной системе:

$V = ZI$

где,

V— Прикладной вектор напряжения. Этот сигнал может быть напряжением, или степень применилась к антенне или инцидентному сигналу, падающему на антенну.
Я — Текущий вектор, который представляет текущий на поверхности антенны.
Z Матрица взаимодействия или матрица импеданса, которая имеет отношение V ко мне. Для получения дополнительной информации о матрице взаимодействия см. Метод Решателя Моментов для Металлических и Диэлектрических Структур.

В металлах совершенного электрически проведения (PEC) электрическая проводимость бесконечна, и толщина принята, чтобы быть бесконечно тонкой. Поэтому эффект кожи не рассматривается в металлической антенне PEC. Однако в антеннах металла наиболее практического применения, металлический лист имеет конечную проводимость и конечную толщину. Это вызывает формирование конечного воздействия глубины кожи, которое обычно характеризуется эквивалентным поверхностным импедансом [1].

Antenna Toolbox использует метод MoM [2], чтобы решить конечные металлические антенны, где конечная проводимость и толщина металла рассматриваются через эквивалентную поверхность. Таким образом, по сравнению с металлом PEC, нет никакого изменения в вычислительное время и сцепляющийся в non-PEC металлических антеннах. Базовая электромагнитная теория моделирования конечного проводника объяснена ниже.

Рассмотрите металлический лист с конечными размерностями в свободном пространстве как показано в рисунке 1.

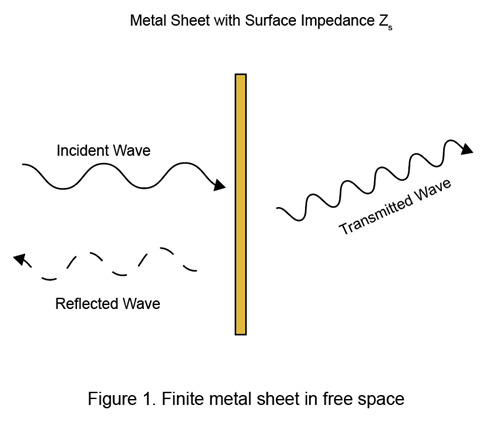
Finite metal sheet with surface impedance, Zs in free space

Используя моделирование линии электропередачи, его представление эквивалентной схемы моделируется с эквивалентным поверхностным импедансом _Zs. Это показывают в рисунке 2.

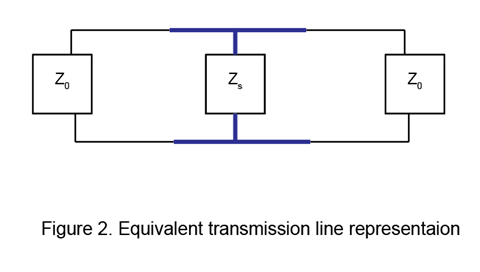
Equivalent transmission line model with surface impedance, Zs.

Конечная проводимость излагает помеху для эквивалентного поверхностного электрического тока на поверхности антенны. После полевого отношения непрерывности на проводниковой поверхности смоделируйте конечную проводимость с помощью эквивалентного поверхностного импеданса. Эквивалентный поверхностный импеданс _Zs может быть записан с помощью [1] как

$\begin{array}{l} Z_{s} = \frac{k_{c}}{σ_{c}} (\frac{\exp (k_{c} t) + \frac{σ_{c} Z_{0} - k_{c}}{σ_{c} Z_{0} {+k}_{c}} \exp (- k_{c} t)}{\exp (k_{c} t) - \frac{σ_{c} Z_{0} - k_{c}}{σ_{c} Z_{0} {+k}_{c}} \exp (- k_{c} t)}) \\ где, \\ t - толщина металла \\ σ_{c} - проводимость металла \\ Z_{0} = \sqrt{\frac{μ}{ε}}, импеданс внутреннего параметра свободного пространства \\ k_{c} = \frac{1+j}{δ_{c}} \\ δ_{c} = \sqrt{\frac{2}{ω μ σ_{c}}} = \sqrt{\frac{1}{π f μ σ_{c}}}, глубина кожи \end{array}$

Глубина параметра кожи, физически имеет значение, насколько поверхностный ток может проникнуть поверхность проведения. Для металлов PEC глубина кожи является нулем, когда проводимость бесконечна. Таким образом целое распределение тока находится по поверхностному слою в металлах PEC. Для non-PEC металлов, если значение глубины кожи является очень низким, exp _(kct) имеет тенденцию быть очень высоким. В случаях наиболее практического применения проводимость очень высока и поэтому, _Z0>> _kc/σc. В таком случае _Zs становится:

$Z_{s} = \frac{k_{c}}{σ_{c}} (\frac{1 + \exp (k_{c} t)}{1 - \exp (k_{c} t)})$

Если толщина высока, exp _(-2kct) имеет тенденцию быть незначительным, и _Zs становится:

$Z_{s} = \frac{k_{c}}{σ_{c}} = (1 + j) \sqrt{\frac{ω μ}{2 σ_{c}}}$

Таким образом, для металлов с высокими значениями проводимости и толщины, поверхностный импеданс становится независимым от толщины.

Формулировка MoM

В конечных металлически-диэлектрических структурах элементы матрицы взаимодействия от металла к металлу вычисляются, как дали в [2] и [3].

$Z_{m n}^{M M} = (\frac{j ω μ}{4 π}) \int_{s} \int_{s'} \vec{f_{m}^{M}} (\vec{r}) . \vec{f_{n}^{M}} (\vec{r'}) {\vec{g d r}}^{'} \vec{d r} - \frac{j}{4 π ω ε} \int_{s} \int_{s'} \vec{\nabla f_{m}^{M}} (\vec{r}) . \vec{\nabla f_{n}^{M}} (\vec{r'}) {\vec{g d r}}^{'} \vec{d r} + Z_{s} \int_{s} \vec{f_{m}^{M}} (\vec{r}) . \vec{f_{n}^{M}} (\vec{r'}) \vec{d r}$

Первые два термина в уравнении рассматривают электрический скалярный потенциал и магнитный вектор-потенциал электромагнитных полей. Третий термин рассматривает конечное поверхностное воздействие импеданса из-за ненулевой глубины кожи конечных металлических антенн. В антеннах PEC, _Zs = 0; таким образом никакая конечная потеря проводимости не происходит в металлах PEC. Рао-Вилтон-Глиссон (RWG) [4] основные функции в уравнении MoM используется. Для получения дополнительной информации см. Метод Решателя Моментов для Металлических и Диэлектрических Структур.

Ссылки

[1] А. Керр. "Поверхностный импеданс сверхпроводников и нормальных проводников в средствах моделирования EM". Записка MMA, издание 21, № 245, стр 1-17, 1999.

[2] Sarkar, T.K., и Э. Арвас. “Подход Интегрального уравнения к Анализу Конечных Микрополосковых Антенн: Формулировка объема/Поверхности”. Транзакции IEEE на Антеннах и Распространении 38, № 3 (март 1990): 305–12. https://doi.org/10.1109/8.52238.

[3] Rengarajan, Сембиэм Рэджэгопэл и Ричард Э. Ходжес. “Точная Оценка Проводниковой Потери в Прямоугольной Микрополосковой Закрашенной фигуре Reﬂectarrays”. Прогресс исследования M 75 Электромагнетизма (2018): 159–66. https://doi.org/10.2528/PIERM18072606.

[4] Рао, S. D. Вильтон и А. Глиссон. “Электромагнитное Рассеивание Поверхностями Произвольной Формы”. Транзакции IEEE на Антеннах и Распространении 30, № 3 (май 1982): 409–18. https://doi.org/10.1109/TAP.1982.1142818.

Документация