Трассировка лучей для радиосвязей

Введение

Системы радиосвязи используют радиоволны для передаваемых сигналов. Моделирование распространения позволяет вам оценить силу сигналов на основе системных параметров, таких как частота, высота антенны, свойства ландшафта и свойства создания.

Теоретические и эмпирические модели оценивают потерю на пути на основе области значений и допустимы только для тех сред, которые напоминают среду моделирования. В результате они обычно не предоставляют точную временную или пространственную информацию. В отличие от этих моделей, модели трассировки лучей характерны для 3-D среды и поэтому подходят для сценариев, таких как городские среды.

Для моделирования распространения ray является отдельным сигналом радио что [1]:

Перемещения в прямой линии через гомогенный носитель.
Подчиняется законам отражения, преломления и дифракции.
Несет энергию. Модели распространения обрабатывают лучи как трубы, где плотность энергии на сечении становится меньшей, когда луч взаимодействует со средой.

Для данной 3-D среды модели трассировки лучей используют числовые симуляции для:

Предскажите пути лучей с передатчиков на приемники. Модели могут найти много лучей с передатчика на приемник. Модели выводят угол отъезда, угол прибытия и время прибытия от путей.
Оцените потерю на пути и фазовый переход для каждого луча. Общая потеря на пути является суммой потерь взаимодействия, потери свободного пространства, и, опционально, атмосферной потери.

Луч взаимодействует со средой несколькими способами [1].

Взаимодействие	Описание
Угол обзора (LOS)	Луч перемещается непосредственно от передатчика к приемнику.
Отражение	Луч отражается от поверхности согласно закону отражения.
Преломление (передача)	Луч преломляет, когда он перемещается в новый носитель, согласно закону преломления.
Дифракция	Луч дифрагировал от поверхности согласно закону дифракции. Один луч может породить много дифрагированных лучей.
Рассеивание	Луч взаимодействует с грубой поверхностью, такой как океан или фасад здания.

Используйте эти функции, чтобы создать модели трассировки лучей, предсказать пути к распространению и вычислить сдвиги фазы и потери на пути.

propagationModel — Создайте модель трассировки лучей как RayTracing объект. Задайте опции, такие как метод трассировки лучей, максимальное количество отражений и поверхностные материалы. Можно использовать модели трассировки лучей в качестве входа при способствовании анализа RF, такой, генерируя карты покрытия при помощи coverage функционируйте или при вычислении общей мощности приемника при помощи sigstrength функция.
raytrace — Отобразите пути к распространению (лучи) на карте или возвратите пути к распространению как comm.Ray объекты. Каждый объект представляет полный путь от передатчика к приемнику и содержит информацию, такую как потеря на пути, сдвиг фазы и типы поверхностных взаимодействий.
raypl — Вычислите потерю на пути и сдвиг фазы для пути к распространению на основе поверхностных материалов и типов поляризации антенны.

Для примеров, которые показывают трассировку лучей во внутренних и городских средах, смотрите, что Внутренняя Линия связи MIMO-OFDM Использует Трассировку лучей и Городскую Ссылку и Анализ покрытия Используя Трассировку лучей, соответственно.

Методы трассировки лучей

Модель трассировки лучей, используемая propagationModel и raytrace функции находят пути к не углу обзора (NLOS) и LOS.

Модель находит пути к LOS путем стрельбы в луч от передатчика к приемнику. Если луч не взаимодействует с поверхностью прежде, чем достигнуть приемника, то путь к LOS существует.
Модель находит пути NLOS или при помощи стрельбы и возврата лучей (SBR) метод [2] или при помощи метода изображений. Можно задать метод при помощи propagationModel функция.

Выберите метод на основе типов взаимодействий, которые вы хотите смоделировать, скорость расчета и точность.

Метод	Типы взаимодействия	Скорость расчета	Точность расчета
SBR	Включает эффекты от отражения и не включает эффекты от дифракции, преломления или рассеивания. Вычисление поддержек аппроксимированных путей к распространению максимум для десяти отражений пути.	Вычислительная сложность увеличивается линейно с количеством отражений. В результате метод SBR обычно быстрее, чем метод изображений.	Местоположения сайтов приемника, вычисленных методом SBR, не точны. Точность расчетных путей к распространению уменьшается как продолжительность увеличений путей.
Изображение	Включает эффекты от отражения и не включает эффекты от дифракции, преломления или рассеивания. Поддержки до двух отражений пути.	Вычислительная сложность увеличивается экспоненциально с количеством отражений.	Вычисляет точные пути к распространению.

Метод

Типы взаимодействия

Скорость расчета

Точность расчета

SBR

Включает эффекты от отражения и не включает эффекты от дифракции, преломления или рассеивания.

Вычисление поддержек аппроксимированных путей к распространению максимум для десяти отражений пути.

Вычислительная сложность увеличивается линейно с количеством отражений. В результате метод SBR обычно быстрее, чем метод изображений.

Местоположения сайтов приемника, вычисленных методом SBR, не точны. Точность расчетных путей к распространению уменьшается как продолжительность увеличений путей.

Изображение

Включает эффекты от отражения и не включает эффекты от дифракции, преломления или рассеивания.

Поддержки до двух отражений пути.

Вычислительная сложность увеличивается экспоненциально с количеством отражений.

Вычисляет точные пути к распространению.

Метод SBR

Этот рисунок иллюстрирует метод SBR для вычисления путей к распространению от передатчика, Tx, к приемнику, Rx.

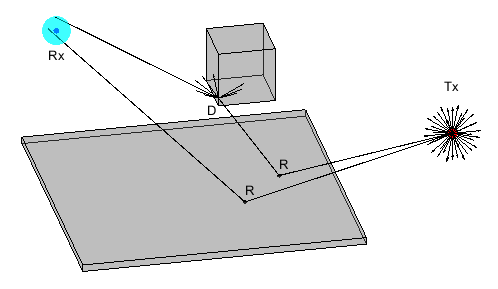
$Ray tracing reflection and diffraction using the SBR method$

Метод SBR запускает много лучей от геодезической сферы, сосредоточенной в Tx. Геодезическая сфера позволяет модели запустить лучи, которые приблизительно расположены равными интервалами.

Затем метод прослеживает каждый луч от Tx и может смоделировать различные типы взаимодействий между лучами и окружающими объектами, такими как отражения, дифракции, преломления и рассеивание. Обратите внимание на то, что реализация рассматривает только отражения.

Когда луч поражает плоскую поверхность, показавшую R, луч отражается на основе закона отражения.
Когда луч поражает ребро, показавшее D, луч порождает много дифрагированных лучей на основе закона дифракции [3][4]. Каждый дифрагированный луч имеет тот же угол с ребром дифрагирования как инцидентный луч. Дифракционная точка затем становится новой стартовой точкой, и метод SBR прослеживает дифрагированные лучи таким же образом как лучи, запущенные от Tx. Континуум дифрагированных лучей формирует конус вокруг ребра дифрагирования, которое обычно известно как Keller cone [4]. Текущая реализация метода SBR не рассматривает дифракцию.

Для каждого запущенного луча метод окружает Rx сферой, названной сферой приема, радиусом, который пропорционален угловому разделению запущенных лучей и расстояния перемещения луча. Если луч пересекает сферу, то модель считает луч допустимым путем от Tx до Rx.

Отобразите метод

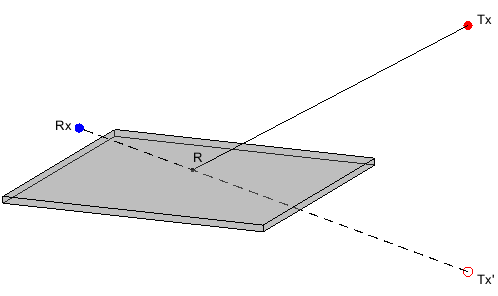
Этот рисунок иллюстрирует метод изображений для вычисления пути к распространению одного отражательного луча для того же передатчика и приемника как метод SBR. Метод изображений определяет местоположение изображения Tx относительно плоской отражательной поверхности, Tx'. Затем метод соединяет Tx' и Rx с линейным сегментом. Если линейный сегмент пересекает плоскую отражательную поверхность, показавшую R на рисунке, то допустимый путь от Tx до Rx существует. Метод определяет пути с несколькими отражениями путем рекурсивного расширения этих шагов.

Ray tracing using the image method

Потеря распространения

Модель трассировки лучей, используемая propagationModel, raytrace, и raypl функции вычисляют отражательные потери путем отслеживания горизонтальной и вертикальной поляризации сигналов через путь к распространению. Общие потери мощности являются суммой потери свободного пространства и отражательной потери.

Эффект поверхностных материалов

Когда луч взаимодействует с поверхностью, поверхностный материал влияет на отражательные потери.

Модель трассировки лучей включает создание и поверхностные материалы в вычисления распространения потерь при помощи комплексной относительной проницаемости поверхности, _εr. ITU-R P.2040-1 [5] и рекомендации ITU-R P.527 [6] включают методы, уравнения, и значения раньше вычисляли _εr для области значений частот.

Уравнения для _εr:

$ε_{r} = ε_{r}^{'} + j ε_{r}^{' '}$

$ε_{r}^{' '} = \frac{σ}{2 π ε_{0} f}$ ,

где:

_εr' является действительной относительной проницаемостью.
σ является проводимостью в S/m.
_ε0 является проницаемостью свободного пространства (электрическая константа).
f является частотой в Гц.

Для строительных материалов модель трассировки лучей вычисляет _εr' и σ как:

$ε_{r}^{'} = a f^{b}$

$σ = c f^{d}$ ,

где a, b, c и d являются константами, определенными поверхностным материалом. Для удобочитаемости таблица показывает частотный диапазон в GHz.

Материальный класс	Действительная часть относительной проницаемости		Проводимость (S/m)		Частотный диапазон (GHz)
Материальный класс	a	b	c	d	Частотный диапазон (GHz)
Вакуум (~ воздух)	1	0	0	0	[0.001, 100]
Бетон	5.31	0	0.0326	0.8095	[1, 100]
Кирпич	3.75	0	0.038	0	[1, 10]
Гипсокартон	2.94	0	0.0116	0.7076	[1, 100]
Древесина	1.99	0	0.0047	1.0718	[0.001, 100]
Стекло	6.27	0	0.0043	1.1925	[0.1, 100]
Потолок платы	1.50	0	0.0005	1.1634	[1, 100]
Плата с микросхемами	2.58	0	0.0217	0.78	[1, 100]
Половица	3.66	0	0.0044	1.3515	[50, 100]
Металл	1	0	10⁷	0	[1, 100]
Очень сухая земля	3	0	0.00015	2.52	[1, 10] только^(a)
Носитель сушит землю	15	– 0.1	0.035	1.63	[1, 10] только^(a)
Влажная земля	30	– 0.4	0.15	1.30	[1, 10] только^(a)
Примечание (a): Для трех наземных типов (очень сухой, средний сухой, и влажный), не могут быть превышены отмеченные пределы частоты.

Для наземных поверхностей, таких как вода, морская вода, сухой или влажный лед, сухая или влажная почва и растительность, модель трассировки лучей вычисляет _εr с помощью методов и уравнений, представленных в ITU-R P.527 [6].

Отражательная потеря

Модель трассировки лучей вычисляет отражательную потерю при помощи отражательных матричных расчетов, описанных в документе IEEE 802.11-09/0334r8 [7].

Это изображение показывает отражательный путь от ретранслятора Tx на сайт приемника Rx.

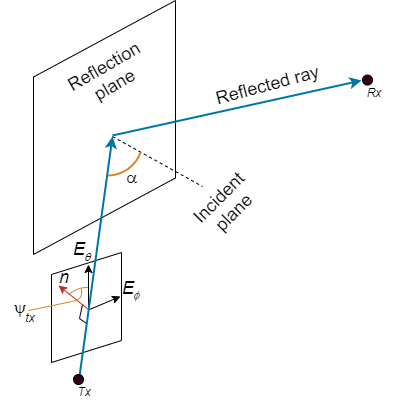
Reflection path from a transmitter site to a receiver site

Поскольку первый порядок сигнализирует об отражении, уравнение для отражательной потери на пути, _PLR:

$P L_{R} = J V_{r x}^{'} H_{r e f 1} J V_{t x}$ ,

где:

_JVrx и _JVtx являются 2 1 векторами поляризации для приемника и передатчика в виде векторов Джонса.
_Href1 является отражательной матрицей.

Уравнение для отражательного матричного _Href1:

$H_{r e f 1} = (\begin{matrix} \cos (Ψ_{r x}) & \sin (Ψ_{r x}) \\ - \sin (Ψ_{r x}) & \cos (Ψ_{r x}) \end{matrix}) \times (\begin{matrix} R_{⊥} (α) & 0 \\ 0 & R_{∥} (α) \end{matrix}) \times (\begin{matrix} \cos (Ψ_{t x}) & \sin (Ψ_{t x}) \\ - \sin (Ψ_{t x}) & \cos (Ψ_{t x}) \end{matrix})$ ,

где:

Третьи и первые термины являются геометрическими матрицами связи. Третий термин повторно вычисляет вектор поляризации от базиса координат передатчика к базису инцидентной плоскости. Первый термин повторно вычисляет вектор поляризации от базиса инцидентной плоскости к базису координат приемника. _Ψrx и _Ψtx являются углами между вертикальным вектором электромагнитного поля _Eθ и нормальным к инцидентной плоскости, n, в приемнике и передатчике, соответственно.
Второй термин является матрицей поляризации, где _R∥ и _R⟂ являются отражательными коэффициентами для горизонтальной и вертикальной поляризации, соответственно.

Модель составляет геометрическую связь между горизонтальной и вертикальной поляризацией только, когда и антенны передатчика и приемника поляризованы.

Модели трассировки лучей вычисляют _R∥ и _R⟂ при помощи Уравнения Френеля:

$R_{∥} (α) = \frac{\cos (α) - \sqrt{ε_{r} - \sin^{2} (α)}}{\cos (α) + \sqrt{ε_{r} - \sin^{2} (α)}}$

$R_{⊥} (α) = \frac{\cos (α) - \sqrt{(ε_{r} - \sin^{2} (α)) / ε_{r}^{2}}}{\cos (α) + \sqrt{(ε_{r} - \sin^{2} (α)) / ε_{r}^{2}}}$ ,

где:

α является инцидентным углом вектора распространения.
_εr является комплексной относительной проницаемостью материала.

Модель вычисляет отражения высшего порядка при помощи дополнительной геометрической матрицы связи и матрицы поляризации для каждого отражения.

Ссылки

[1] Юнь, Zhengqing и Магды Ф. Искандер. “Трассировка лучей для Радио-Моделирования Распространения: Принципы и Приложения”. IEEE доступ 3 (2015): 1089–1100. https://doi.org/10.1109/ACCESS.2015.2453991.

[2] Schaubach, K.R., Нью-Джерси Дэвис и Т.С. Рэппэпорт. “Метод Трассировки лучей для Предсказания Потери на пути и Распространения Задержки в Микросотовых Средах”. В [1 992 Продолжения] Автомобильное Технологическое Общество 42-я Конференция VTS - Границы Технологии, 932–35. Denver, CO, США: IEEE, 1992. https://doi.org/10.1109/VETEC.1992.245274.

[3] Сектор Радиосвязи Международного союза электросвязи. Распространение дифракцией. Рекомендация P.526-15. ITU-R, утвержденный 21 октября 2019. https://www.itu.int/rec/R-REC-P.526-15-201910-I/en.

[4] Келлер, Джозеф Б. “Геометрическая Теория Дифракции”. Журнал Оптического Общества Америки 52, № 2 (1 февраля 1962): 116. https://doi.org/10.1364/JOSA.52.000116.

[5] Сектор Радиосвязи Международного союза электросвязи. Эффекты строительных материалов и структур на распространении радиоволны выше приблизительно 100 МГц. Рекомендация P.2040-1. ITU-R, утвержденный 29 июля 2015. https://www.itu.int/rec/R-REC-P.2040-1-201507-I/en.

[6] Сектор Радиосвязи Международного союза электросвязи. Электрические характеристики поверхности Земли. Рекомендация P.527-5. ITU-R, утвержденный 14 августа 2019. https://www.itu.int/rec/R-REC-P.527-5-201908-I/en.

[7] Малцев, A., и др. "Модели канала для 60 систем GHz WLAN". Документ IEEE 802.11-09/0334r8, май 2010.

[8] Макнамара, D. A. К. В. Ай. Писториус и Дж. А. Г. Мэлэрб. Введение в универсальную геометрическую теорию дифракции. Бостон: дом Artech, 1990.

Смотрите также

Функции

propagationModel | raytrace | raypl | buildingMaterialPermittivity | earthSurfacePermittivity

Объекты

RayTracing | comm.Ray

Документация