kalman

Спроектируйте Фильтр Калмана для оценки состояния

свернуть все на странице

Синтаксис

[kalmf,L,P] = kalman(sys,Q,R,N)

[kalmf,L,P] = kalman(sys,Q,R,N,sensors,known)

[kalmf,L,P,Mx,Z,My] = kalman(___)

[kalmf,L,P,Mx,Z,My] = kalman(___,type)

Описание

пример

[kalmf,L,P] = kalman(sys,Q,R,N) создает Фильтр Калмана, учитывая модель объекта управления sys и шумовые данные о ковариации QR, и N. Функция вычисляет Фильтр Калмана для использования в Оценке состояния фильтра Калмана с настройкой, показанной в следующей схеме.

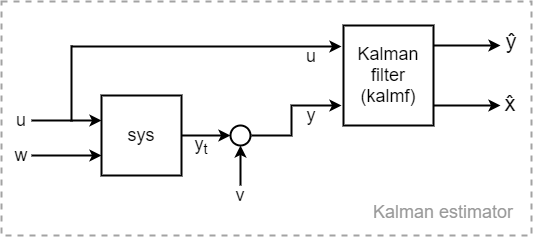
Kalman estimator including plant sys and Kalman filter kalmf. The plant has input u, noise input w, and output yt. The Kalman filter takes as inputs w and noisy plant output y = yt + v. The filter outputs are y-hat, the estimated true plant output, and x-hat, the estimated state values.

Вы создаете модель sys с известными входными параметрами u и белый шум процесса вводит w, такой, что w состоит из последних входных параметров _Nw к sys. "Истинный" объект выход _yt состоит из всех выходных параметров sys. Вы также предоставляете шумовым данным о ковариации QR, и N. Возвращенный Фильтр Калмана kalmf модель в пространстве состояний, которая берет известные входные параметры u и шумные измерения y и производит оценку $\hat{y}$ из истинного объекта выход и оценка $\hat{x}$ из состояний объекта. kalman также возвращается, Кальман получает L и установившаяся ошибочная ковариационная матрица P.

пример

[kalmf,L,P] = kalman(sys,Q,R,N,sensors,known) вычисляет Фильтр Калмана, когда один или оба из следующих условий существуют.

Не все выходные параметры sys измеряются.
Входные параметры воздействия w не являются последними входными параметрами sys.

Вектор индекса sensors задает который выходные параметры sys измеряются. Эти выходные параметры составляют y. Вектор индекса known задает, какие входные параметры известны (детерминированные). Известные входные параметры составляют u. kalman команда берет остающиеся входные параметры sys быть стохастическими входными параметрами w.

[kalmf,L,P,Mx,Z,My] = kalman(___) также возвращается, инновации получают Mx и My и установившиеся ошибочные ковариации P и Z в течение дискретного времени sys. Можно использовать этот синтаксис с любой из предыдущих комбинаций входных аргументов.

[kalmf,L,P,Mx,Z,My] = kalman(___,type) задает тип средства оценки в течение дискретного времени sys.

type = 'current' — Вычислите выходные оценки $\hat{y} [n | n]$ и оценки состояния $\hat{x} [n | n]$ использование всех доступных измерений до $y [n]$ .
type = 'delayed' — Вычислите выходные оценки $\hat{y} [n | n - 1]$ и оценки состояния $\hat{x} [n | n - 1]$ использование измерений только до $y [n - 1]$ . Задержанное средство оценки легче реализовать внутренние циклы управления.

Можно использовать type входной параметр с любой из предыдущих комбинаций входных аргументов.

Примеры

свернуть все

Спроектируйте фильтр Калмана для объекта SISO

Скрипт Open Live Script

Спроектируйте Фильтр Калмана для объекта, который имеет аддитивный белый шум w на входе и v на выходе, как показано в следующей схеме.

Примите, что объект имеет следующие матрицы пространства состояний и является объектом дискретного времени с незаданным шагом расчета (Ts = -1).

A = [1.1269   -0.4940    0.1129 
     1.0000         0         0 
          0    1.0000         0];

B = [-0.3832
      0.5919
      0.5191];

C = [1 0 0];

D = 0;

Plant = ss(A,B,C,D,-1);
Plant.InputName = 'un';
Plant.OutputName = 'yt';

Использовать kalman, необходимо предоставить модель sys это имеет вход для шумового w. Таким образом, sys различный как Plant, потому что Plant берет вход un = u + w. Можно создать sys путем создания соединения подведения итогов для шумового входа.

Sum = sumblk('un = u + w');
sys = connect(Plant,Sum,{'u','w'},'yt');

Эквивалентно, можно использовать sys = Plant*[1 1].

Задайте шумовые ковариации. Поскольку объект имеет один шумовой вход и один выход, эти значения являются скаляром. На практике эти значения являются свойствами источников шума в вашей системе, которую вы определяете измерением или другим знанием вашей системы. В данном примере примите, что оба источника шума имеют модульную ковариацию и не коррелируются (N = 0).

Q = 1;
R = 1;
N = 0;

Спроектируйте фильтр.

[kalmf,L,P] = kalman(sys,Q,R,N);
size(kalmf)

State-space model with 4 outputs, 2 inputs, and 3 states.

Фильтр Калмана kalmf модель в пространстве состояний, имеющая два входных параметров и четыре выходных параметров. kalmf берет в качестве входных параметров входной сигнал объекта u и шумный объект выход $y = y_{t} + v$ . Первый выход является предполагаемым истинным объектом выход $y_{}^{ˆ}$ . Остающиеся три выходных параметров являются оценками состояния $x_{}^{ˆ}$ . Исследуйте имена ввода и вывода kalmf чтобы видеть, как kalman помечает их соответственно.

kalmf.InputName

ans = 2x1 cell
    {'u' }
    {'yt'}

kalmf.OutputName

ans = 4x1 cell
    {'yt_e'}
    {'x1_e'}
    {'x2_e'}
    {'x3_e'}

Исследуйте усиления Кальмана L. Для объекта SISO с тремя состояниями, L трехэлементный вектор-столбец.

Для примера, который показывает, как использовать kalmf чтобы уменьшать погрешность измерения из-за шума, смотрите Кальмана Филтеринга.

Спроектируйте фильтр Калмана для объекта MIMO

Скрипт Open Live Script

Рассмотрите объект с тремя входными параметрами, одни из которых представляют шум процесса w и два измеренных выходных параметров. Объект имеет четыре состояния.

При принятии следующих матриц пространства состояний создайте sys.

A = [-0.71  0.06 -0.19 -0.17;
      0.06 -0.52 -0.03  0.30;
     -0.19 -0.03 -0.24 -0.02;
     -0.17  0.30 -0.02 -0.41];

B = [ 1.44  2.91   0;
     -1.97  0.83 -0.27;
     -0.20  1.39  1.10;
     -1.2   0    -0.28];

C = [ 0    -0.36 -1.58 0.28;
     -2.05  0     0.51 0.03];

D = zeros(2,3);

sys = ss(A,B,C,D);
sys.InputName = {'u1','u2','w'};
sys.OutputName = {'y1','y2'};

Поскольку объект имеет только один вход шума процесса, ковариация Q является скаляром. В данном примере примите, что шум процесса имеет модульную ковариацию.

Q = 1;

kalman использует размерности Q определить, какие входные параметры известны и которые являются шумовыми входными параметрами. Для скалярного QКалман принимает один шумовой вход и использует последний вход, если вы не задаете в противном случае (см. Объект с Неизмеренными Выходными параметрами).

Для шума измерения на этих двух выходных параметрах задайте шумовую ковариационную матрицу 2 на 2. В данном примере используйте модульное отклонение для первого выхода и отклонение 1,3 для второго выхода. Обнулите недиагональные значения, чтобы указать, что два шумовых канала являются некоррелироваными.

R = [1 0;
     0 1.3];

Спроектируйте Фильтр Калмана.

[kalmf,L,P] = kalman(sys,Q,R);

Исследуйте вводы и выводы. kalman использует InputName, OutputName, InputGroup, и OutputGroup свойства kalmf помочь вам отслеживать какой вводы и выводы kalmf представлять.

kalmf.InputGroup

ans = struct with fields:
     KnownInput: [1 2]
    Measurement: [3 4]

kalmf.InputName

ans = 4x1 cell
    {'u1'}
    {'u2'}
    {'y1'}
    {'y2'}

kalmf.OutputGroup

ans = struct with fields:
    OutputEstimate: [1 2]
     StateEstimate: [3 4 5 6]

kalmf.OutputName

ans = 6x1 cell
    {'y1_e'}
    {'y2_e'}
    {'x1_e'}
    {'x2_e'}
    {'x3_e'}
    {'x4_e'}

Таким образом два известных входных параметров u1 и u2 первые два входных параметров kalmf и два измеренных выходных параметров y1 и y2 последние два входных параметров к kalmf. Для выходных параметров kalmf, первыми двумя являются предполагаемые выходные параметры, и остающиеся четыре являются оценками состояния. Чтобы использовать Фильтр Калмана, соедините эти входные параметры с объектом и шумовыми сигналами способом, аналогичным показанному для объекта SISO в Кальмане Филтеринге.

Объект с неизмеренными Выходными параметрами

Скрипт Open Live Script

Рассмотрите объект с четырьмя входными параметрами и двумя выходными параметрами. Первые и третьи входные параметры известны, в то время как вторые и четвертые входные параметры представляют шум процесса. Объект также имеет два выходных параметров, но только второй из них измеряется.

Используйте следующие матрицы пространства состояний, чтобы создать sys.

A = [-0.37  0.14 -0.01  0.04;
     0.14 -1.89  0.98 -0.11;
    -0.01  0.98 -0.96 -0.14;
     0.04 -0.11 -0.14 -0.95];

B = [-0.07 -2.32  0.68  0.10;
     -2.49  0.08  0     0.83;
      0    -0.95  0     0.54;
     -2.19  0.41  0.45  0.90];

C = [ 0     0    -0.50 -0.38;
     -0.15 -2.12 -1.27  0.65];

D = zeros(2,4);

sys = ss(A,B,C,D,-1);    % Discrete with unspecified sample time

sys.InputName = {'u1','w1','u2','w2'};
sys.OutputName = {'yun','ym'};

Использовать kalman чтобы спроектировать фильтр для этой системы, используйте known и sensors измеряются входные параметры, чтобы задать, какие входные параметры к объекту известны и которые выводят.

known = [1 3];
sensors = [2];

Задайте шумовые ковариации и спроектируйте фильтр.

Q = eye(2);
R = 1;
N = 0;

[kalmf,L,P] = kalman(sys,Q,R,N,sensors,known);

Исследование меток ввода и вывода kalmf показывает входные параметры, что фильтр ожидает и выходные параметры, которые он возвращает.

kalmf.InputGroup

ans = struct with fields:
     KnownInput: [1 2]
    Measurement: 3

kalmf.InputName

ans = 3x1 cell
    {'u1'}
    {'u2'}
    {'ym'}

kalmf берет в качестве входных параметров два известных входных параметров sys и шумные измеренные выходные параметры sys.

kalmf.OutputGroup

ans = struct with fields:
    OutputEstimate: 1
     StateEstimate: [2 3 4 5]

Первый выход kalmf его оценка истинного значения измеренного объекта выход. Остающиеся выходные параметры являются оценками состояния.

Входные параметры

свернуть все

`sys` — Модель объекта управления с шумом процесса
`ss` модель

Модель объекта управления с шумом процесса в виде пространства состояний (ss) модель. Объект знал, вводит u, и белый шум процесса вводит w. Объект выход _yt не включает шум измерения.

Diagram showing that sys includes plant dynamics and process noise inputs, but not the additive noise on the plant output.

Можно записать матрицы пространства состояний такой модели объекта управления как:

$A, [B G], C, [D H]$

kalman принимает Гауссов шумовой v на выходе. Таким образом, в непрерывное время, уравнения пространства состояний это kalman работает с:

$\begin{array}{l} \dot{x} = A x + B u + G w \\ y = C x + D u + H w + v \end{array}$

В дискретное время уравнения пространства состояний:

$\begin{array}{l} x [n + 1] = A x [n] + B u [n] + G w [n] \\ y [n] = C x [n] + D u [n] + H w [n] + v [n] \end{array}$

Если вы не используете known входной параметр, kalman использует размер Q определить который входные параметры sys шумовые входные параметры. В этом случае, kalman обрабатывает последний _Nw = size(Q,1) входные параметры как шумовые входные параметры. Когда шум вводит w не последние входные параметры sys, можно использовать known входной параметр, чтобы задать, какие входные параметры объекта известны. kalman обрабатывает остающиеся входные параметры как стохастические.

Для дополнительных ограничений на свойства матриц объекта смотрите Ограничения.

`Q` — Ковариация шума процесса
скаляр | матрица

Ковариация шума процесса в виде скаляра или _Nw-by-_Nw матрица, где _Nw является количеством шумовых входных параметров к объекту. kalman использует размер Q определить который входные параметры sys шумовые входные параметры, беря последний _Nw = size(Q,1) входные параметры, чтобы быть шумовыми входными параметрами, если вы не задаете в противном случае с known входной параметр.

kalman принимает, что шум процесса w является Гауссовым шумом с ковариацией Q = E (ww^T). Когда объект имеет только один вход шума процесса, Q скаляр, равный отклонению w. Когда объект имеет несколько, некоррелированые шумовые входные параметры, Q диагональная матрица. На практике вы определяете соответствующие значения для Q путем измерения или высказывания образованных предположений о шумовых свойствах системы.

`R` — Ковариация шума измерения
скаляр | матрица

Ковариация шума измерения в виде скаляра или _Ny-by-_Ny матрица, где _Ny является количеством объекта выходные параметры. kalman принимает, что шум измерения v является белым шумом с ковариацией R = E (vv^T). Когда объект имеет только один выходной канал, R скаляр, равный отклонению v. Когда объект имеет несколько выходных каналов с некоррелированым шумом измерения, R диагональная матрица. На практике вы определяете соответствующие значения для R путем измерения или высказывания образованных предположений о шумовых свойствах системы.

Для дополнительных ограничений на ковариацию шума измерения смотрите Ограничения.

`N` — Шумовая перекрестная ковариация
0 (значений по умолчанию) | скаляр | матрица

Шумовая перекрестная ковариация в виде скаляра или _Ny-by-_Nw матрица. kalman принимает, что шум процесса w и шум измерения v удовлетворяет N = E (wv^T). Если эти два источника шума не коррелируются, можно не использовать N, который эквивалентен установке N = 0. На практике вы определяете соответствующие значения для N путем измерения или высказывания образованных предположений о шумовых свойствах системы.

`sensors` — Измеренные выходные параметры `sys`
вектор

Измеренные выходные параметры sysВ виде вектора из индексов, идентифицирующих, который выходные параметры sys измеряются. Например, предположите, что ваша система имеет три выходных параметров, но только два из них измеряются, соответствуя первому и трети выходные параметры sys. В этом случае установите sensors = [1 3].

`known` — Известные входные параметры `sys`
вектор

Известные входные параметры sysВ виде вектора из индексов, идентифицирующих, какие входные параметры известны (детерминированные). Например, предположите, что ваша система имеет три входных параметров, но только первые и вторые входные параметры известны. В этом случае установите known = [1 2]Калман интерпретирует любые остающиеся входные параметры sys быть стохастическим.

`type` — Тип средства оценки дискретного времени
`'current'` (значение по умолчанию) | `'delayed'`

Тип средства оценки дискретного времени, чтобы вычислить в виде любого 'current' или 'delayed'. Этот вход релевантен только в течение дискретного времени sys.

'current' — Вычислите выходные оценки $\hat{y} [n | n]$ и оценки состояния $\hat{x} [n | n]$ использование всех доступных измерений до $y [n]$ .
'delayed' — Вычислите выходные оценки $\hat{y} [n | n - 1]$ и оценки состояния $\hat{x} [n | n - 1]$ использование измерений только до $y [n - 1]$ . Задержанное средство оценки легче реализовать внутренние циклы управления.

Для получения дополнительной информации, о как kalman вычисляет текущие и задержанные оценки, смотрите Оценку Дискретного времени.

Выходные аргументы

свернуть все

`kalmf` — Оценка состояния фильтра Калмана
`ss` модель

Оценка состояния фильтра Калмана или фильтр Калмана, возвращенный как пространство состояний (ss) модель. Получившееся средство оценки имеет входные параметры $[u; y]$ и выходные параметры $[\hat{y}; \hat{x}]$ . Другими словами, kalmf берет в качестве входных параметров вход u объекта и шумный объект выход y, и производит, как выводит предполагаемый бесшумный объект выход $\hat{y}$ и предполагаемые значения состояния $\hat{x}$ .

Diagram showing Kalman filter with inputs u and y and outputs y-hat and x-hat.

kalman автоматически устанавливает InputName, OutputName, InputGroup, и OutputGroup свойства kalmf помочь вам отслеживать, которых вводы и выводы соответствуют который сигналы.

Для состояния и выходных уравнений kalmf, смотрите Оценку Оценки и Дискретного времени Непрерывного времени.

`L` — Отфильтруйте усиления
массив

Отфильтруйте усиления, возвращенные как массив размера _Nx-by-_Ny, где _Nx является количеством состояний на объекте, и _Ny является количеством объекта выходные параметры. В непрерывное время уравнение состояния Фильтра Калмана:

$\dot{\hat{x}} = A \hat{x} + B u + L (y - C \hat{x} - D u) .$

В дискретное время уравнение состояния:

$\hat{x} [n + 1 | n] = A \hat{x} [n | n - 1] + B u [n] + L (y [n] - C \hat{x} [n | n - 1] - D u [n]) .$

Для получения дополнительной информации об этих выражениях и как L вычисляется, смотрите Оценку Оценки и Дискретного времени Непрерывного времени.

`PZ` — Установившиеся ошибочные ковариации
массив

Установившиеся ошибочные ковариации, возвращенные как _Nx-by-_Nx, где _Nx является количеством состояний на объекте. Фильтр Калмана вычисляет оценки состояния, которые минимизируют P. В непрерывное время установившейся ошибочной ковариацией дают:

$P = \lim_{t \to \infty} E ({x - \hat{x}} {x - \hat{x}}^{T}) .$

В дискретное время установившимися ошибочными ковариациями дают:

$\begin{array}{l} P = \lim_{n \to \infty} E ({x [n] - \hat{x} [n | n - 1]} {x [n] - \hat{x} [n | n - 1]}^{T}), \\ Z = \lim_{n \to \infty} E ({x [n] - \hat{x} [n | n]} {x [n] - \hat{x} [n | n]}^{T}) . \end{array}$

Для получения дальнейшей информации об этих количествах и как kalman использует их, смотрите Оценку Оценки и Дискретного времени Непрерывного времени.

`Mx`, `My` — Инновационные усиления средств оценки состояния
массив

Инновационные усиления средств оценки состояния для систем дискретного времени, возвращенных как массив.

Mx и My релевантны только когда type = 'current', который является средством оценки по умолчанию для систем дискретного времени. В течение непрерывного времени sys или type = 'delayed', затем Mx = My = [].

Для 'current' введите средство оценки, Mx и My инновационные усиления в уравнениях обновления:

$\hat{x} [n | n] = \hat{x} [n | n - 1] + M_{x} (y [n] - C \hat{x} [n | n - 1] - D u [n])$

$\hat{y} [n | n] = C \hat{x} [n | n - 1] + D u [n] + M_{y} (y [n] - C \hat{x} [n | n - 1] - D u [n])$

Когда не будет никакого прямого сквозного соединения от шумового входа w до объекта выход y (то есть, когда H = 0, смотрите Оценку Дискретного времени), затем $M_{y} = C M_{x}$ , и выходная оценка упрощает до $\hat{y} [n | n] = C \hat{x} [n | n] + D u [n]$ .

Размерности массивов Mx и My зависьте от размерностей sys можно следующим образом.

Mx — _Nx-by-_Ny, где _Nx является количеством состояний на объекте и _Ny, является количеством выходных параметров.
My — _Ny-by-_Ny.

Для получения дополнительной информации, о как kalman получает Mx и My, смотрите Оценку Дискретного времени.

Ограничения

Объект и шумовые данные должны удовлетворить:

(C, A), обнаруживаемо, где:
$\bar{R} > 0$ и $[\begin{matrix} \bar{Q} & \bar{N}; \begin{matrix} {\bar{N}}^{'} & \bar{R} \end{matrix} \end{matrix}] \geq 0$ , где
$[\begin{matrix} \bar{Q} & \bar{N} \\ {\bar{N}}^{'} & \bar{R} \end{matrix}] = [\begin{matrix} G & 0 \\ H & I \end{matrix}] [\begin{matrix} Q & N \\ N^{'} & R \end{matrix}] {[\begin{matrix} G & 0 \\ H & I \end{matrix}]}^{'} .$
$(A - \bar{N} {\bar{R}}^{- 1} C, \bar{Q} - \bar{N} {\bar{R}}^{- 1} {\bar{N}}^{T})$ не имеет никакого неконтролируемого режима на мнимой оси в непрерывное время, или на модульном круге в дискретное время.

Алгоритмы

свернуть все

Оценка непрерывного времени

Считайте объект непрерывного времени с известными входными параметрами u, белый шум процесса w и белый шум измерения v:

$\begin{array}{l} \dot{x} = A x + B u + G w \\ y = C x + D u + H w + v \end{array}$

Шум сигнализирует, что w и v удовлетворяют:

$E (w) = E (v) = 0, E (w w^{T}) = Q, E (v v^{T}) = R, E (w v^{T}) = N$

Фильтр Калмана или Оценка состояния фильтра Калмана, вычисляет оценку состояния $\hat{x} (t)$ это минимизирует установившуюся ошибочную ковариацию:

$P = \lim_{t \to \infty} E ({x - \hat{x}} {x - \hat{x}}^{T}) .$

Фильтр Калмана имеет следующее состояние и выходные уравнения:

$\begin{array}{l} \frac{d \hat{x}}{d t} = A \hat{x} + B u + L (y - C \hat{x} - D u) \\ [\begin{matrix} \hat{y} \\ \hat{x} \end{matrix}] = [\begin{matrix} C \\ I \end{matrix}] \hat{x} + [\begin{matrix} D \\ 0 \end{matrix}] u \end{array}$

Чтобы получить фильтр получают L, kalman решает алгебраическое уравнение Riccati, чтобы получить

$L = (P C^{T} + \bar{N}) {\bar{R}}^{- 1}$

где

$\begin{array}{l} \bar{R} = R + H N + N^{T} H^{T} + H Q H^{T} \\ \bar{N} = G (Q H^{T} + N) \end{array}$

P решает соответствующее алгебраическое уравнение Riccati.

Средство оценки использует известные входные параметры u и измерения y, чтобы сгенерировать выход и оценки состояния $\hat{y}$ и $\hat{x}$ .

Оценка дискретного времени

Дискретным объектом дают:

$\begin{array}{l} x [n + 1] = A x [n] + B u [n] + G w [n] \\ y [n] = C x [n] + D u [n] + H w [n] + v [n] \end{array}$

В дискретное время шум сигнализирует, что w и v удовлетворяют:

$E (w [n] w {[n]}^{T}) = Q, E (v [n] v {[n]}^{T}) = R, E (w [n] v {[n]}^{T}) = N$

Средство оценки дискретного времени имеет следующее уравнение состояния:

$\hat{x} [n + 1 | n] = A \hat{x} [n | n - 1] + B u [n] + L (y [n] - C \hat{x} [n | n - 1] - D u [n]) .$

kalman решает дискретное уравнение Riccati, чтобы получить матрицу усиления L:

$L = (A P C^{T} + \bar{N}) {(C P C^{T} + \bar{R})}^{- 1}$

где

$\begin{array}{l} \bar{R} = R + H N + N^{T} H^{T} + H Q H^{T} \\ \bar{N} = G (Q H^{T} + N) \end{array}$

kalman может вычислить два варианта Оценки состояния фильтра Калмана дискретного времени, текущее средство оценки (type = 'current') и задержанное средство оценки (type = 'delayed').

Текущее средство оценки — Generates оценки выхода $\hat{y} [n | n]$ и оценки состояния $\hat{x} [n | n]$ использование всех доступных измерений до $y [n]$ . Это средство оценки имеет выходное уравнение

$[\begin{matrix} \hat{y} [n | n] \\ \hat{x} [n | n] \end{matrix}] = [\begin{matrix} (I - M_{y}) C \\ I - M_{x} C \end{matrix}] \hat{x} [n | n - 1] + [\begin{matrix} (I - M_{y}) D & M_{y} \\ - M_{x} D & M_{x} \end{matrix}] [\begin{matrix} u [n] \\ y [n] \end{matrix}] .$
где инновации получают _Mx, и _My заданы как:
$\begin{matrix} M_{x} = P C^{T} {(C P C^{T} + \bar{R})}^{- 1}, \\ M_{y} = (C P C^{T} + H Q H^{T} + H N) {(C P C^{T} + \bar{R})}^{- 1} . \end{matrix}$
Таким образом _Mx обновляет оценку состояния $\hat{x} [n | n - 1]$ использование нового измерения $y [n]$ :
$\hat{x} [n | n] = \hat{x} [n | n - 1] + M_{x} (y [n] - C \hat{x} [n | n - 1] - D u [n])$
Точно так же _My вычисляет обновленную выходную оценку:
$\hat{y} [n | n] = C \hat{x} [n | n - 1] + D u [n] + M_{y} (y [n] - C \hat{x} [n | n - 1] - D u [n])$
Когда H = 0, затем $M_{y} = C M_{x}$ , и выходная оценка упрощает до $\hat{y} [n | n] = C \hat{x} [n | n] + D u [n]$ .
Задержанное средство оценки — Generates оценки выхода $\hat{y} [n | n - 1]$ и оценки состояния $\hat{x} [n | n - 1]$ использование измерений только до _yv [n –1]. Это средство оценки имеет выходное уравнение:

$[\begin{matrix} \hat{y} [n | n - 1] \\ \hat{x} [n | n - 1] \end{matrix}] = [\begin{matrix} C \\ I \end{matrix}] \hat{x} [n | n - 1] + [\begin{matrix} D & 0 \\ 0 & 0 \end{matrix}] [\begin{matrix} u [n] \\ y [n] \end{matrix}]$
Задержанное средство оценки легче развернуть внутренние циклы управления.

Документация

kalman

Синтаксис

Описание

Примеры

Спроектируйте фильтр Калмана для объекта SISO

Спроектируйте фильтр Калмана для объекта MIMO

Объект с неизмеренными Выходными параметрами

Входные параметры

`sys` — Модель объекта управления с шумом процесса
`ss` модель

`Q` — Ковариация шума процесса
скаляр | матрица

`R` — Ковариация шума измерения
скаляр | матрица

`N` — Шумовая перекрестная ковариация
0 (значений по умолчанию) | скаляр | матрица

`sensors` — Измеренные выходные параметры `sys`
вектор

`known` — Известные входные параметры `sys`
вектор

`type` — Тип средства оценки дискретного времени
`'current'` (значение по умолчанию) | `'delayed'`

Выходные аргументы

`kalmf` — Оценка состояния фильтра Калмана
`ss` модель

`L` — Отфильтруйте усиления
массив

`PZ` — Установившиеся ошибочные ковариации
массив

`Mx`, `My` — Инновационные усиления средств оценки состояния
массив

Ограничения

Алгоритмы

Оценка непрерывного времени

Оценка дискретного времени

Смотрите также

Блоки

Темы

Документация Control System Toolbox

Поддержка

Документация

kalman

Синтаксис

Описание

Примеры

Спроектируйте фильтр Калмана для объекта SISO

Спроектируйте фильтр Калмана для объекта MIMO

Объект с неизмеренными Выходными параметрами

Входные параметры

sys — Модель объекта управления с шумом процесса ss модель

Q — Ковариация шума процесса скаляр | матрица

R — Ковариация шума измерения скаляр | матрица

N — Шумовая перекрестная ковариация 0 (значений по умолчанию) | скаляр | матрица

sensors — Измеренные выходные параметры sys вектор

known — Известные входные параметры sys вектор

type — Тип средства оценки дискретного времени 'current' (значение по умолчанию) | 'delayed'

Выходные аргументы

kalmf — Оценка состояния фильтра Калмана ss модель

L — Отфильтруйте усиления массив

PZ — Установившиеся ошибочные ковариации массив

Mx, My — Инновационные усиления средств оценки состояния массив

Ограничения

Алгоритмы

Оценка непрерывного времени

Оценка дискретного времени

Смотрите также

Блоки

Темы

Документация Control System Toolbox

Поддержка

`sys` — Модель объекта управления с шумом процесса
`ss` модель

`Q` — Ковариация шума процесса
скаляр | матрица

`R` — Ковариация шума измерения
скаляр | матрица

`N` — Шумовая перекрестная ковариация
0 (значений по умолчанию) | скаляр | матрица

`sensors` — Измеренные выходные параметры `sys`
вектор

`known` — Известные входные параметры `sys`
вектор

`type` — Тип средства оценки дискретного времени
`'current'` (значение по умолчанию) | `'delayed'`

`kalmf` — Оценка состояния фильтра Калмана
`ss` модель

`L` — Отфильтруйте усиления
массив

`PZ` — Установившиеся ошибочные ковариации
массив

`Mx`, `My` — Инновационные усиления средств оценки состояния
массив