Подбор кривой наименьших квадратов

Введение

Программное обеспечение Curve Fitting Toolbox™ использует метод наименьших квадратов когда подходящие данные. Подбор кривой требует параметрической модели, которая связывает данные об ответе с данными о предикторе с одним или несколькими коэффициентами. Результатом подходящего процесса является оценка коэффициентов модели.

Чтобы получить содействующие оценки, метод наименьших квадратов минимизирует суммированный квадрат остаточных значений. Невязка для i th точка данных _ri задан как различие между наблюдаемым значением отклика _yi и подходящим значением отклика _ŷi, и идентифицирован как ошибка, сопоставленная с данными.

$\begin{array}{l} r_{i} = y_{i} - {\hat{y}}_{i} \\ residual=data - подгонка \end{array}$

Суммированным квадратом остаточных значений дают

$S = \sum_{i = 1}^{n} r_{i}^{2} = \sum_{i = 1}^{n} {(y_{i} - {\hat{y}}_{i})}^{2}$

где n является количеством точек данных, включенных в подгонку, и S является ошибочной оценкой суммы квадратов. Поддерживаемые типы подбора кривой наименьших квадратов включают:

Линейный метод наименьших квадратов
Взвешенный линейный метод наименьших квадратов
Устойчивые наименьшие квадраты
Нелинейный метод наименьших квадратов

Распределения ошибок

Когда подходящие данные, которые содержат случайные изменения, существуют два важных предположения, которые обычно делаются об ошибке:

Ошибка существует только в данных об ответе, а не в данных о предикторе.
Ошибки случайны и следуют за нормальным (Гауссовым) распределением с нулевым средним и постоянным отклонением, σ².

Второе предположение часто описывается как

$e r r o r \sim N (0, σ^{2})$

Ошибки приняты, чтобы быть нормально распределенными, потому что нормальное распределение часто предоставляет соответствующее приближение распределению многих измеренных количеств. Несмотря на то, что наименьшие квадраты, подходящий метод не принимает нормально распределенные ошибки при вычислении оценок параметра, метод, работают лучше всего на данные, которые не содержат большое количество случайных ошибок с экстремумами. Нормальное распределение является одним из вероятностных распределений, в которых экстремальные случайные ошибки являются редкими. Однако статистические результаты, такие как доверие и границы предсказания действительно требуют нормально распределенных ошибок для своей валидности.

Если среднее значение ошибок является нулем, то ошибки чисто случайны. Если среднее значение не является нулем, то может случиться так, что модель не является правильным выбором для ваших данных, или ошибки не чисто случайны и содержат систематические ошибки.

Постоянное отклонение в данных подразумевает, что “распространение” ошибок является постоянным. Данные, которые имеют то же отклонение, как иногда говорят, equal quality.

Предположение, что случайные ошибки имеют постоянное отклонение, не неявно к регрессии метода взвешенных наименьших квадратов. Вместо этого это принято, что веса, обеспеченные в подходящей процедуре правильно, указывают на отличающиеся уровни качества, существующего в данных. Веса затем используются, чтобы настроить сумму влияния, которое каждая точка данных имеет на оценки подходящих коэффициентов к соответствующему уровню.

Линейный метод наименьших квадратов

Программное обеспечение Curve Fitting Toolbox использует метод линейного метода наименьших квадратов, чтобы подбирать линейную модель к данным. Линейная модель задана как уравнение, которое линейно в коэффициентах. Например, полиномы линейны, но Gaussians не. Чтобы проиллюстрировать линейный метод наименьших квадратов подходящий процесс, предположите, что у вас есть точки данных n, которые могут быть смоделированы полиномом первой степени.

$y = p_{1} x + p_{2}$

Чтобы решить это уравнение для неизвестных коэффициентов p ₁ и p ₂, вы пишете S как систему n одновременные линейные уравнения в двух неизвестных. Если n больше количества неизвестных, то система уравнений сверхопределяется.

$S = \sum_{i = 1}^{n} {(y_{i} - (p_{1} x_{i} + p_{2}))}^{2}$

Поскольку наименьшие квадраты, подходящий процесс минимизирует суммированный квадрат остаточных значений, коэффициенты, определяются путем дифференциации S относительно каждого параметра и установки равного нулю результата.

$\begin{array}{l} \frac{\partial S}{\partial p_{1}} = - 2 \sum_{i = 1}^{n} x_{i} (y_{i} - (p_{1} x_{i} + p_{2})) = 0 \\ \frac{\partial S}{\partial p_{2}} = - 2 \sum_{i = 1}^{n} (y_{i} - (p_{1} x_{i} + p_{2})) = 0 \end{array}$

Оценки истинных параметров обычно представляются b. Заменяя b ₁ и b ₂ для p ₁ и p ₂, предыдущие уравнения становятся

$\begin{matrix} \sum x_{i} (y_{i} - (b_{1} x_{i} + b_{2})) = 0 \\ \sum (y_{i} - (b_{1} x_{i} + b_{2})) = 0 \end{matrix}$

где суммирование, запущенное от i = 1 к n. Нормальные уравнения определены как

$\begin{matrix} b_{1} \sum x_{i}^{2} + b_{2} \sum x_{i} = \sum x_{i} y_{i} \\ b_{1} \sum x_{i} + n b_{2} = \sum y_{i} \end{matrix}$

Решение для b ₁

$b_{1} = \frac{n \sum x_{i} y_{i} - \sum x_{i} \sum y_{i}}{n \sum x_{i}^{2} - {(\sum x_{i})}^{2}}$

Решение для b ₂ использования b ₁ значение

$b_{2} = \frac{1}{n} (\sum y_{i} - b_{1} \sum x_{i})$

Как вы видите, оценивая коэффициенты, p ₁ и p ₂ требует только нескольких простых вычислений. Расширение этого примера к более высокому полиному степени является прямым несмотря на то, что немного утомительный. Все, что требуется, является дополнительным нормальным уравнением для каждого линейного члена, добавленного к модели.

В матричной форме линейные модели даны формулой

y = X β + ε

где

y является n-by-1 вектор из ответов.
β m-by-1 вектор из коэффициентов.
X является n-by-m матрица проекта для модели.
ε n-by-1 вектор из ошибок.

Для полинома первой степени уравнения n в двух неизвестных описываются в терминах y, X и β как

$[\begin{matrix} y_{1} \\ y_{2} \\ y_{3} \\ . \\ . \\ . \\ y_{n} \end{matrix}] = [\begin{matrix} x_{1} 1 \\ x_{2} 1 \\ x_{3} 1 \\ . \\ . \\ . \\ x_{n} 1 \end{matrix}] \times [\begin{array}{l} p_{1} \\ p_{2} \end{array}]$

Решением методом наименьших квадратов к проблеме является векторный b, который оценивает неизвестный вектор из коэффициентов β. Нормальными уравнениями дают

X^TX) b = X^Ty

где X^T транспонирование матрицы проекта X. Решение для b,

b = (X^TX^–1 X^Ty

Используйте MATLAB^® оператор обратной косой черты (mldivide) решить систему одновременных линейных уравнений для неизвестных коэффициентов. Поскольку инвертирование X^TX может привести к недопустимым погрешностям округления, оператор обратной косой черты использует разложение QR с поворотом, который является очень устойчивым алгоритмом численно. Обратитесь к Арифметическим операциям для получения дополнительной информации об операторе обратной косой черты и разложении QR.

Можно включить b назад в формулу модели, чтобы получить предсказанные значения отклика, ŷ.

ŷ = Xb = Hy

H = X (X^TX^–1 X^T

Шляпа (циркумфлекс) по букве обозначает оценку параметра или предсказания из модели. Матричный H проекции называется матрицей шляпы, потому что это помещает шляпу на y.

Остаточными значениями дают

r = y – ŷ = (1–H) y

Метод взвешенных наименьших квадратов

Это обычно принимается, что данные об ответе имеют равное качество и, поэтому, имеют постоянное отклонение. Если это предположение нарушено, ваша подходящая сила незаконно под влиянием данных низкого качества. Чтобы улучшить подгонку, можно использовать регрессию метода взвешенных наименьших квадратов, где дополнительный масштабный коэффициент (вес) включен в подходящий процесс. Регрессия метода взвешенных наименьших квадратов минимизирует ошибочную оценку

$s = \sum_{i = 1}^{n} w_{i} {(y_{i} - {\hat{y}}_{i})}^{2}$

где _wi является весами. Веса определяют, насколько каждое значение отклика влияет на итоговые оценки параметра. Высококачественная точка данных влияет на подгонку больше, чем низкокачественная точка данных. Взвешивание ваших данных рекомендуется, если веса известны, или если существует выравнивание, что они следуют за конкретной формой.

Веса изменяют выражение для оценок параметра b следующим образом,

$b = \hat{β} = {(X^{T} W X)}^{- 1} X^{T} W y$

где W дан диагональными элементами матрицы веса w.

Можно часто определять, не являются ли отклонения постоянными подгонкой данных и графическим выводом остаточных значений. В графике, показанном ниже, данные содержат, реплицируют данные различного качества, и подгонка принята, чтобы быть правильной. Данные о низком качестве показаны в графике остаточных значений, который имеет форму “трубы”, где маленькие значения предиктора дают к большему рассеянию в значениях отклика, чем большие значения предиктора.

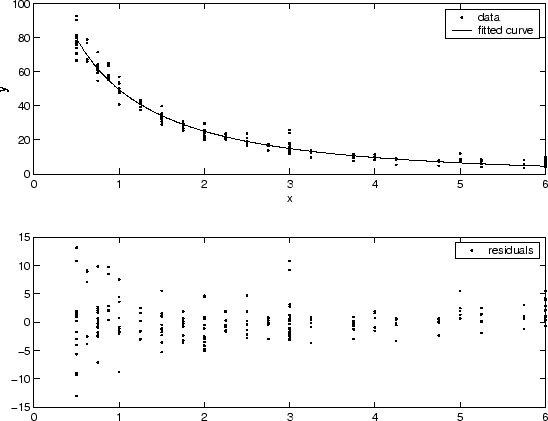
Веса, которые вы предоставляете, должны преобразовать отклонения ответа к постоянному значению. Если вы знаете отклонения погрешностей измерения в ваших данных, то весами дают

$w_{i} = 1 / σ_{i}^{2}$

Или, если у вас только есть оценки ошибочной переменной для каждой точки данных, она обычно достаточна, чтобы использовать те оценки вместо истинного отклонения. Если вы не знаете отклонений, это достаточно, чтобы задать веса на относительном масштабе. Обратите внимание на то, что полный термин отклонения оценивается, даже когда веса были заданы. В этом экземпляре веса задают относительный вес к каждой точке в подгонке, но не взяты, чтобы задать точное отклонение каждой точки.

Например, если каждая точка данных является средним значением нескольких независимых измерений, это может быть целесообразно использовать те количества измерений как веса.

Устойчивые наименьшие квадраты

Это обычно принимается, что ошибки ответа следуют за нормальным распределением, и что экстремумы редки. Однако, названные выбросы экстремумов действительно происходят.

Основной недостаток подбора кривой наименьших квадратов является своей чувствительностью к выбросам. Выбросы имеют большое влияние на подгонку, потому что обработка на квадрат остаточным значениям увеличивает эффекты этих экстремальных точек данных. Чтобы минимизировать влияние выбросов, можно соответствовать данным с помощью устойчивой регрессии наименьших квадратов. Тулбокс предоставляет эти два устойчивых метода регрессии:

Наименее абсолютные остаточные значения (LAR) — метод LAR находит кривую, которая минимизирует абсолютную разность остаточных значений, а не различия в квадрате. Поэтому экстремумы имеют меньшее влияние на подгонку.
Веса Bisquare — Этот метод минимизирует взвешенную сумму квадратов, где вес, данный каждой точке данных, зависит от того, как далеко точка от подходящей линии. Точки около линии получают полный вес. Точки дальше от линии получают уменьшаемый вес. Точки, которые более далеки от линии, чем, ожидались бы случайным шансом, получают нулевой вес.
Для большинства случаев bisquare метод веса предпочтен по LAR, потому что это одновременно стремится найти кривую, которая соответствует объему данных с помощью обычного подхода наименьших квадратов, и это минимизирует эффект выбросов.

Устойчивый подбор кривой bisquare весами использует итеративно перевзвешенный алгоритм наименьших квадратов и выполняет эту процедуру:

Подбирайте модель методом взвешенных наименьших квадратов.
Вычислите настроенные остаточные значения и стандартизируйте их. Настроенными остаточными значениями дают
$r_{a d j} = \frac{r_{i}}{\sqrt{1 - h_{i}}}$
_ri является обычными остаточными значениями наименьших квадратов, и _hi рычаги, которые настраивают остаточные значения путем сокращения веса точек данных высоких рычагов, которые оказывают большое влияние на метод наименьших квадратов. Стандартизированными настроенными остаточными значениями дают
$u = \frac{r_{a d j}}{K s}$
K является настройкой, постоянной равный 4,685, и s является устойчивым стандартным отклонением, данным MAD/0.6745, где MAD является средним абсолютным отклонением остаточных значений.
Вычислите устойчивые веса в зависимости от u. bisquare весами дают
$w_{i} = {\begin{matrix} {(1 - {(u_{i})}^{2})}^{2} & | u_{i} | < 1 \\ 0 & | u_{i} | \geq 1 \end{matrix}$
Обратите внимание на то, что, если вы предоставляете свой собственный вектор веса регрессии, итоговый вес является продуктом устойчивого веса и веса регрессии.
Если подгонка сходится, то вы сделаны. В противном случае выполните следующую итерацию подходящей процедуры путем возврата к первому шагу.

График, показанный ниже, сравнивает регулярную линейную подгонку с устойчивой подгонкой с помощью bisquare веса. Заметьте, что устойчивая подгонка следует за объемом данных и не строго под влиянием выбросов.

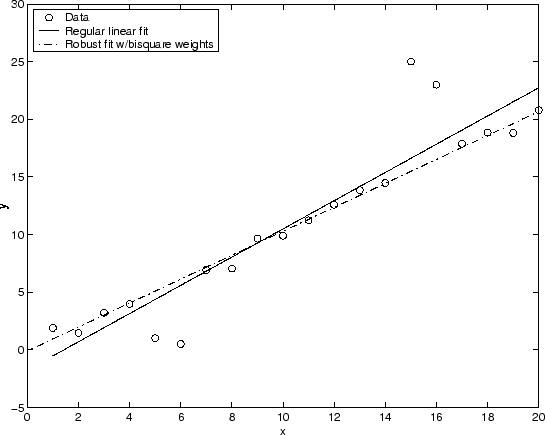
Вместо того, чтобы минимизировать эффекты выбросов при помощи устойчивой регрессии, можно отметить точки данных, которые будут исключены из подгонки. Относитесь, чтобы Удалить Выбросы для получения дополнительной информации.

Нелинейный метод наименьших квадратов

Программное обеспечение Curve Fitting Toolbox использует формулировку нелинейного метода наименьших квадратов, чтобы подбирать нелинейную модель к данным. Нелинейная модель задана как уравнение, которое нелинейно в коэффициентах или комбинации линейных и нелинейных в коэффициентах. Например, Gaussians, отношения полиномов и функции степени все нелинейны.

В матричной форме нелинейные модели даны формулой

y = f (X, β) + ε

где

y является n-by-1 вектор из ответов.
f является функцией β и X.
β m-by-1 вектор из коэффициентов.
X является n-by-m матрица проекта для модели.
ε n-by-1 вектор из ошибок.

Нелинейные модели больше затрудняют, чтобы соответствовать, чем линейные модели, потому что коэффициенты не могут быть оценены с помощью простых матричных методов. Вместо этого итерационный подход требуется, который выполняет эти шаги:

Начните с первоначальной оценки для каждого коэффициента. Для некоторых нелинейных моделей эвристический подход - то, при условии, что производит разумные начальные значения. Для других моделей введены случайные значения на интервале [0,1].
Произведите кривую по экспериментальным точкам для текущего набора коэффициентов. Подходящим значением отклика ŷ дают
ŷ = f (X, b)
и включает вычисление якобиана f (X,b), который задан как матрица частных производных, взятых относительно коэффициентов.
Настройте коэффициенты и определите, улучшается ли подгонка. Направление и величина корректировки зависят от алгоритма подбора. Тулбокс предоставляет эти алгоритмы:
- Доверительная область — Это - алгоритм по умолчанию и должно использоваться, если вы задаете содействующие ограничения. Это может решить трудные нелинейные задачи более эффективно, чем другие алгоритмы, и это представляет улучшение по сравнению с популярным алгоритмом Levenberg-Marquardt.
- Levenberg-Marquardt — Этот алгоритм много лет использовался и, оказалось, работал наиболее часто на широкий спектр нелинейных моделей и начальных значений. Если алгоритм доверительной области не производит разумную подгонку, и у вас нет содействующих ограничений, необходимо попробовать алгоритм Levenberg-Marquardt.
Выполните итерации процесса путем возврата к шагу 2, пока подгонка не достигнет заданных критериев сходимости.

Можно использовать веса и устойчивое соответствование нелинейным моделям, и подходящий процесс изменяется соответственно.

Из-за природы процесса приближения никакой алгоритм не является надежным для всех нелинейных моделей, наборов данных и начальных точек. Поэтому, если вы не достигаете разумной подгонки с помощью начальных точек по умолчанию, алгоритма и критериев сходимости, необходимо экспериментировать с различными вариантами. Обратитесь к Определению Подходящих Опций и Оптимизированных Начальных точек для описания того, как изменить опции по умолчанию. Поскольку нелинейные модели могут быть особенно чувствительны к начальным точкам, это должно быть первой подходящей опцией, которую вы изменяете.

Устойчивый подбор кривой

Скрипт Open Live Script

В этом примере показано, как сравнить эффекты исключения выбросов и устойчивого подбора кривой. Пример показывает, как исключить выбросы на произвольном расстоянии, больше, чем 1,5 стандартных отклонения от модели. Шаги затем сравнивают выбросы удаления с определением устойчивой подгонки, которая дает более низкий вес выбросам.

Создайте базовый синусоидальный сигнал:

xdata = (0:0.1:2*pi)'; 
y0 = sin(xdata);

Добавьте шум в сигнал с непостоянным отклонением.

% Response-dependent Gaussian noise
gnoise = y0.*randn(size(y0));

% Salt-and-pepper noise
spnoise = zeros(size(y0)); 
p = randperm(length(y0));
sppoints = p(1:round(length(p)/5));
spnoise(sppoints) = 5*sign(y0(sppoints));

ydata = y0 + gnoise + spnoise;

Соответствуйте зашумленным данным базовой синусоидальной моделью и задайте 3 выходных аргумента, чтобы получить подходящую информацию включая остаточные значения.

f = fittype('a*sin(b*x)'); 
[fit1,gof,fitinfo] = fit(xdata,ydata,f,'StartPoint',[1 1]);

Исследуйте информацию в fitinfo структуре.

fitinfo

fitinfo = struct with fields:
           numobs: 63
         numparam: 2
        residuals: [63x1 double]
         Jacobian: [63x2 double]
         exitflag: 3
    firstorderopt: 0.0883
       iterations: 5
        funcCount: 18
     cgiterations: 0
        algorithm: 'trust-region-reflective'
         stepsize: 4.1539e-04
          message: 'Success, but fitting stopped because change in residuals less than tolerance (TolFun).'

Получите остаточные значения fitinfo структуры.

residuals = fitinfo.residuals;

Идентифицируйте "выбросы" как точки на произвольном расстоянии, больше, чем 1,5 стандартных отклонения от базовой модели, и переоборудуйте данные исключенными выбросами.

I = abs( residuals) > 1.5 * std( residuals );
outliers = excludedata(xdata,ydata,'indices',I);

fit2 = fit(xdata,ydata,f,'StartPoint',[1 1],...
           'Exclude',outliers);

Сравните эффект исключения выбросов с эффектом предоставления их понижают bisquare вес в устойчивой подгонке.

fit3 = fit(xdata,ydata,f,'StartPoint',[1 1],'Robust','on');

Отобразите на графике данные, выбросы и результаты подгонок. Задайте информативную легенду.

plot(fit1,'r-',xdata,ydata,'k.',outliers,'m*') 
hold on
plot(fit2,'c--')
plot(fit3,'b:')
xlim([0 2*pi])
legend( 'Data', 'Data excluded from second fit', 'Original fit',...
    'Fit with points excluded', 'Robust fit' )
hold off

Figure contains an axes object. The axes object contains 5 objects of type line. These objects represent Data, Data excluded from second fit, Original fit, Fit with points excluded, Robust fit.

Постройте остаточные значения для двух подгонок, рассмотрев выбросы:

figure 
plot(fit2,xdata,ydata,'co','residuals') 
hold on
plot(fit3,xdata,ydata,'bx','residuals')
hold off

Figure contains an axes object. The axes object contains 4 objects of type line. These objects represent data, zero line.

Документация