Экспериментируйте с некоторыми методами приближения сплайна
splinetool открывает Инструмент Сплайна, который позволяет вам экспериментировать с различными методами приближения сплайна. Это предоставляет вам выбор для данных, включая опцию импортирования некоторых данных из рабочей области.
Инструмент сплайна показывают в следующем рисунке выдерживающую сравнение интерполяцию кубическим сплайном со сплайном сглаживания на выборочных данных, созданных путем добавления шума в косинусную функцию.
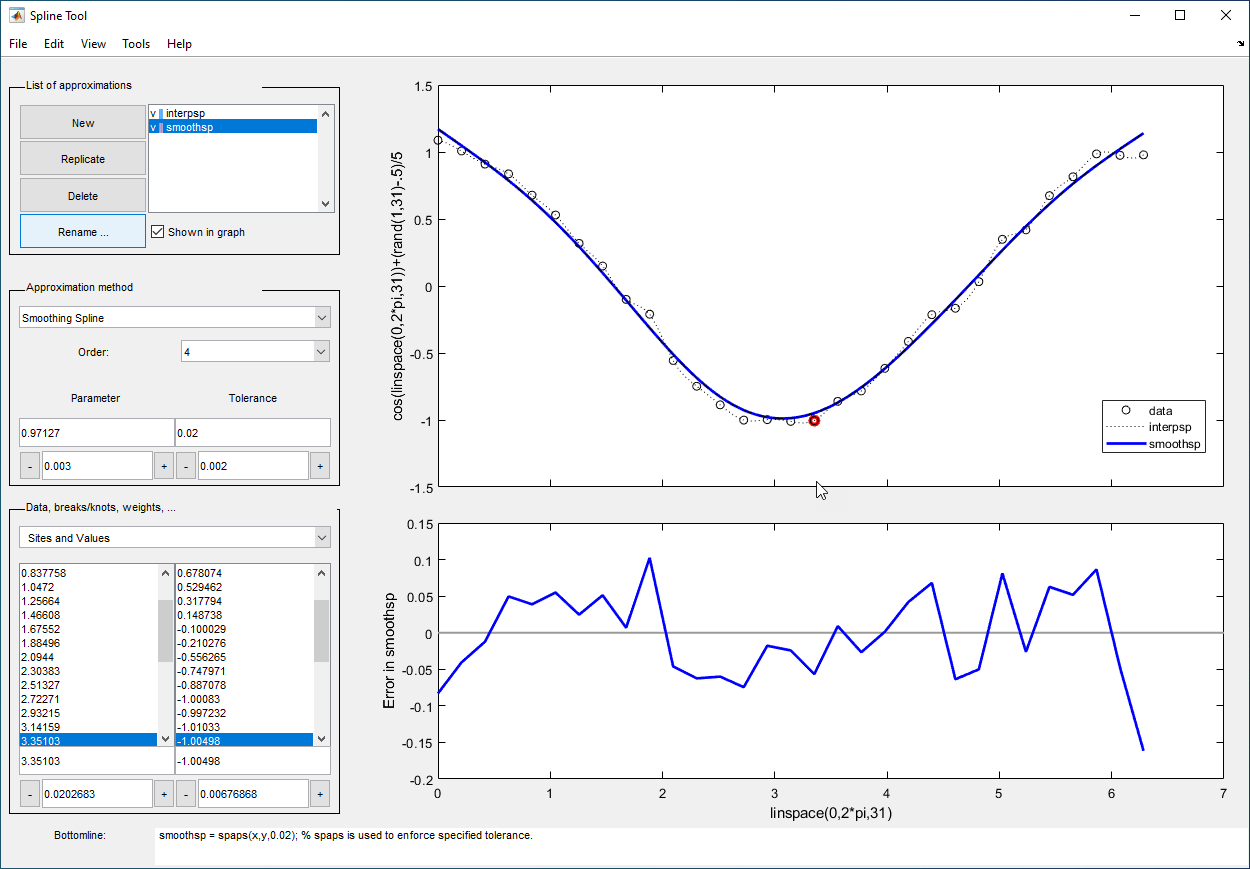
Select Approximation Methods
Методы приближения и опции, поддержанные инструментом, показывают ниже.
Метод приближения | Опция |
|---|---|
Кубический сплайн интерполяции | Настройте тип и значения граничных условий. |
Сглаживание сплайна | Выберите между кубическим (порядок 4) и quintic (порядок 6) сплайны. Настройте значение параметра сглаживания и/или допуска. Настройте веса в мерах по шероховатости и ошибке. |
Приближение наименьших квадратов | Варьируйтесь порядок от 1 до 14. Порядок по умолчанию равняется 4, который дает кубические сплайны аппроксимации. Измените количество полиномиальных частей. Добавьте и переместите узлы, чтобы улучшить подгонку. Настройте веса в ошибочной мере. |
Интерполяция сплайна | Варьируйтесь порядок от 2 до 14. Порядок по умолчанию равняется 4, который дает кубический сплайн interpolants. Если предоставленные узлы по умолчанию не являются удовлетворительными, можно переместить их, чтобы варьироваться подгонка. |
Plot Graphs
Можно сгенерировать и сравнить несколько приближений с теми же данными. Одно из приближений всегда отмечается как “текущее” использование более толстой ширины линии. Следующие отображения доступны:
График данных. Это показывает:
Данные
Приближения, выбранные для отображения в Списке приближений
Текущая последовательность узла или текущая последовательность пропуска
Вспомогательный график (если просматривается) для текущего приближения. Можно просмотреть этот график путем выбора любого из элементов в меню View. Это показывает одно из следующего:
Первая производная
Вторая производная
Ошибка
По умолчанию ошибка является различием между значениями определенных данных и значением приближения на сайтах данных. В частности, ошибка является нулем (до округления), когда приближение является interpolant. Однако, если вы обеспечиваете значения данных путем определения функции, затем отображенная ошибка является различием между этой функцией и текущим приближением. Это также происходит, если вы изменяете y-метку графика данных к имени функции.
Try Menu Options
Можно аннотировать и распечатать графики с Файлом> Печать к меню Figure.
Можно экспортировать данные и приближения к рабочей области для дальнейшего использования или анализа с меню File> Export Data и File> Export Spline, соответственно.
Можно создать с меню File> Generate Code, файл функции, который можно использовать, чтобы сгенерировать, из исходных данных, любые графики, в настоящее время показанные. Этот файл также предоставляет, вы с записанной записью команд раньше генерировали текущие графики.
Можно сохранить с кнопкой Replicate, текущее приближение, прежде чем вы будете экспериментировать далее. Если в более позднее время вы кликаете по сохраненному приближению, инструмент восстанавливает все к способу, которым это было, включая данные, используемые в конструкции сохраненного приближения. Сохраненное приближение сохраняется, даже если вы отредактировали данные при работе над другими приближениями.
Можно добавить, удалить или переместить данные, узлы и пропуски путем щелчка правой кнопкой по графику, или путем выбора соответствующего элемента в меню Edit.
Можно переключить сетку или легенду в графике с меню Tools.