Это очень затрудняет, чтобы знать, какой алгоритм настройки будет самым быстрым для данной проблемы. Это зависит от многих факторов, включая сложность проблемы, количество точек данных в наборе обучающих данных, количество весов и смещений в сети, ошибочной цели, и используется ли сеть для распознавания образов (дискриминантный анализ) или приближение функций (регрессия). Этот раздел сравнивает различные алгоритмы настройки. Сети прямого распространения обучены на шести различных проблемах. Три из проблемного падения категории распознавания образов и этих трех других падают в категории приближения функций. Двумя из проблем являются простые “игрушечные” проблемы, в то время как другие четыре являются проблемами “реального мира”. Сети со множеством различных архитектур и сложностей используются, и сети обучены ко множеству различных уровней точности.
В следующей таблице перечислены алгоритмы, которые тестируются, и акронимы раньше идентифицировали их.
Акроним | Алгоритм | Описание |
|---|---|---|
LM | trainlm | Levenberg-Marquardt |
BFG | trainbfg | Квазиньютон BFGS |
RP | trainrp | Устойчивая обратная связь |
SCG | trainscg | Масштабированный метод сопряженных градиентов |
CGB | traincgb | Метод сопряженных градиентов с Перезапусками Powell/Beale |
CGF | traincgf | Метод сопряженных градиентов Флетчера-Пауэлла |
CGP | traincgp | Метод сопряженных градиентов Полака-Рибиера |
OSS | trainoss | Один секанс шага |
GDX | traingdx | Переменная обратная связь скорости обучения |
В следующей таблице перечислены эти шесть эталонных тестовых задач и некоторые характеристики сетей, учебных процессов и используемых компьютеров.
Проблемный заголовок | Проблемный тип | Структура сети | Ошибочная цель | Компьютер |
|---|---|---|---|---|
SIN | Функциональная аппроксимация | 1-5-1 | 0.002 | Sparc 2 Sun |
Четность | Распознавание образов | 3-10-10-1 | 0.001 | Sparc 2 Sun |
Механизм | Функциональная аппроксимация | 2-30-2 | 0.005 | Предприятие Sun 4000 |
РАК | Распознавание образов | 9-5-5-2 | 0.012 | Sparc 2 Sun |
ХОЛЕСТЕРИН | Функциональная аппроксимация | 21-15-3 | 0.027 | Sparc 20 Sun |
ДИАБЕТ | Распознавание образов | 8-15-15-2 | 0.05 | Sparc 20 Sun |
Первый набор исходных данных является простой проблемой приближения функций. 1-5-1 сеть, с tansig передаточные функции в скрытом слое и линейная передаточная функция в выходном слое, используется, чтобы аппроксимировать один период синусоиды. Следующая таблица обобщает результаты обучения сеть с помощью девяти различных алгоритмов настройки. Каждая запись в таблице представляет 30 различных испытаний, где различные случайные начальные веса используются в каждом испытании. В каждом случае обучена сеть, пока квадратичная невязка не меньше 0.002. Самый быстрый алгоритм для этой проблемы является алгоритмом Levenberg-Marquardt. В среднем это более чем в четыре раза быстрее, чем следующий самый быстрый алгоритм. Это - тип проблемы, для которой алгоритм LM подходит лучше всего — проблема приближения функций, где сеть имеет меньше чем сто весов, и приближение должно быть очень точным.
Алгоритм | Среднее время (время) | Отношение | Min. \times | Максимум время (времена) | Станд. (s) |
|---|---|---|---|---|---|
LM | 1.14 | 1.00 | 0.65 | 1.83 | 0.38 |
BFG | 5.22 | 4.58 | 3.17 | 14.38 | 2.08 |
RP | 5.67 | 4.97 | 2.66 | 17.24 | 3.72 |
SCG | 6.09 | 5.34 | 3.18 | 23.64 | 3.81 |
CGB | 6.61 | 5.80 | 2.99 | 23.65 | 3.67 |
CGF | 7.86 | 6.89 | 3.57 | 31.23 | 4.76 |
CGP | 8.24 | 7.23 | 4.07 | 32.32 | 5.03 |
OSS | 9.64 | 8.46 | 3.97 | 59.63 | 9.79 |
GDX | 27.69 | 24.29 | 17.21 | 258.15 | 43.65 |
Эффективность различных алгоритмов может быть затронута точностью, требуемой приближения. Это показывают в следующем рисунке, который строит среднеквадратичную погрешность по сравнению со временем выполнения (усредненный по 30 испытаниям) для нескольких представительных алгоритмов. Здесь вы видите, что ошибка в алгоритме LM уменьшается намного более быстро со временем, чем другие показанные алгоритмы.
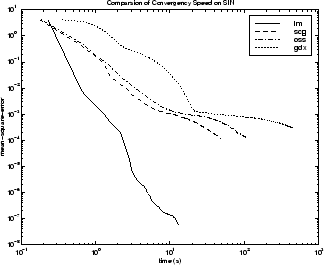
Отношение между алгоритмами далее проиллюстрировано в следующем рисунке, который строит время, требуемое сходиться по сравнению с целью сходимости среднеквадратичной погрешности. Здесь вы видите, что, когда ошибочная цель уменьшается, улучшение, обеспеченное алгоритмом LM, становится более явным. Некоторые алгоритмы выполняют лучше, когда ошибочная цель уменьшается (LM и BFG), и другие алгоритмы ухудшаются, когда ошибочная цель уменьшается (OSS и GDX).
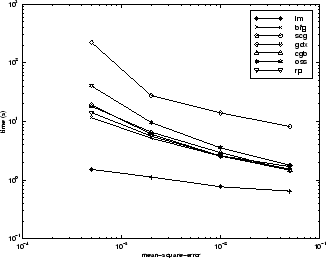
Вторая эталонная тестовая задача является простой проблемой распознавания образов — обнаруживают четность 3-битного номера. Если количество единиц во входном наборе является нечетным, то сеть должна вывести 1; в противном случае это должно вывести-1. Сеть, используемая для этой проблемы, является 3-10-10-1 сетью с tansig нейронами в каждом слое. Следующая таблица обобщает результаты обучения этой сети с девятью различными алгоритмами. Каждая запись в таблице представляет 30 различных испытаний, где различные случайные начальные веса используются в каждом испытании. В каждом случае обучена сеть, пока квадратичная невязка не меньше 0.001. Самый быстрый алгоритм для этой проблемы является эластичным алгоритмом обратного распространения, несмотря на то, что алгоритмы метода сопряженных градиентов (в частности, масштабированный алгоритм метода сопряженных градиентов) почти как быстро. Заметьте, что алгоритм LM не выполняет хорошо на этой проблеме. В общем случае алгоритм LM не выполняет также на проблемах распознавания образов, как он делает на проблемах приближения функций. Алгоритм LM спроектирован для проблем наименьших квадратов, которые приблизительно линейны. Поскольку выходные нейроны в проблемах распознавания образов обычно насыщаются, вы не будете действовать в линейной области.
Алгоритм | Среднее время (время) | Отношение | Min. \times | Максимум время (времена) | Станд. (s) |
|---|---|---|---|---|---|
RP | 3.73 | 1.00 | 2.35 | 6.89 | 1.26 |
SCG | 4.09 | 1.10 | 2.36 | 7.48 | 1.56 |
CGP | 5.13 | 1.38 | 3.50 | 8.73 | 1.05 |
CGB | 5.30 | 1.42 | 3.91 | 11.59 | 1.35 |
CGF | 6.62 | 1.77 | 3.96 | 28.05 | 4.32 |
OSS | 8.00 | 2.14 | 5.06 | 14.41 | 1.92 |
LM | 13.07 | 3.50 | 6.48 | 23.78 | 4.96 |
BFG | 19.68 | 5.28 | 14.19 | 26.64 | 2.85 |
GDX | 27.07 | 7.26 | 25.21 | 28.52 | 0.86 |
Как с проблемами приближения функций, эффективность различных алгоритмов может быть затронута точностью, требуемой сети. Это показывают в следующем рисунке, который строит среднеквадратичную погрешность по сравнению со временем выполнения для некоторых типичных алгоритмов. Алгоритм LM сходится быстро после некоторой точки, но только после того, как другие алгоритмы уже сходились.
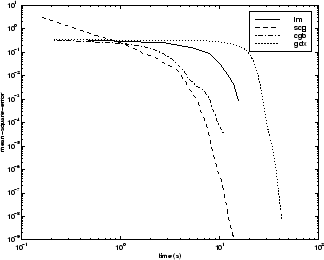
Отношение между алгоритмами далее проиллюстрировано в следующем рисунке, который строит время, требуемое сходиться по сравнению с целью сходимости среднеквадратичной погрешности. Снова вы видите, что некоторые алгоритмы ухудшаются, когда ошибочная цель уменьшается (OSS и BFG).
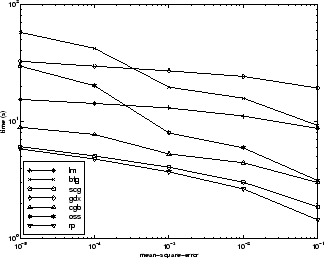
Третья эталонная тестовая задача является реалистическим приближением функций (или нелинейная регрессия) проблема. Данные получены из работы механизма. Входные параметры к сети являются скоростью вращения двигателя и уровнями заправки, и сетевые выходные параметры являются крутящим моментом и уровнями выбросов. Сеть, используемая для этой проблемы, является 2-30-2 сетями с tansig нейронами в скрытом слое и линейными нейронами в выходном слое. Следующая таблица обобщает результаты обучения этой сети с девятью различными алгоритмами. Каждая запись в таблице представляет 30 различных испытаний (10 испытаний за RP и GDX из-за ограничений времени), где различные случайные начальные веса используются в каждом испытании. В каждом случае обучена сеть, пока квадратичная невязка не меньше 0.005. Самый быстрый алгоритм для этой проблемы является алгоритмом LM, сопровождаемым алгоритмом квазиньютона BFGS и алгоритмами метода сопряженных градиентов. Несмотря на то, что это - проблема приближения функций, алгоритм LM не как ясно выше, как это было на наборе данных SIN. В этом случае количество весов и смещений в сети намного больше, чем та, используемая на проблеме SIN (152 по сравнению с 16), и преимущества уменьшения алгоритма LM как количество сетевых увеличений параметров.
Алгоритм | Среднее время (время) | Отношение | Min. \times | Максимум время (времена) | Станд. (s) |
|---|---|---|---|---|---|
LM | 18.45 | 1.00 | 12.01 | 30.03 | 4.27 |
BFG | 27.12 | 1.47 | 16.42 | 47.36 | 5.95 |
SCG | 36.02 | 1.95 | 19.39 | 52.45 | 7.78 |
CGF | 37.93 | 2.06 | 18.89 | 50.34 | 6.12 |
CGB | 39.93 | 2.16 | 23.33 | 55.42 | 7.50 |
CGP | 44.30 | 2.40 | 24.99 | 71.55 | 9.89 |
OSS | 48.71 | 2.64 | 23.51 | 80.90 | 12.33 |
RP | 65.91 | 3.57 | 31.83 | 134.31 | 34.24 |
GDX | 188.50 | 10.22 | 81.59 | 279.90 | 66.67 |
Следующая фигура строит среднеквадратичную погрешность по сравнению со временем выполнения для некоторых типичных алгоритмов. Эффективность алгоритма LM улучшается в зависимости от времени относительно других алгоритмов.
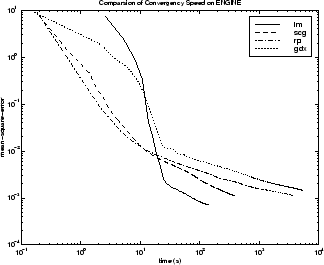
Отношение между алгоритмами далее проиллюстрировано в следующем рисунке, который строит время, требуемое сходиться по сравнению с целью сходимости среднеквадратичной погрешности. Снова вы видите, что некоторые алгоритмы ухудшаются, когда ошибочная цель уменьшается (GDX и RP), в то время как алгоритм LM улучшается.

Четвертая эталонная тестовая задача является реалистическим распознаванием образов (или нелинейный дискриминантный анализ) проблема. Цель сети состоит в том, чтобы классифицировать опухоль или как мягкую или как злостную на основе описаний ячейки, собранных микроскопическим исследованием. Входные атрибуты включают толщину глыбы, однородность размера ячейки и формы ячейки, суммы крайней адгезии и частоты пустых ядер. Данные были получены из Больниц Висконсинского университета, Мадисон, от доктора Вильгельма Х. Вольберга. Сеть, используемая для этой проблемы, является 9-5-5-2 сетями с tansig нейронами во всех слоях. Следующая таблица обобщает результаты обучения этой сети с девятью различными алгоритмами. Каждая запись в таблице представляет 30 различных испытаний, где различные случайные начальные веса используются в каждом испытании. В каждом случае обучена сеть, пока квадратичная невязка не меньше 0.012. Нескольким запускам не удалось сходиться для некоторых алгоритмов, поэтому только лучшие 75% запусков из каждого алгоритма использовались, чтобы получить статистику.
Алгоритмы метода сопряженных градиентов и устойчивая обратная связь, которую все обеспечивают быстрой сходимости и алгоритму LM, также довольно быстры. Как с набором контрольных данных, алгоритм LM не выполняет также на проблемах распознавания образов, как это делает на проблемах приближения функций.
Алгоритм | Среднее время (время) | Отношение | Min. \times | Максимум время (времена) | Станд. (s) |
|---|---|---|---|---|---|
CGB | 80.27 | 1.00 | 55.07 | 102.31 | 13.17 |
RP | 83.41 | 1.04 | 59.51 | 109.39 | 13.44 |
SCG | 86.58 | 1.08 | 41.21 | 112.19 | 18.25 |
CGP | 87.70 | 1.09 | 56.35 | 116.37 | 18.03 |
CGF | 110.05 | 1.37 | 63.33 | 171.53 | 30.13 |
LM | 110.33 | 1.37 | 58.94 | 201.07 | 38.20 |
BFG | 209.60 | 2.61 | 118.92 | 318.18 | 58.44 |
GDX | 313.22 | 3.90 | 166.48 | 446.43 | 75.44 |
OSS | 463.87 | 5.78 | 250.62 | 599.99 | 97.35 |
Следующая фигура строит среднеквадратичную погрешность по сравнению со временем выполнения для некоторых типичных алгоритмов. Для этой проблемы нет такого же изменения эффективности как предыдущих проблем.
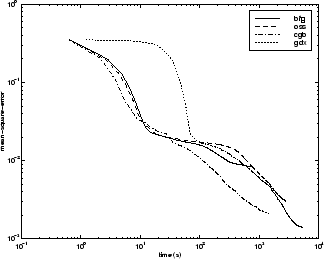
Отношение между алгоритмами далее проиллюстрировано в следующем рисунке, который строит время, требуемое сходиться по сравнению с целью сходимости среднеквадратичной погрешности. Снова вы видите, что некоторые алгоритмы ухудшаются, когда ошибочная цель уменьшается (OSS и BFG), в то время как алгоритм LM улучшается. Это типично для алгоритма LM на любой проблеме, которую ее эффективность улучшает относительно других алгоритмов, когда ошибочная цель уменьшается.
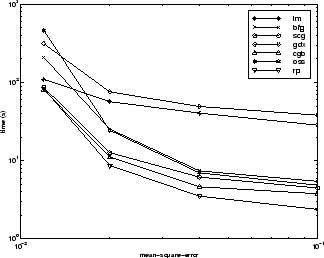
Пятая эталонная тестовая задача является реалистическим приближением функций (или нелинейная регрессия) проблема. Цель сети состоит в том, чтобы предсказать уровни холестерина (ldl, hdl, и vldl) на основе измерений 21 спектрального компонента. Данные были получены от доктора Нила Перди, Отдела Химии, Университета штата Оклахома [PuLu92]. Сеть, используемая для этой проблемы, является 21-15-3 сетями с tansig нейронами в скрытых слоях и линейными нейронами в выходном слое. Следующая таблица обобщает результаты обучения этой сети с девятью различными алгоритмами. Каждая запись в таблице представляет 20 различных испытаний (10 испытаний за RP и GDX), где различные случайные начальные веса используются в каждом испытании. В каждом случае обучена сеть, пока квадратичная невязка не меньше 0.027.
Масштабированный алгоритм метода сопряженных градиентов имеет лучшую эффективность на этой проблеме, несмотря на то, что все алгоритмы метода сопряженных градиентов выполняют хорошо. Алгоритм LM не выполняет также на этой проблеме приближения функций, как это сделало на других двух. Это вызвано тем, что количество весов и смещений в сети увеличилось снова (378 по сравнению с 152 по сравнению с 16). Как количество увеличений параметров, расчет, требуемый в алгоритме LM, увеличивается геометрически.
Алгоритм | Среднее время (время) | Отношение | Min. \times | Максимум время (времена) | Станд. (s) |
|---|---|---|---|---|---|
SCG | 99.73 | 1.00 | 83.10 | 113.40 | 9.93 |
CGP | 121.54 | 1.22 | 101.76 | 162.49 | 16.34 |
CGB | 124.06 | 1.2 | 107.64 | 146.90 | 14.62 |
CGF | 136.04 | 1.36 | 106.46 | 167.28 | 17.67 |
LM | 261.50 | 2.62 | 103.52 | 398.45 | 102.06 |
OSS | 268.55 | 2.69 | 197.84 | 372.99 | 56.79 |
BFG | 550.92 | 5.52 | 471.61 | 676.39 | 46.59 |
RP | 1519.00 | 15.23 | 581.17 | 2256.10 | 557.34 |
GDX | 3169.50 | 31.78 | 2514.90 | 4168.20 | 610.52 |
Следующая фигура строит среднеквадратичную погрешность по сравнению со временем выполнения для некоторых типичных алгоритмов. Для этой проблемы вы видите, что алгоритм LM может управлять среднеквадратичной погрешностью к более низкому уровню, чем другие алгоритмы. SCG и алгоритмы RP обеспечивают самую быструю начальную сходимость.
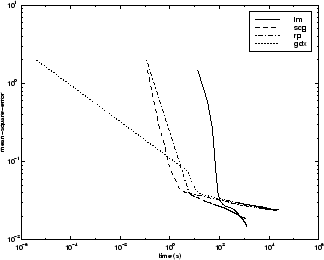
Отношение между алгоритмами далее проиллюстрировано в следующем рисунке, который строит время, требуемое сходиться по сравнению с целью сходимости среднеквадратичной погрешности. Вы видите, что LM и алгоритмы BFG улучшаются относительно других алгоритмов, когда ошибочная цель уменьшается.

Шестая эталонная тестовая задача является проблемой распознавания образов. Цель сети состоит в том, чтобы решить, есть ли у индивидуума диабет, на основе персональных данных (возраст, беременное число раз) и результаты медицинских обследований (e.g., артериальное давление, индекс массы тела, результат теста допуска глюкозы, и т.д.). Данные были получены из Калифорнийского университета, Ирвина, базы данных машинного обучения. Сеть, используемая для этой проблемы, является 8-15-15-2 сетями с tansig нейронами во всех слоях. Следующая таблица обобщает результаты обучения этой сети с девятью различными алгоритмами. Каждая запись в таблице представляет 10 различных испытаний, где различные случайные начальные веса используются в каждом испытании. В каждом случае обучена сеть, пока квадратичная невязка не меньше 0.05.
Алгоритмы метода сопряженных градиентов и устойчивая обратная связь все обеспечивают быструю сходимость. Результаты на этой проблеме сопоставимы с другими рассмотренными задачами распознавания образов. Алгоритм RP работает хорошо над всеми проблемами распознавания образов. Это разумно, потому что тот алгоритм был спроектирован, чтобы преодолеть трудности, вызванные обучением с сигмоидальными функциями, которые имеют очень маленькие наклоны при работе далекий от центральной точки. Для проблем распознавания образов вы используете сигмоидальные передаточные функции в выходном слое, и вы хотите, чтобы сеть действовала в хвостах сигмоидальной функции.
Алгоритм | Среднее время (время) | Отношение | Min. \times | Максимум время (времена) | Станд. (s) |
|---|---|---|---|---|---|
RP | 323.90 | 1.00 | 187.43 | 576.90 | 111.37 |
SCG | 390.53 | 1.21 | 267.99 | 487.17 | 75.07 |
CGB | 394.67 | 1.22 | 312.25 | 558.21 | 85.38 |
CGP | 415.90 | 1.28 | 320.62 | 614.62 | 94.77 |
OSS | 784.00 | 2.42 | 706.89 | 936.52 | 76.37 |
CGF | 784.50 | 2.42 | 629.42 | 1082.20 | 144.63 |
LM | 1028.10 | 3.17 | 802.01 | 1269.50 | 166.31 |
BFG | 1821.00 | 5.62 | 1415.80 | 3254.50 | 546.36 |
GDX | 7687.00 | 23.73 | 5169.20 | 10350.00 | 2015.00 |
Следующая фигура строит среднеквадратичную погрешность по сравнению со временем выполнения для некоторых типичных алгоритмов. Как с другими проблемами, вы видите, что SCG и RP имеют быструю начальную сходимость, в то время как алгоритм LM может обеспечить меньшую конечную погрешность.
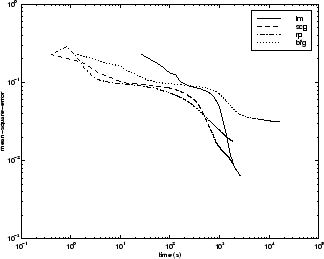
Отношение между алгоритмами далее проиллюстрировано в следующем рисунке, который строит время, требуемое сходиться по сравнению с целью сходимости среднеквадратичной погрешности. В этом случае вы видите, что алгоритм Большого и доброго великана ухудшается, когда ошибочная цель уменьшается, в то время как алгоритм LM улучшается. Алгоритм RP является лучшим, кроме в самой маленькой ошибочной цели, где SCG лучше.
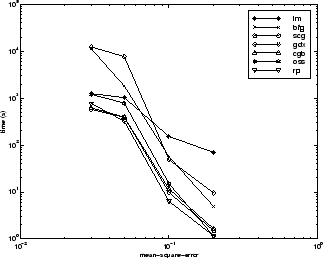
Существует несколько характеристик алгоритма, которые могут быть выведены из описанных экспериментов. В общем случае на проблемах приближения функций, для сетей, которые содержат до нескольких сотен весов, алгоритм Levenberg-Marquardt будет иметь самую быструю сходимость. Это преимущество особенно примечательно, если очень точное обучение требуется. Во многих случаях, trainlm может получить более низкие среднеквадратичные погрешности, чем любой из других протестированных алгоритмов. Однако как количество весов в сетевых увеличениях, преимуществе trainlm уменьшения. Кроме того, trainlm эффективность относительно плоха на проблемах распознавания образов. Требования устройства хранения данных trainlm больше, чем другие протестированные алгоритмы.
trainrp функция является самым быстрым алгоритмом на проблемах распознавания образов. Однако это не выполняет хорошо на проблемах приближения функций. Его эффективность также ухудшается, когда ошибочная цель уменьшается. Требования к памяти для этого алгоритма относительно малы по сравнению с другими рассмотренными алгоритмами.
Алгоритмы метода сопряженных градиентов, в частности trainscg, кажется, выполняю хорошо по большому разнообразию проблем, особенно для сетей с большим количеством весов. Алгоритм SCG почти с такой скоростью, как алгоритм LM на проблемах приближения функций (быстрее для больших сетей) и почти с такой скоростью, как trainrp на проблемах распознавания образов. Его эффективность не ухудшается так же быстро как trainrp эффективность делает, когда ошибка уменьшается. Алгоритмы метода сопряженных градиентов имеют относительно скромные требования к памяти.
Эффективность trainbfg похоже на тот из trainlm. Не требуется такого же количества устройства хранения данных как trainlm, но требуемый расчет действительно увеличивается геометрически с размером сети, потому что эквивалент обратной матрицы должен быть вычислен в каждой итерации.
Переменный алгоритм скорости обучения traingdx обычно намного медленнее, чем другие методы и имеет о тех же требованиях устройства хранения данных как trainrp, но это может все еще быть полезно для некоторых проблем. Существуют определенные ситуации, в которых лучше сходиться более медленно. Например, при использовании ранней остановки у вас могут быть противоречивые результаты, если вы используете алгоритм, который сходится слишком быстро. Вы можете промахнуться по точке, в которой минимизирована ошибка на наборе валидации.