Проект NARMA-L2 Нейроконтроллер в Simulink

Нейроконтроллер, описанный в этом разделе, упомянут двумя различными именами: управление линеаризацией обратной связи и управление NARMA-L2. Это упоминается как линеаризация обратной связи, когда модель объекта управления имеет конкретную форму (сопутствующая форма). Это упоминается как управление NARMA-L2, когда модель объекта управления может быть аппроксимирована той же формой. Центральная идея этого типа управления состоит в том, чтобы преобразовать нелинейную системную динамику в линейную динамику путем отмены нелинейности. Этот раздел начинается путем представления сопутствующей системной модели формы и показа, как можно использовать нейронную сеть, чтобы идентифицировать эту модель. Затем это описывает, как идентифицированная модель нейронной сети может использоваться, чтобы разработать контроллер. Это сопровождается примером того, как использовать Блок управления NARMA-L2, который содержится в библиотеке Deep Learning Toolbox™.

Идентификация модели NARMA-L2

Как с прогнозирующим управлением модели, первым шагом в использовании линеаризации обратной связи (или NARMA-L2) управление должно идентифицировать систему, которой будут управлять. Вы обучаете нейронную сеть, чтобы представлять прямую динамику системы. Первый шаг должен выбрать структуру модели, чтобы использовать. Одна стандартная модель, которая используется, чтобы представлять общее дискретное время нелинейные системы, является нелинейной моделью (NARMA) авторегрессивного скользящего среднего значения:

$y (k + d) = N [y (k), y (k - 1), \dots, y (k - n + 1), u (k), u (k - 1), \dots, u (k - n + 1)]$

где u (k) является системным входом, и y (k) является системой выход. Для идентификационной фазы вы могли обучить нейронную сеть, чтобы аппроксимировать нелинейный функциональный N. Это - идентификационная процедура, используемая для Прогнозирующего Контроллера NN.

Если вы хотите, чтобы система выход следовала за некоторой ссылочной траекторией
y (k + d) = _yr (k + d), следующий шаг должен разработать нелинейный контроллер формы:

$u (k) = G [y (k), y (k - 1), \dots, y (k - n + 1), y_{r} (k + d), u (k - 1), \dots, u (k - m + 1)]$

Проблема с использованием этого контроллера состоит в том, что, если вы хотите обучить нейронную сеть, чтобы создать функциональный G, чтобы минимизировать среднеквадратичную погрешность, необходимо использовать динамическую обратную связь ([NaPa91] или [HaJe99]). Это может быть довольно медленно. Одно решение, предложенное Нарендрой и Махопэдхьяи [NaMu97], состоит в том, чтобы использовать аппроксимированные модели, чтобы представлять систему. Контроллер, используемый в этом разделе, основан на NARMA-L2 аппроксимированная модель:

$\begin{matrix} \hat{y} (k + d) = f [y (k), y (k - 1), \dots, y (k - n + 1), u (k - 1), \dots, u (k - m + 1)] \\ + g [y (k), y (k - 1), \dots, y (k - n + 1), u (k - 1), \dots, u (k - m + 1)] \cdot u (k) \end{matrix}$

Эта модель находится в сопутствующей форме, где следующий вход u контроллера (k) не содержится в нелинейности. Преимущество этой формы состоит в том, что можно решить для входа управления, который заставляет систему выход следовать за ссылочным y (k + d) = _yr (k + d). У получившегося контроллера была бы форма

$u (k) = \frac{y_{r} (k + d) - f [y (k), y (k - 1), \dots, y (k - n + 1), u (k - 1), \dots, u (k - n + 1)]}{g [y (k), y (k - 1), \dots, y (k - n + 1), u (k - 1), \dots, u (k - n + 1)]}$

Используя это уравнение непосредственно может вызвать проблемы реализации, потому что необходимо определить вход u управления (k) на основе выхода одновременно, y (k). Так, вместо этого, используйте модель

$\begin{matrix} y (k + d) = f [y (k), y (k - 1), \dots, y (k - n + 1), u (k), u (k - 1), \dots, u (k - n + 1)] \\ + g [y (k), \dots, y (k - n + 1), u (k), \dots, u (k - n + 1)] \cdot u (k + 1) \end{matrix}$

где d ≥ 2. Следующий рисунок показывает структуру представления нейронной сети.

Контроллер NARMA-L2

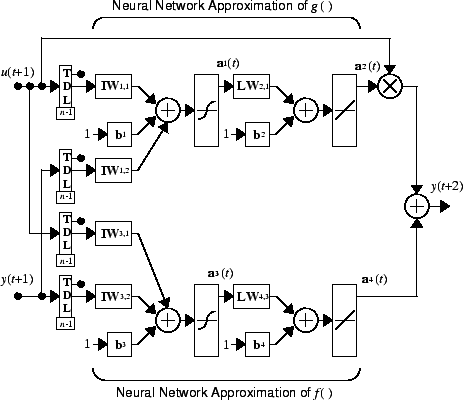
Используя модель NARMA-L2, можно получить контроллер

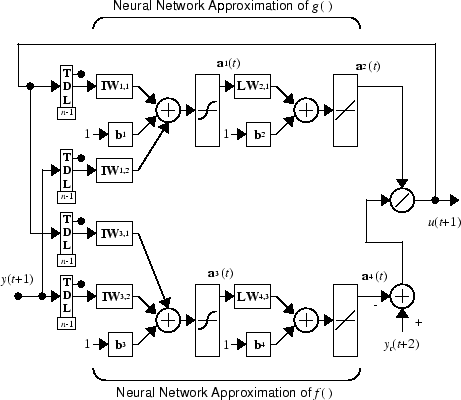
$u (k + 1) = \frac{y_{r} (k + d) - f [y (k), \dots, y (k - n + 1), u (k), \dots, u (k - n + 1)]}{g [y (k), \dots, y (k - n + 1), u (k), \dots, u (k - n + 1)]}$

который осуществим для d ≥ 2. Следующая фигура является блок-схемой контроллера NARMA-L2.

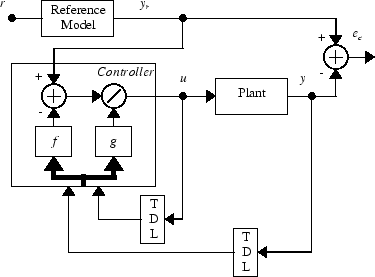
Этот контроллер может быть реализован с ранее идентифицированной моделью объекта управления NARMA-L2 как показано в следующем рисунке.

Используйте блок контроллера NARMA-L2

Этот раздел показывает, как диспетчер NARMA-L2 обучен. Первый шаг должен скопировать блок NARMA-L2 Controller от библиотеки блоков Deep Learning Toolbox до Simulink^® Редактор. См. документацию Simulink, если вы не уверены, как сделать это. Этот шаг пропущен в следующем примере.

Модели в качестве примера предоставляют программное обеспечение Deep Learning Toolbox, чтобы показать использование контроллера NARMA-L2. В этом примере цель состоит в том, чтобы управлять положением магнита, приостановленного выше электромагнита, где магнит ограничивается так, чтобы это могло только переместиться в вертикальное направление, как в следующем рисунке.

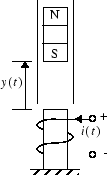
Уравнение движения для этой системы

$\frac{d^{2} y (t)}{d t^{2}} = - g + \frac{α}{M} \frac{i^{2} (t)}{y (t)} - \frac{β}{M} \frac{d y (t)}{d t}$

где y (t) является расстоянием магнита выше электромагнита, i (t) является текущим течением в электромагните, M является массой магнита, и g является ускорением свободного падения. Параметр β является коэффициентом вязкого трения, который определяется материалом, в который перемещается магнит, и α является полевой силой, постоянной, который определяется количеством поворотов провода на электромагните и силе магнита.

Запускать этот пример:

StartMatlab^®.
Введите narmamaglev в командном окне MATLAB. Эта команда открывает Редактор Simulink со следующей моделью. Блок управления NARMA-L2 уже находится в модели.
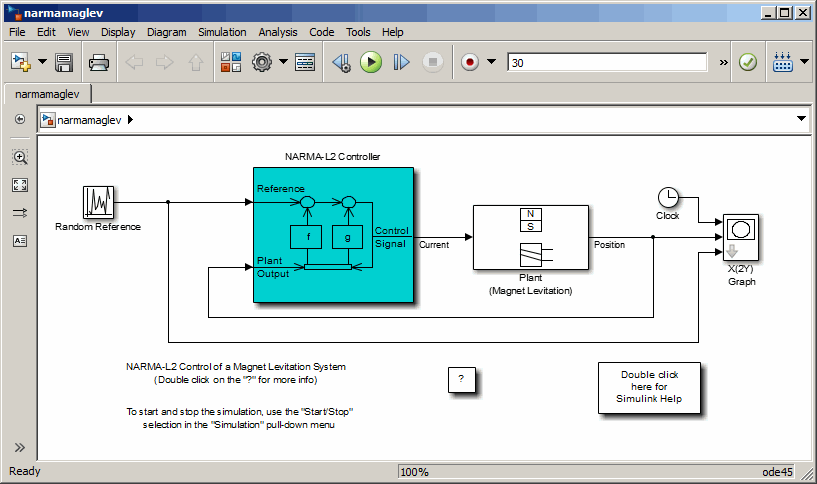
Дважды кликните блок NARMA-L2 Controller. Это открывает следующее окно. Это окно позволяет вам обучить модель NARMA-L2. Нет никакого отдельного окна для контроллера, потому что контроллер определяется непосредственно из модели, в отличие от прогнозирующего контроллера модели.
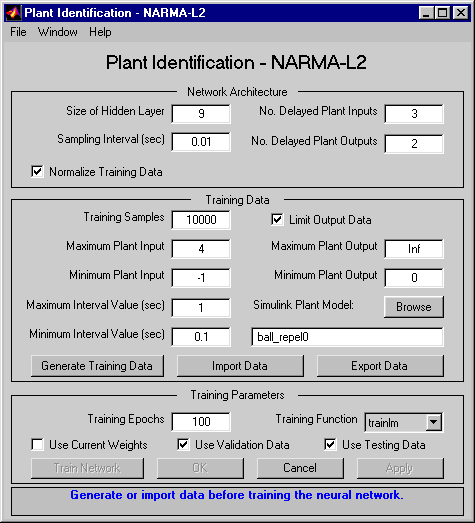
Это окно работает то же самое другими окнами Plant Identification, таким образом, учебный процесс не повторяется. Вместо этого симулируйте контроллер NARMA-L2.
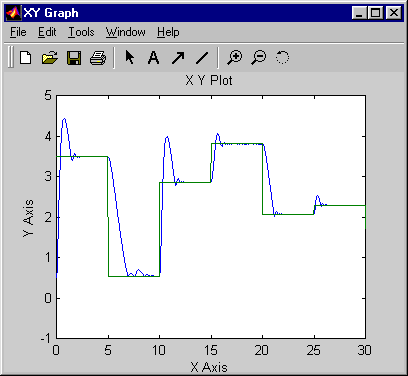
Возвратитесь к Редактору Simulink и запустите симуляцию путем выбора пункта меню Simulation> Run. Когда симуляция запускается, объект, выход и опорный сигнал отображены, как в следующем рисунке.

Документация