simulate

Симулируйте содействующую и инновационную ковариационную матрицу Байесовой векторной модели (VAR) авторегрессии

Синтаксис

[Coeff,Sigma]
= simulate(PriorMdl)

[Coeff,Sigma]
= simulate(PriorMdl,Y)

[Coeff,Sigma]
= simulate(___,Name,Value)

Описание

пример

[Coeff,Sigma] = simulate(PriorMdl) возвращает случайный вектор из коэффициентов Coeff и случайная инновационная ковариационная матрица Sigma чертивший из предшествующей модели Bayesian VAR (p) PriorMdl.

пример

[Coeff,Sigma] = simulate(PriorMdl,Y) чертит от апостериорных распределений, произведенных или обновленных путем слияния данных об ответе Y.

NaNs в данных указывают на отсутствующие значения, который simulate удаляет при помощи мудрого списком удаления.

пример

[Coeff,Sigma] = simulate(___,Name,Value) задает опции с помощью одного или нескольких аргументов пары "имя-значение" в дополнение к любой из комбинаций входных аргументов в предыдущих синтаксисах. Например, можно определить номер случайных ничьих от распределения или задать преддемонстрационные данные об ответе.

Примеры

свернуть все

Чертите содействующую и инновационную ковариационную матрицу от предшествующего распределения

Скрипт Open Live Script

Рассмотрите 3-D модель VAR (4) для инфляции США (INFL), безработица (UNRATE), и федеральные фонды (FEDFUNDS) уровни.

$[\begin{array}{llllllllllllllllllll} {INFL}_{t} \\ {UNRATE}_{t} \\ {FEDFUNDS}_{t} \end{array}] = c + \sum_{j = 1}^{4} Φ_{j} [\begin{array}{llllllllllllllllllll} {INFL}_{t - j} \\ {UNRATE}_{t - j} \\ {FEDFUNDS}_{t - j} \end{array}] + [\begin{array}{cccccccccccccccccccc} ε_{1, t} \\ ε_{2, t} \\ ε_{3, t} \end{array}] .$

\forall $t$ , $ε_{t}$ серия независимых 3-D нормальных инноваций со средним значением 0 и ковариация $Σ$ . Примите что сопряженное предшествующее распределение $π ({[Φ_{1}, . . ., Φ_{4}, c]}^{'}, Σ)$ управляет поведением параметров.

Создайте сопряженную предшествующую модель. Задайте серийные имена ответа. Получите сводные данные предшествующего распределения.

seriesnames = ["INFL" "UNRATE" "FEDFUNDS"];
numseries = numel(seriesnames);
numlags = 4;

PriorMdl = bayesvarm(numseries,numlags,'ModelType','conjugate',...
    'SeriesNames',seriesnames);
Summary = summarize(PriorMdl,'off');

Чертите набор коэффициентов и инновационной ковариационной матрицы от предшествующего распределения.

rng(1) % For reproducibility
[Coeff,Sigma] = simulate(PriorMdl);

Отобразите выбранные коэффициенты с соответствующими именами и инновационной ковариационной матрицей.

table(Coeff,'RowNames',Summary.CoeffMap)

ans=39×1 table
                     Coeff   
                   __________

    AR{1}(1,1)        0.44999
    AR{1}(1,2)       0.047463
    AR{1}(1,3)      -0.042106
    AR{2}(1,1)     -0.0086264
    AR{2}(1,2)       0.034049
    AR{2}(1,3)      -0.058092
    AR{3}(1,1)      -0.015698
    AR{3}(1,2)      -0.053203
    AR{3}(1,3)      -0.031138
    AR{4}(1,1)       0.036431
    AR{4}(1,2)      -0.058279
    AR{4}(1,3)       -0.02195
    Constant(1)        -1.001
    AR{1}(2,1)      -0.068182
    AR{1}(2,2)        0.51029
    AR{1}(2,3)      -0.094367
      ⋮

AR{r} (j, k) является коэффициентом AR переменной отклика k (изолировал r модули), в ответ уравнение j.

Sigma

Sigma = 3×3

    0.1238   -0.0053   -0.0369
   -0.0053    0.0456    0.0160
   -0.0369    0.0160    0.1039

Строки и столбцы Sigma соответствуйте инновациям в уравнениях ответа, упорядоченных PriorMdl.SeriesNames.

Симулируйте параметры от аналитически послушного апостериорного распределения

Скрипт Open Live Script

Рассмотрите 3-D модель VAR (4) Содействующей и Инновационной Ковариационной матрицы Ничьей от Предшествующего Распределения. В этом случае примите, что предшествующее распределение является рассеянным.

Загрузите и предварительно обработайте данные

Загрузите США макроэкономический набор данных. Вычислите уровень инфляции, стабилизируйте показатели безработицы и ставки по федеральным фондам, и удалите отсутствующие значения.

load Data_USEconModel
seriesnames = ["INFL" "UNRATE" "FEDFUNDS"];
DataTable.INFL = 100*[NaN; price2ret(DataTable.CPIAUCSL)];

DataTable.DUNRATE = [NaN; diff(DataTable.UNRATE)];
DataTable.DFEDFUNDS = [NaN; diff(DataTable.FEDFUNDS)];
seriesnames(2:3) = "D" + seriesnames(2:3);
rmDataTable = rmmissing(DataTable);

Создайте предшествующую модель

Создайте рассеянный Байесов VAR (4) предшествующая модель для трех рядов ответа. Задайте серийные имена ответа.

numseries = numel(seriesnames);
numlags = 4;

PriorMdl = bayesvarm(numseries,numlags,'SeriesNames',seriesnames);

Оцените апостериорное распределение

Оцените апостериорное распределение. Возвратите сводные данные оценки.

[PosteriorMdl,Summary] = estimate(PriorMdl,rmDataTable{:,seriesnames});

Bayesian VAR under diffuse priors
Effective Sample Size:          197
Number of equations:            3
Number of estimated Parameters: 39
             |   Mean     Std  
-------------------------------
 Constant(1) |  0.1007  0.0832 
 Constant(2) | -0.0499  0.0450 
 Constant(3) | -0.4221  0.1781 
 AR{1}(1,1)  |  0.1241  0.0762 
 AR{1}(2,1)  | -0.0219  0.0413 
 AR{1}(3,1)  | -0.1586  0.1632 
 AR{1}(1,2)  | -0.4809  0.1536 
 AR{1}(2,2)  |  0.4716  0.0831 
 AR{1}(3,2)  | -1.4368  0.3287 
 AR{1}(1,3)  |  0.1005  0.0390 
 AR{1}(2,3)  |  0.0391  0.0211 
 AR{1}(3,3)  | -0.2905  0.0835 
 AR{2}(1,1)  |  0.3236  0.0868 
 AR{2}(2,1)  |  0.0913  0.0469 
 AR{2}(3,1)  |  0.3403  0.1857 
 AR{2}(1,2)  | -0.0503  0.1647 
 AR{2}(2,2)  |  0.2414  0.0891 
 AR{2}(3,2)  | -0.2968  0.3526 
 AR{2}(1,3)  |  0.0450  0.0413 
 AR{2}(2,3)  |  0.0536  0.0223 
 AR{2}(3,3)  | -0.3117  0.0883 
 AR{3}(1,1)  |  0.4272  0.0860 
 AR{3}(2,1)  | -0.0389  0.0465 
 AR{3}(3,1)  |  0.2848  0.1841 
 AR{3}(1,2)  |  0.2738  0.1620 
 AR{3}(2,2)  |  0.0552  0.0876 
 AR{3}(3,2)  | -0.7401  0.3466 
 AR{3}(1,3)  |  0.0523  0.0428 
 AR{3}(2,3)  |  0.0008  0.0232 
 AR{3}(3,3)  |  0.0028  0.0917 
 AR{4}(1,1)  |  0.0167  0.0901 
 AR{4}(2,1)  |  0.0285  0.0488 
 AR{4}(3,1)  | -0.0690  0.1928 
 AR{4}(1,2)  | -0.1830  0.1520 
 AR{4}(2,2)  | -0.1795  0.0822 
 AR{4}(3,2)  |  0.1494  0.3253 
 AR{4}(1,3)  |  0.0067  0.0395 
 AR{4}(2,3)  |  0.0088  0.0214 
 AR{4}(3,3)  | -0.1372  0.0845 
       Innovations Covariance Matrix       
           |   INFL     DUNRATE  DFEDFUNDS 
-------------------------------------------
 INFL      |  0.3028   -0.0217     0.1579  
           | (0.0321)  (0.0124)   (0.0499) 
 DUNRATE   | -0.0217    0.0887    -0.1435  
           | (0.0124)  (0.0094)   (0.0283) 
 DFEDFUNDS |  0.1579   -0.1435     1.3872  
           | (0.0499)  (0.0283)   (0.1470)

PosteriorMdl conjugatebvarm модель, которая аналитически послушна.

Симулируйте параметры от следующего

Чертите 1 000 выборок от апостериорного распределения.

rng(1)
[Coeff,Sigma] = simulate(PosteriorMdl,'NumDraws',1000);

Coeff 39 1000 матрица случайным образом чертивших коэффициентов. Каждый столбец является отдельной ничьей, и каждая строка является отдельным коэффициентом. Sigma 3 3 1 000 массивов случайным образом чертивших инновационных ковариационных матриц. Каждая страница является отдельной ничьей.

Отобразите первый коэффициент, чертивший от распределения с соответствующими названиями параметра, и отобразите первую чертившую инновационную ковариационную матрицу.

Coeffs = table(Coeff(:,1),'RowNames',Summary.CoeffMap)

Coeffs=39×1 table
                     Var1   
                   _________

    AR{1}(1,1)       0.14994
    AR{1}(1,2)      -0.46927
    AR{1}(1,3)      0.088388
    AR{2}(1,1)       0.28139
    AR{2}(1,2)      -0.19597
    AR{2}(1,3)      0.049222
    AR{3}(1,1)        0.3946
    AR{3}(1,2)      0.081871
    AR{3}(1,3)      0.002117
    AR{4}(1,1)       0.13514
    AR{4}(1,2)      -0.23661
    AR{4}(1,3)      -0.01869
    Constant(1)     0.035787
    AR{1}(2,1)     0.0027895
    AR{1}(2,2)       0.62382
    AR{1}(2,3)      0.053232
      ⋮

Sigma(:,:,1)

ans = 3×3

    0.2653   -0.0075    0.1483
   -0.0075    0.1015   -0.1435
    0.1483   -0.1435    1.5042

Симулируйте параметры от аналитически тяжелого апостериорного распределения

Скрипт Open Live Script

Загрузите и предварительно обработайте данные

load Data_USEconModel
seriesnames = ["INFL" "UNRATE" "FEDFUNDS"];
DataTable.INFL = 100*[NaN; price2ret(DataTable.CPIAUCSL)];

DataTable.DUNRATE = [NaN; diff(DataTable.UNRATE)];
DataTable.DFEDFUNDS = [NaN; diff(DataTable.FEDFUNDS)];
seriesnames(2:3) = "D" + seriesnames(2:3);
rmDataTable = rmmissing(DataTable);

Создайте предшествующую модель

Создайте полусопряженный Байесов VAR (4) предшествующая модель для трех рядов ответа. Задайте имена переменной отклика.

numseries = numel(seriesnames);
numlags = 4;

PriorMdl = bayesvarm(numseries,numlags,'Model','semiconjugate',...
    'SeriesNames',seriesnames);

Симулируйте параметры от следующего

Поскольку объединенное апостериорное распределение полусопряженной предшествующей модели аналитически тяжело, simulate последовательно чертит от полных условных распределений.

Чертите 1 000 выборок от апостериорного распределения. Задайте электротермотренировку 10 000 и утончающийся фактор 5. Запустите сэмплер Гиббса путем принятия следующего среднего значения $Σ$ 3-D единичная матрица.

rng(1)
[Coeff,Sigma] = simulate(PriorMdl,rmDataTable{:,seriesnames},...
    'NumDraws',1000,'BurnIn',1e4,'Thin',5,'Sigma0',eye(3));

Симулируйте коэффициенты из модели VARX

Скрипт Open Live Script

Считайте 2D модель VARX(1) для США действительным GDP (RGDP) и инвестиции (GCE) уровни, который обрабатывает персональное потребление (PCEC) уровень как внешний:

$[\begin{array}{llllllllllllllllllll} {RGDP}_{t} \\ {GCE}_{t} \end{array}] = c + Φ [\begin{array}{llllllllllllllllllll} {RGDP}_{t - 1} \\ {GCE}_{t - 1} \end{array}] + {PCEC}_{t} β + ε_{t} .$

\forall $t$ , $ε_{t}$ серия независимых 2D нормальных инноваций со средним значением 0 и ковариация $Σ$ . Примите следующие предшествующие распределения:

${[\begin{array}{c} Φ & c & β \end{array}]}^{'} | Σ \sim Ν_{4 \times 2} (Μ, V, Σ)$ , где M 4 2 матрица средних значений и $V$ матрица шкалы среди коэффициента 4 на 4. Эквивалентно, $vec ({[\begin{array}{c} Φ & c & β \end{array}]}^{'}) | Σ \sim Ν_{8} (vec (Μ), Σ \otimes V)$ .
$Σ \sim I n v e r s e W i s h a r t (Ω, ν),$ где Ω является матрицей шкалы 2 на 2 и $ν$ степени свободы.

Загрузите США макроэкономический набор данных. Вычислите действительный GDP, инвестиции и персональный ряд нормы потребления. Удалите все отсутствующие значения из получившегося ряда.

load Data_USEconModel
DataTable.RGDP = DataTable.GDP./DataTable.GDPDEF;
seriesnames = ["PCEC"; "RGDP"; "GCE"];
rates = varfun(@price2ret,DataTable,'InputVariables',seriesnames);
rates = rmmissing(rates);
rates.Properties.VariableNames = seriesnames;

Создайте сопряженную предшествующую модель для 2D VARX (1) параметры модели.

numseries = 2;
numlags = 1;
numpredictors = 1;
PriorMdl = conjugatebvarm(numseries,numlags,'NumPredictors',numpredictors,...
    'SeriesNames',seriesnames(2:end));

Симулируйте непосредственно от апостериорного распределения. Задайте внешние данные о предикторе.

[Coeff,Sigma] = simulate(PriorMdl,rates{:,PriorMdl.SeriesNames},...
    'X',rates{:,seriesnames(1)});

По умолчанию, simulate использует первый p = 1 наблюдение за данными об ответе, чтобы инициализировать динамический компонент модели и удаляет соответствующие наблюдения из данных о предикторе.

Входные параметры

свернуть все

`PriorMdl` — Предшествующая модель Bayesian VAR
`conjugatebvarm` объект модели | `semiconjugatebvarm` объект модели | `diffusebvarm` объект модели | `normalbvarm` объект модели

Предшествующая модель Bayesian VAR в виде объекта модели в этой таблице.

Объект модели	Описание
`conjugatebvarm`	Зависимый, матричная нормальная инверсия Уишарт спрягают модель, возвращенную `bayesvarm` или `conjugatebvarm`
`semiconjugatebvarm`	Независимый, нормальный обратный Уишарт полуспрягает предшествующую модель, возвращенную `bayesvarm` или `semiconjugatebvarm`
`diffusebvarm`	Рассейте предшествующую модель, возвращенную `bayesvarm` или `diffusebvarm`
`normalbvarm`	Нормальная сопряженная модель с фиксированной инновационной ковариационной матрицей, возвращенной `bayesvarm` или `normalbvarm`

Примечание

Если PriorMdl diffusebvarm модель, затем необходимо также предоставить Y потому что simulate не может чертить от неподходящего предшествующего распределения. Следовательно, Coeff и Sigma представляйте чертит от апостериорного распределения.

`Y` — Наблюдаемый многомерный ряд ответа
числовая матрица

Наблюдаемый многомерный ряд ответа, к который simulate подбирает модель в виде numobs- numseries числовая матрица.

numobs объем выборки. numseries количество переменных отклика (PriorMdl.NumSeries).

Строки соответствуют наблюдениям, и последняя строка содержит последнее наблюдение. Столбцы соответствуют отдельным переменным отклика.

Y представляет продолжение преддемонстрационного ряда ответа в Y0.

Типы данных: double

Аргументы name-value

Задайте дополнительные разделенные запятой пары Name,Value аргументы. Name имя аргумента и Value соответствующее значение. Name должен появиться в кавычках. Вы можете задать несколько аргументов в виде пар имен и значений в любом порядке, например: Name1, Value1, ..., NameN, ValueN.

Пример: 'Y0',Y0,'X',X задает преддемонстрационные данные об ответе Y0 инициализировать модель VAR для следующей оценки и данные о предикторе X для внешнего компонента регрессии.

Опции для всех предшествующих распределений

свернуть все

`NumDraws` — Количество случайных ничьих
1 (значение по умолчанию) | положительное целое число

Количество случайных ничьих от распределений в виде разделенной запятой пары, состоящей из 'NumDraws' и положительное целое число.

Пример: 'NumDraws',1e7

Типы данных: double

`Y0` — Преддемонстрационные данные об ответе
числовая матрица

Преддемонстрационные данные об ответе, чтобы инициализировать модель VAR для оценки в виде разделенной запятой пары, состоящей из 'Y0' и numpreobs- numseries числовая матрица. numpreobs количество преддемонстрационных наблюдений.

Строки соответствуют преддемонстрационным наблюдениям, и последняя строка содержит последнее наблюдение. Y0 должен иметь, по крайней мере, PriorMdl.P 'Строки' . Если вы предоставляете больше строк, чем необходимый, simulate использует последний PriorMdl.P наблюдения только.

Столбцы должны соответствовать ряду ответа в Y.

По умолчанию, simulate использование Y(1:PriorMdl.P,:) как преддемонстрационные наблюдения, и затем оценивает следующее использование Y((PriorMdl.P + 1):end,:). Это действие уменьшает эффективный объем выборки.

Типы данных: double

`X` — Данные о предикторе
числовая матрица

Данные о предикторе для внешнего компонента регрессии в модели в виде разделенной запятой пары, состоящей из 'X' и numobs- PriorMdl.NumPredictors числовая матрица.

Строки соответствуют наблюдениям, и последняя строка содержит последнее наблюдение. simulate не использует компонент регрессии в преддемонстрационный период. X должен иметь, по крайней мере, столько наблюдений, сколько наблюдения использовали после преддемонстрационного периода.

Если вы задаете Y0, затем X должен иметь, по крайней мере, numobs строки (см. Y).
В противном случае, X должен иметь, по крайней мере, numobs – PriorMdl.P наблюдения с учетом преддемонстрационного удаления.

В любом случае, если вы предоставляете больше строк, чем необходимый, simulate использует последние наблюдения только.

Столбцы соответствуют отдельным переменным предикторам. Все переменные предикторы присутствуют в компоненте регрессии каждого уравнения ответа.

Типы данных: double

Опции для полусопряженных предшествующих распределений

свернуть все

`BurnIn` — Количество ничьих, чтобы удалить с начала выборки
0 (значение по умолчанию) | неотрицательный скаляр

Количество ничьих, чтобы удалить с начала выборки уменьшать переходные эффекты в виде разделенной запятой пары, состоящей из 'BurnIn' и неотрицательный скаляр. Для получения дополнительной информации, на как simulate уменьшает полную выборку, см. Алгоритмы.

Совет

Помочь вам задать соответствующий размер электротермотренировки:

Определите степень переходного поведения в выборке путем определения 'BurnIn',0.
Симулируйте несколько тысяч наблюдений при помощи simulate.
Постройте графики трассировки.

Пример: 'BurnIn',0

Типы данных: double

`Thin` — Настроенный множитель объема выборки
1 (значение по умолчанию) | положительное целое число

Настроенный множитель объема выборки в виде разделенной запятой пары, состоящей из 'Thin' и положительное целое число.

Фактическим объемом выборки является BurnIn + NumDraws*Thin. После отбрасывания выжигания дефектов, simulate отбрасывает каждый Thin– 1 чертит, и затем сохраняет следующую ничью. Для получения дополнительной информации о как simulate уменьшает полную выборку, см. Алгоритмы.

Совет

Уменьшать потенциальную большую последовательную корреляцию в выборке или уменьшать потребление памяти ничьих, сохраненных в Coeff и Sigma, задайте большое значение для Thin.

Пример: 'Thin',5

Типы данных: double

`Coeff0` — Начальное значение коэффициентов модели VAR для сэмплера Гиббса
числовой вектор-столбец

Начальное значение коэффициентов модели VAR для сэмплера Гиббса в виде разделенной запятой пары, состоящей из 'Coeff0' и числовой вектор-столбец с (PriorMdl. NumSeries*k)-by-NumDraws элементы, где k = PriorMdl.NumSeries*PriorMdl.P + PriorMdl.IncludeIntercept + PriorMdl.IncludeTrend + PriorMdl.NumPredictors, который является количеством коэффициентов в уравнении ответа. Для получения дополнительной информации на структуре Coeff0, смотрите выход Coeff.

По умолчанию, Coeff0 многомерная оценка наименьших квадратов.

Совет

Задавать Coeff0:
1. Установите отдельные переменные для начальных значений каждая матрица коэффициентов и вектор.
2. Горизонтально конкатенируйте все содействующие средние значения в этом порядке:
  
  $C o e f f = [\begin{matrix} Φ_{1} & Φ_{2} & \dots & Φ_{p} & c & δ & Β \end{matrix}] .$
3. Векторизуйте транспонирование содействующей средней матрицы.
  Coeff0 = Coeff.'; Coeff0 = Coeff0(:);
Хорошая практика должна запуститься simulate многократно с различными начальными значениями параметра. Проверьте, что оценки от каждого запуска сходятся к подобным значениям.

Типы данных: double

`Sigma0` — Начальное значение инновационной ковариационной матрицы для сэмплера Гиббса
положительная определенная числовая матрица

Начальное значение инновационной ковариационной матрицы для сэмплера Гиббса в виде разделенной запятой пары, состоящей из 'Sigma0' и PriorMdl.NumSeries- PriorMdl.NumSeries положительная определенная числовая матрица. По умолчанию, Sigma0 остаточная среднеквадратическая ошибка от многомерных наименьших квадратов. Строки и столбцы соответствуют инновациям в уравнениях переменных отклика, упорядоченных PriorMdl.SeriesNames.

Совет

Хорошая практика должна запуститься simulate многократно с различными начальными значениями параметра. Проверьте, что оценки от каждого запуска сходятся к подобным значениям.

Типы данных: double

Выходные аргументы

свернуть все

`Coeff` — Симулированные коэффициенты модели VAR
числовая матрица

Симулированные коэффициенты модели VAR, возвращенные как (PriorMdl. NumSeries*k)-by-NumDraws числовая матрица, где k = PriorMdl.NumSeries*PriorMdl.P + PriorMdl.IncludeIntercept + PriorMdl.IncludeTrend + PriorMdl.NumPredictors, который является количеством коэффициентов в уравнении ответа. Каждый столбец является отдельной ничьей от распределения.

Для ничьей j, Коэффициент (1:kJ) соответствует всем коэффициентам в уравнении переменной отклика PriorMdl.SeriesNames(1), Коэффициент ((k + 1): (2*kJ) соответствует всем коэффициентам в уравнении переменной отклика PriorMdl.SeriesNames(2), и так далее. Для набора индексов, соответствующих уравнению:

Элементы 1 через PriorMdl.NumSeries соответствуйте задержке 1 коэффициент AR переменных отклика, упорядоченных PriorMdl.SeriesNames.
Элементы PriorMdl.NumSeries + 1 через 2*PriorMdl.NumSeries соответствуйте задержке 2 коэффициента AR переменных отклика, упорядоченных PriorMdl.SeriesNames.
В общем случае элементы (q – 1) *PriorMdl.NumSeries + 1 через q*PriorMdl.NumSeries соответствуйте задержке q Коэффициенты AR переменных отклика упорядочены PriorMdl.SeriesNames.
Если PriorMdl.IncludeConstant true, элемент PriorMdl.NumSeries*PriorMdl.P + 1 константа модели.
Если PriorMdl.IncludeTrend true, элемент PriorMdl.NumSeries*PriorMdl.P + 2 линейный коэффициент тренда времени.
Если PriorMdl.NumPredictors > 0, элементы PriorMdl.NumSeries*PriorMdl.P + 3 через k составьте вектор из коэффициентов регрессии внешних переменных.

Этот рисунок показывает структуру Коэффициента (L, j) для 2D модели VAR (3), которая содержит постоянный вектор и четыре внешних предиктора.

$[\overset{y_{1, t}}{\overset{︷}{\begin{matrix} ϕ_{1, 11} & ϕ_{1, 12} & ϕ_{2, 11} & ϕ_{2, 12} & ϕ_{3, 11} & ϕ_{3, 12} & c_{1} & β_{11} & β_{12} & β_{13} & β_{14} \end{matrix}}} \overset{y_{2, t}}{\overset{︷}{\begin{matrix} ϕ_{1, 21} & ϕ_{1, 22} & ϕ_{2, 21} & ϕ_{2, 22} & ϕ_{3, 21} & ϕ_{3, 22} & c_{2} & β_{21} & β_{22} & β_{23} & β_{24} \end{matrix}}}],$

где

ϕ _{q, jk} является элементом (j, k) задержки матрица коэффициентов AR q.
c _j является константой модели в уравнении переменной отклика j.
B _{j u} является коэффициентом регрессии внешней переменной u в уравнении переменной отклика j.

`Sigma` — Симулированные инновационные ковариационные матрицы
массив положительных определенных числовых матриц

Симулированные инновационные ковариационные матрицы, возвращенные как PriorMdl.NumSeries- PriorMdl.NumSeries- NumDraws массив положительных определенных числовых матриц.

Каждая страница является отдельной ничьей (ковариация) от распределения. Строки и столбцы соответствуют инновациям в уравнениях переменных отклика, упорядоченных PriorMdl.SeriesNames.

Если PriorMdl normalbvarm объект, все ковариации в Sigma равны PriorMdl.Covariance.

Ограничения

simulate не может чертить значения от improper distribution, который является распределением, плотность которого не объединяется к 1.

Больше о

свернуть все

Байесова векторная авторегрессия (VAR) модель

Bayesian VAR model обрабатывает все коэффициенты и инновационную ковариационную матрицу как случайные переменные в m - размерная, стационарная модель VARX(p). Модель имеет одну из трех форм, описанных в этой таблице.

Модель	Уравнение
VAR уменьшаемой формы (p) в обозначении разностного уравнения	$y_{t} = Φ_{1} y_{t - 1} + ... + Φ_{p} y_{t - p} + c + δ t + Β x_{t} + ε_{t} .$
Многомерная регрессия	$y_{t} = Z_{t} λ + ε_{t} .$
Матричная регрессия	$y_{t} = Λ^{'} z_{t}^{'} + ε_{t} .$

В течение каждого раза t = 1..., T:

_yt является m - размерный наблюдаемый вектор отклика, где m = numseries.
_Φ1, …, Φ_p является m-by-m содействующие матрицы AR задержек 1 через p, где p = numlags.
c является m-by-1 вектор из констант модели если IncludeConstant true.
δ является m-by-1 вектор из линейных коэффициентов тренда времени если IncludeTrend true.
Β m-by-r матрица коэффициентов регрессии r-by-1 вектор из наблюдаемых внешних предикторов x _t, где r = NumPredictors. Все переменные предикторы появляются в каждом уравнении.
$z_{t} = [\begin{matrix} y_{t - 1}^{'} & y_{t - 2}^{'} & \dots & y_{t - p}^{'} & 1 & t & x_{t}^{'} \end{matrix}],$ который является 1 на (mp + r + 2) вектор, и Z _t является m-by-m матрица диагонали блока (mp + r + 2)

$[\begin{matrix} z_{t} & 0_{z} & \dots & 0_{z} \\ 0_{z} & z_{t} & \dots & 0_{z} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ 0_{z} & 0_{z} & 0_{z} & z_{t} \end{matrix}],$
где 0_z является 1 на (mp + r + 2) нулевой вектор.
$Λ = {[\begin{matrix} Φ_{1} & Φ_{2} & \dots & Φ_{p} & c & δ & Β \end{matrix}]}^{'}$ , который является (mp + r + 2)-by-m случайная матрица коэффициентов и m (mp + r + 2)-by-1 векторный λ = vec (Λ).
_εt является m-by-1 вектор из случайных, последовательно некоррелированых, многомерных нормальных инноваций с нулевым вектором для среднего значения и m-by-m матрица Σ для ковариации. Это предположение подразумевает, что вероятность данных

$ℓ (Λ, Σ | y, x) = \prod_{t = 1}^{T} f (y_{t}; Λ, Σ, z_{t}),$
где f является m - размерная многомерная нормальная плотность со средним z _t Λ и ковариация Σ, оцененный в y _t.

Прежде, чем рассмотреть данные, вы налагаете предположение joint prior distribution на (Λ,Σ), которым управляет распределение π (Λ,Σ). В Байесовом анализе распределение параметров обновляется с информацией о параметрах, полученных из вероятности данных. Результатом является π joint posterior distribution (Λ,Σ | Y, X, Y ₀), где:

Y является T-by-m матрица, содержащая целый ряд ответа {y _t}, t = 1, …, T.
X является T-by-m матрица, содержащая целый внешний ряд {x _t}, t = 1, …, T.
Y ₀ является p-by-m, матрица преддемонстрационных данных раньше инициализировала модель VAR для оценки.

Советы

Симуляция Монте-Карло подвергается изменению. Если simulate симуляция Монте-Карло использования, затем оценивает, и выводы могут варьироваться, когда вы вызываете simulate многократно при на вид эквивалентных условиях. Чтобы воспроизвести результаты оценки, установите seed случайных чисел при помощи rng перед вызовом simulate.

Алгоритмы

Если simulate оценивает апостериорное распределение (когда вы предоставляете Y) и следующее аналитически послушно, simulate симулирует непосредственно от следующего. В противном случае, simulate использует сэмплер Гиббса, чтобы оценить следующее.
Этот рисунок показывает как simulate уменьшает выборку при помощи значений NumDraws, Thin, и BurnIn. Прямоугольники представляют последовательные ничьи от распределения. simulate удаляет белые прямоугольники из выборки. Остающийся NumDraws черные прямоугольники составляют выборку.
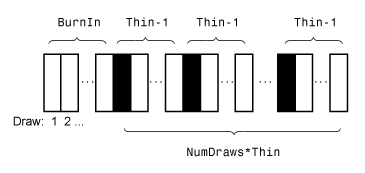
Если PriorMdl semiconjugatebvarm возразите и вы не задаете начальные значения (Coeff0 и Sigma0), simulate выборки от апостериорного распределения путем применения сэмплера Гиббса.
1. simulate использует значение по умолчанию Sigma0 для Σ и чертит значение Λ от π (Λ |Σ, Y, X), полное условное распределение коэффициентов модели VAR.
2. simulate чертит значение Σ от π (Σ |Λ, Y, X), полное условное распределение инновационной ковариационной матрицы, при помощи ранее сгенерированного значения Λ.
3. Функция повторяет шаги 1 и 2 до сходимости. Чтобы оценить сходимость, постройте график трассировки выборки.
Если вы задаете Coeff0, simulate чертит значение Σ от π (Σ |Λ, Y, X), чтобы запустить сэмплер Гиббса.
simulate не возвращает начальные значения по умолчанию, которые это генерирует.

Смотрите также

Объекты

normalbvarm | conjugatebvarm | semiconjugatebvarm | diffusebvarm | empiricalbvarm

Документация

simulate

Синтаксис

Описание

Примеры

Чертите содействующую и инновационную ковариационную матрицу от предшествующего распределения

Симулируйте параметры от аналитически послушного апостериорного распределения

Симулируйте параметры от аналитически тяжелого апостериорного распределения

Симулируйте коэффициенты из модели VARX

Входные параметры

`PriorMdl` — Предшествующая модель Bayesian VAR
`conjugatebvarm` объект модели | `semiconjugatebvarm` объект модели | `diffusebvarm` объект модели | `normalbvarm` объект модели

`Y` — Наблюдаемый многомерный ряд ответа
числовая матрица

Аргументы name-value

`NumDraws` — Количество случайных ничьих
1 (значение по умолчанию) | положительное целое число

`Y0` — Преддемонстрационные данные об ответе
числовая матрица

`X` — Данные о предикторе
числовая матрица

`BurnIn` — Количество ничьих, чтобы удалить с начала выборки
0 (значение по умолчанию) | неотрицательный скаляр

`Thin` — Настроенный множитель объема выборки
1 (значение по умолчанию) | положительное целое число

`Coeff0` — Начальное значение коэффициентов модели VAR для сэмплера Гиббса
числовой вектор-столбец

`Sigma0` — Начальное значение инновационной ковариационной матрицы для сэмплера Гиббса
положительная определенная числовая матрица

Выходные аргументы

`Coeff` — Симулированные коэффициенты модели VAR
числовая матрица

`Sigma` — Симулированные инновационные ковариационные матрицы
массив положительных определенных числовых матриц

Ограничения

Больше о

Байесова векторная авторегрессия (VAR) модель

Советы

Алгоритмы

Смотрите также

Объекты

Функции

Документация Econometrics Toolbox

Поддержка

Документация

simulate

Синтаксис

Описание

Примеры

Чертите содействующую и инновационную ковариационную матрицу от предшествующего распределения

Симулируйте параметры от аналитически послушного апостериорного распределения

Симулируйте параметры от аналитически тяжелого апостериорного распределения

Симулируйте коэффициенты из модели VARX

Входные параметры

PriorMdl — Предшествующая модель Bayesian VAR conjugatebvarm объект модели | semiconjugatebvarm объект модели | diffusebvarm объект модели | normalbvarm объект модели

Y — Наблюдаемый многомерный ряд ответа числовая матрица

Аргументы name-value

NumDraws — Количество случайных ничьих1 (значение по умолчанию) | положительное целое число

Y0 — Преддемонстрационные данные об ответе числовая матрица

X — Данные о предикторе числовая матрица

BurnIn — Количество ничьих, чтобы удалить с начала выборки0 (значение по умолчанию) | неотрицательный скаляр

Thin — Настроенный множитель объема выборки1 (значение по умолчанию) | положительное целое число

Coeff0 — Начальное значение коэффициентов модели VAR для сэмплера Гиббса числовой вектор-столбец

Sigma0 — Начальное значение инновационной ковариационной матрицы для сэмплера Гиббса положительная определенная числовая матрица

Выходные аргументы

Coeff — Симулированные коэффициенты модели VAR числовая матрица

Sigma — Симулированные инновационные ковариационные матрицы массив положительных определенных числовых матриц

Ограничения

Больше о

Байесова векторная авторегрессия (VAR) модель

Советы

Алгоритмы

Смотрите также

Объекты

Функции

Документация Econometrics Toolbox

Поддержка

`PriorMdl` — Предшествующая модель Bayesian VAR
`conjugatebvarm` объект модели | `semiconjugatebvarm` объект модели | `diffusebvarm` объект модели | `normalbvarm` объект модели

`Y` — Наблюдаемый многомерный ряд ответа
числовая матрица

`NumDraws` — Количество случайных ничьих
1 (значение по умолчанию) | положительное целое число

`Y0` — Преддемонстрационные данные об ответе
числовая матрица

`X` — Данные о предикторе
числовая матрица

`BurnIn` — Количество ничьих, чтобы удалить с начала выборки
0 (значение по умолчанию) | неотрицательный скаляр

`Thin` — Настроенный множитель объема выборки
1 (значение по умолчанию) | положительное целое число

`Coeff0` — Начальное значение коэффициентов модели VAR для сэмплера Гиббса
числовой вектор-столбец

`Sigma0` — Начальное значение инновационной ковариационной матрицы для сэмплера Гиббса
положительная определенная числовая матрица

`Coeff` — Симулированные коэффициенты модели VAR
числовая матрица

`Sigma` — Симулированные инновационные ковариационные матрицы
массив положительных определенных числовых матриц