simsmooth

Симуляция, более сглаженная из Байесовой векторной модели (VAR) авторегрессии

Синтаксис

[CoeffDraws,SigmaDraws] = simsmooth(PriorMdl,Y)

[CoeffDraws,SigmaDraws] = simsmooth(PriorMdl,Y,Name,Value)

[CoeffDraws,SigmaDraws,NaNDraws]
= simsmooth(___)

[CoeffDraws,SigmaDraws,NaNDraws,YMean,YStd]
= simsmooth(___)

Описание

simsmooth хорошо подходит для усовершенствованных приложений, таких как условное прогнозирование из выборки от следующего прогнозирующего распределения модели Bayesian VAR (p), прогнозирование модели VARX(p), обвинение отсутствующего значения и оценка параметра в присутствии отсутствующих значений. Кроме того, simsmooth позволяет вам настроить сэмплер Гиббса для прогнозирования из выборки. Чтобы оценить прогнозы из выборки из модели Bayesian VAR (p), смотрите forecast.

пример

[CoeffDraws,SigmaDraws] = simsmooth(PriorMdl,Y) возвращает 1 000 случайных ничьих векторов коэффициентов λ Coeff и инновационные ковариационные матрицы Σ Sigma, чертивший от апостериорного распределения, сформированного путем объединения предшествующей модели Bayesian VAR (p) PriorMdl и данные об ответе Y.

Процедура выборки включает Байесов шаг увеличения данных, который использует Фильтр Калмана (см. Алгоритмы). Во время выборки, simsmooth непреддемонстрационные отсутствующие значения замен в Y, обозначенный NaN значения, с оценочными значениями.

пример

[CoeffDraws,SigmaDraws] = simsmooth(PriorMdl,Y,Name,Value) дополнительные опции использования заданы одним или несколькими аргументами пары "имя-значение". Например, можно определить номер случайных ничьих от распределения или задать преддемонстрационные данные об ответе.

пример

[CoeffDraws,SigmaDraws,NaNDraws] = simsmooth(___) также возвращается, оценочные значения отклика каждого чертят NaNDraws использование любой из комбинаций входных аргументов в предыдущих синтаксисах.

пример

[CoeffDraws,SigmaDraws,NaNDraws,YMean,YStd] = simsmooth(___) также возвращает средний YMean и стандартное отклонение YStd из следующего прогнозирующего распределения увеличенных данных.

Примеры

свернуть все

Симулируйте параметры от апостериорного распределения при наличии отсутствующих значений

Скрипт Open Live Script

Когда simulate оценивает апостериорное распределение, от которого можно чертить параметры, оно удаляет все строки в данных, которые содержат по крайней мере одно отсутствующее значение (NaN). Однако simsmooth использует Байесово увеличение данных, чтобы приписать непреддемонстрационные отсутствующие значения во время следующей оценки.

Рассмотрите 3-D модель VAR (4) для инфляции США (INFL), безработица (UNRATE), и федеральные фонды (FEDFUNDS) уровни.

$[\begin{array}{llllllllllllllllllll} {INFL}_{t} \\ {UNRATE}_{t} \\ {FEDFUNDS}_{t} \end{array}] = c + \sum_{j = 1}^{4} Φ_{j} [\begin{array}{llllllllllllllllllll} {INFL}_{t - j} \\ {UNRATE}_{t - j} \\ {FEDFUNDS}_{t - j} \end{array}] + [\begin{array}{cccccccccccccccccccc} ε_{1, t} \\ ε_{2, t} \\ ε_{3, t} \end{array}] .$

\forall $t$ , $ε_{t}$ серия независимых 3-D нормальных инноваций со средним значением 0 и ковариация $Σ$ . Примите слабое сопряженное предшествующее распределение для параметров $({[Φ_{1}, . . ., Φ_{4}, c]}^{'}, Σ)$ .

Загрузите и предварительно обработайте данные

Загрузите США макроэкономический набор данных. Вычислите уровень инфляции и стабилизируйте показатели безработицы и ставки по федеральным фондам.

load Data_USEconModel
seriesnames = ["INFL" "UNRATE" "FEDFUNDS"];
DataTable.INFL = 100*[NaN; price2ret(DataTable.CPIAUCSL)];
DataTable.DUNRATE = [NaN; diff(DataTable.UNRATE)];
DataTable.DFEDFUNDS = [NaN; diff(DataTable.FEDFUNDS)];
seriesnames(2:3) = "D" + seriesnames(2:3);

Несколько рядов имеют ведущий NaN значения, потому что их измерения не были доступны в то же время, что и другие измерения. Поскольку продвижение NaN значения могут вмешаться в преддемонстрационную спецификацию, удалить все строки, содержащие по крайней мере одно ведущее отсутствующее значение.

rmldDataTable = rmmissing(DataTable(:,seriesnames));

Создайте предшествующую модель

Создайте слабую сопряженную предшествующую модель путем определения большого коэффициента предшествующие отклонения. Задайте серийные имена ответа.

numseries = numel(seriesnames);
numlags = 4;

PriorMdl = conjugatebvarm(numseries,numlags,'SeriesNames',seriesnames);
numcoeffseqn = size(PriorMdl.V,1);
PriorMdl.V = 1e4*eye(numcoeffseqn);

Случайным образом поместите отсутствующие значения в данные

Чтобы проиллюстрировать симуляцию в присутствии отсутствующих значений, случайным образом поместите отсутствующие значения в данные после преддемонстрационного периода.

rng(1)                          % For reproducibility
T = size(rmldDataTable,1);
idxpre = 1:PriorMdl.P;          % Presample period
idxest = (PriorMdl.P + 1):T;    % Estimation period 

nmissing = 20;                  % Simulate at most nmissing missing values
sidx = [randsample(idxest,nmissing,true); randsample(1:numseries,nmissing,true)];
lsidx = sub2ind([T,numseries],sidx(1,:),sidx(2,:));
MissData = table2array(rmldDataTable);
MissData(lsidx) = NaN;
MissDataTable = rmldDataTable;
MissDataTable{:,:} = MissData;

Симулируйте параметры от следующего

Чертите 1 000 наборов параметров от апостериорного распределения путем вызова simsmooth, который оценивает апостериорное распределение параметров, и затем формирует следующее прогнозирующее распределение.

[Coeff,Sigma] = simsmooth(PriorMdl,MissDataTable.Variables);

Coeff 39 1000 матрица случайным образом чертивших векторов коэффициентов от следующего. Sigma 3 3 1 000 массивов случайным образом чертивших инновационных ковариационных матриц.

По умолчанию, simsmooth инициализирует модель VAR при помощи первых четырех наблюдений в данных.

Сопоставлять строки Coeff к коэффициентам получите сводные данные предшествующего распределения при помощи summarize. В таблице отобразите первый набор случайным образом чертивших коэффициентов с соответствующими именами.

Summary = summarize(PriorMdl,'off');
table(Coeff(:,1),'RowNames',Summary.CoeffMap)

ans=39×1 table
                      Var1   
                   __________

    AR{1}(1,1)        0.22109
    AR{1}(1,2)       -0.24034
    AR{1}(1,3)       0.093315
    AR{2}(1,1)        0.18329
    AR{2}(1,2)       -0.23178
    AR{2}(1,3)      -0.026301
    AR{3}(1,1)        0.39991
    AR{3}(1,2)        0.41141
    AR{3}(1,3)       0.054702
    AR{4}(1,1)       0.024944
    AR{4}(1,2)       -0.37372
    AR{4}(1,3)     -0.0095642
    Constant(1)       0.21499
    AR{1}(2,1)      -0.073776
    AR{1}(2,2)        0.36086
    AR{1}(2,3)       0.071088
      ⋮

В качестве альтернативы можно создать эмпирическую модель из ничьих и использовать summarize отобразить модель путем определения любого параметра отображения.

Отобразите сводные данные следующих ничьих как уравнение.

EmpMdl = empiricalbvarm(numseries,numlags,'SeriesNames',seriesnames,...
    'CoeffDraws',Coeff,'SigmaDraws',Sigma);
summarize(EmpMdl,'equation')

                                                                                 VAR Equations                                                                                
           | INFL(-1)  DUNRATE(-1)  DFEDFUNDS(-1)  INFL(-2)  DUNRATE(-2)  DFEDFUNDS(-2)  INFL(-3)  DUNRATE(-3)  DFEDFUNDS(-3)  INFL(-4)  DUNRATE(-4)  DFEDFUNDS(-4)  Constant 
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
 INFL      |  0.1447     -0.3685        0.1013      0.2974     -0.0959        0.0360      0.4115      0.2244        0.0474      0.0265     -0.2321        0.0030      0.1095  
           | (0.0744)    (0.1314)      (0.0370)    (0.0833)    (0.1509)      (0.0398)    (0.0833)    (0.1440)      (0.0403)    (0.0879)    (0.1301)      (0.0370)    (0.0744) 
 DUNRATE   | -0.0187      0.4445        0.0314      0.0836      0.2372        0.0489     -0.0407     -0.0548       -0.0064      0.0483     -0.1753        0.0027     -0.0597  
           | (0.0447)    (0.0808)      (0.0234)    (0.0514)    (0.0863)      (0.0230)    (0.0507)    (0.0906)      (0.0243)    (0.0514)    (0.0779)      (0.0225)    (0.0466) 
 DFEDFUNDS | -0.2046     -1.1927       -0.2524      0.2864     -0.2282       -0.2657      0.2709     -0.6231        0.0289     -0.0404      0.1043       -0.1236     -0.2952  
           | (0.1530)    (0.2931)      (0.0816)    (0.1832)    (0.3123)      (0.0857)    (0.1736)    (0.3105)      (0.0900)    (0.1866)    (0.2880)      (0.0758)    (0.1684) 
 
       Innovations Covariance Matrix       
           |   INFL     DUNRATE  DFEDFUNDS 
-------------------------------------------
 INFL      |  0.2842   -0.0098     0.1346  
           | (0.0286)  (0.0122)   (0.0464) 
 DUNRATE   | -0.0098    0.1062    -0.1496  
           | (0.0122)  (0.0106)   (0.0296) 
 DFEDFUNDS |  0.1346   -0.1496     1.3187  
           | (0.0464)  (0.0296)   (0.1422)

Смотрите увеличенные данные

Скрипт Open Live Script

Полагайте, что 3-D модель VAR (4) Симулирует Параметры от Апостериорного распределения при наличии Отсутствующих значений.

load Data_USEconModel
seriesnames = ["INFL" "UNRATE" "FEDFUNDS"];
DataTable.INFL = 100*[NaN; price2ret(DataTable.CPIAUCSL)];
DataTable.DUNRATE = [NaN; diff(DataTable.UNRATE)];
DataTable.DFEDFUNDS = [NaN; diff(DataTable.FEDFUNDS)];
seriesnames(2:3) = "D" + seriesnames(2:3);

Удалите все строки, которые содержат ведущие отсутствующие значения.

rmldDataTable = rmmissing(DataTable(:,seriesnames));

Создайте слабую сопряженную предшествующую модель. Задайте серийные имена ответа.

numseries = numel(seriesnames);
numlags = 4;

PriorMdl = conjugatebvarm(numseries,numlags,'SeriesNames',seriesnames);
numcoeffseqn = size(PriorMdl.V,1);
PriorMdl.V = 1e4*eye(numcoeffseqn);

Случайным образом поместите отсутствующие значения в данные после преддемонстрационного периода.

rng(1)                          % For reproducibility
T = size(rmldDataTable,1);
idxpre = 1:PriorMdl.P;          % Presample period
idxest = (PriorMdl.P + 1):T;    % Estimation period 

nmissing = 20;                  % Simulate at most nmissing missing values
sidx = [randsample(idxest,nmissing,true); randsample(1:numseries,nmissing,true)];
lsidx = sub2ind([T,numseries],sidx(1,:),sidx(2,:));
MissData = table2array(rmldDataTable);
MissData(lsidx) = NaN;
MissDataTable = rmldDataTable;
MissDataTable{:,:} = MissData;

Чертите 1 000 наборов параметров от апостериорного распределения путем вызова simsmooth. Возвратите значения, которые более сглаженная симуляция приписывает для недостающих наблюдений.

[~,~,NaNDraws] = simsmooth(PriorMdl,MissDataTable.Variables);

NaNDraws 19 1000 матрица случайным образом чертивших векторов отклика от следующего прогнозирующего распределения. Элементы соответствуют отсутствующим значениям в данных, упорядоченных постолбцовым поиском. Например, NaNDraws(3,1) первый случайным образом чертивший оценочный ответ третьего отсутствующего значения в данных. Найдите соответствующее значение в данных.

[idxi,idxj] = find(ismissing(MissDataTable),3);
responsename = seriesnames(idxj(end))

responsename = 
"INFL"

observationtime = MissDataTable.Time(idxi(end))

observationtime = datetime
   Q3-65

Постройте эмпирическое распределение оценочных значений уровня инфляции во время Q3-65.

histogram(NaNDraws(3,:))
title('Q3-65 Inflation Rate Empirical Distribution')

Figure contains an axes object. The axes object with title Q3-65 Inflation Rate Empirical Distribution contains an object of type histogram.

Настройте опции выборки более сглаженной симуляции

Скрипт Open Live Script

Загрузите США макроэкономический набор данных. Вычислите уровень инфляции, стабилизируйте показатели безработицы и ставки по федеральным фондам, и удалите отсутствующие значения (данные включают только ведущие отсутствующие значения).

load Data_USEconModel
seriesnames = ["INFL" "UNRATE" "FEDFUNDS"];
DataTable.INFL = 100*[NaN; price2ret(DataTable.CPIAUCSL)];
DataTable.DUNRATE = [NaN; diff(DataTable.UNRATE)];
DataTable.DFEDFUNDS = [NaN; diff(DataTable.FEDFUNDS)];
seriesnames(2:3) = "D" + seriesnames(2:3);
rmDataTable = rmmissing(DataTable);

Создайте слабую сопряженную предшествующую модель. Задайте серийные имена ответа.

numseries = numel(seriesnames);
numlags = 4;

PriorMdl = conjugatebvarm(numseries,numlags,'SeriesNames',seriesnames);
numcoeffseqn = size(PriorMdl.V,1);
PriorMdl.V = 1e4*eye(numcoeffseqn);

Симулируйте 5 000 коэффициентов и инновационных ковариационных матриц от апостериорного распределения. Задайте электротермотренировку 1 000 и утончающийся фактор 5.

rng(1); % For reproducibility
[Coeff,Sigma] = simsmooth(PriorMdl,rmDataTable{:,seriesnames},...
    'NumDraws',5000,'BurnIn',1000,'Thin',5);

Coeff 39 5000 матрица коэффициентов и Sigma 3 3 5 000 массивов инновационных ковариационных матриц. Оба Coeff и Sigma случайным образом чертятся от апостериорного распределения.

Задайте содействующие начальные значения для более сглаженной симуляции

Скрипт Open Live Script

Полагайте, что 3-D модель VAR (4) Симулирует Параметры от Апостериорного распределения при наличии Отсутствующих значений. В этом случае примите, что предшествующая модель полусопряжена.

load Data_USEconModel
seriesnames = ["INFL" "UNRATE" "FEDFUNDS"];
DataTable.INFL = 100*[NaN; price2ret(DataTable.CPIAUCSL)];
DataTable.DUNRATE = [NaN; diff(DataTable.UNRATE)];
DataTable.DFEDFUNDS = [NaN; diff(DataTable.FEDFUNDS)];
seriesnames(2:3) = "D" + seriesnames(2:3);
rmDataTable = rmmissing(DataTable);

Создайте полусопряженную предшествующую модель. Задайте серийные имена ответа.

numseries = numel(seriesnames);
numlags = 4;

PriorMdl = bayesvarm(numseries,numlags,'ModelType','semiconjugate',...
    'SeriesNames',seriesnames);

Чтобы получить начальные значения для коэффициентов, считайте коэффициенты из модели VAR адаптированными к первым 30 наблюдениям.

Задайте наборы индекса тот раздел данные в четыре набора:

Длина p = 4 периода инициализации для динамического компонента модели
$n_{0}$ = 30 наблюдений, чтобы оценить VAR для содействующих начальных значений
Длина p = 4 периода инициализации для динамического компонента модели Bayesian VAR
Оставление $n_{1}$ наблюдения, чтобы оценить следующее

T = size(rmDataTable);
n0 = 30;
idxpre0 = 1:PriorMdl.P;
idxest0 = (idxpre0(end) + 1):(idxpre0(end) + 1 + n0);
idxpre1 = (idxest0(end) + 1 - PriorMdl.P):idxest0(end);
idxest1 = (idxest0(end) + 1):T;
n1 = numel(idxest1);

Получите начальные содействующие значения, подбирая модель VAR к первым 34 наблюдениям. Используйте первые четыре наблюдения в качестве предварительной выборки.

Mdl0 = varm(PriorMdl.NumSeries,PriorMdl.P);
EstMdl0 = estimate(Mdl0,rmDataTable{idxest0,seriesnames},'Y0',rmDataTable{idxpre0,seriesnames});

estimate возвращает объект модели, содержащий содействующие оценки AR в матричной форме и константы в векторе. Байесовы функции VAR требуют начальных содействующих значений в векторе. Отформатируйте начальные содействующие значения.

Coeff0 = [EstMdl0.AR{:} EstMdl0.Constant].';
Coeff0 = Coeff0(:);

Симулируйте 1 000 коэффициентов и инновационных ковариационных матриц от апостериорного распределения. Задайте остающиеся наблюдения, от которых можно оценить следующее. Инициализируйте модель VAR путем определения последних четырех наблюдений в предыдущей выборке оценки как предварительная выборка и задайте начальный вектор коэффициентов, чтобы инициализировать следующую выборку.

rng(1); % For reproducibility
[Coeff,Sigma] = simsmooth(PriorMdl,rmDataTable{idxest1,seriesnames},...
    'Y0',rmDataTable{idxpre1,seriesnames},'Coeff0',Coeff0);

Coeff 39 1000 матрица коэффициентов и Sigma 3 3 1 000 массивов инновационных ковариационных матриц. Оба Coeff и Sigma случайным образом чертятся от апостериорного распределения.

Предскажите ответы от следующего прогнозирующего распределения

Скрипт Open Live Script

Загрузите и предварительно обработайте данные

load Data_USEconModel
seriesnames = ["INFL" "UNRATE" "FEDFUNDS"];
DataTable.INFL = 100*[NaN; price2ret(DataTable.CPIAUCSL)];
DataTable.DUNRATE = [NaN; diff(DataTable.UNRATE)];
DataTable.DFEDFUNDS = [NaN; diff(DataTable.FEDFUNDS)];
seriesnames(2:3) = "D" + seriesnames(2:3);
rmDataTable = rmmissing(DataTable);

Создайте предшествующую модель

Создайте слабую сопряженную предшествующую модель. Задайте серийные имена ответа.

numseries = numel(seriesnames);
numlags = 4;

PriorMdl = conjugatebvarm(numseries,numlags,'SeriesNames',seriesnames);
numcoeffseqn = size(PriorMdl.V,1);
PriorMdl.V = 1e4*eye(numcoeffseqn);

Предскажите ответы Используя forecast

Непосредственно предскажите два года (восемь четвертей) наблюдений от следующего прогнозирующего распределения. forecast оценивает апостериорное распределение параметров, и затем формирует следующее прогнозирующее распределение.

rng(1); % For reproducibility
numperiods = 8;
YF = forecast(PriorMdl,numperiods,rmDataTable{:,seriesnames});

YF 8 3 матрица предсказанных ответов.

Постройте предсказанные ответы.

fh = rmDataTable.Time(end) + calquarters(1:8);
for j = 1:PriorMdl.NumSeries
    subplot(3,1,j)
    plot(rmDataTable.Time(end - 20:end),rmDataTable{end - 20:end,seriesnames(j)},'r',...
        [rmDataTable.Time(end) fh],[rmDataTable{end,seriesnames(j)}; YF(:,j)],'b');
    legend("Observed","Forecasted",'Location','NorthWest')
    title(seriesnames(j))
end

Figure contains 3 axes objects. Axes object 1 with title INFL contains 2 objects of type line. These objects represent Observed, Forecasted. Axes object 2 with title DUNRATE contains 2 objects of type line. These objects represent Observed, Forecasted. Axes object 3 with title DFEDFUNDS contains 2 objects of type line. These objects represent Observed, Forecasted.

Предскажите ответы Используя simsmooth

Сконфигурируйте набор данных для получения прогнозов от simsmooth путем конкатенации numperiods- numseries расписание отсутствующих значений в конец набора.

fTT = array2timetable(NaN(numperiods,numseries),'RowTimes',fh,...
    'VariableNames',seriesnames);
frmDataTable = [rmDataTable(:,seriesnames); fTT];
tail(frmDataTable)

ans=8×3 timetable
    Time     INFL    DUNRATE    DFEDFUNDS
    _____    ____    _______    _________

    Q2-09    NaN       NaN         NaN   
    Q3-09    NaN       NaN         NaN   
    Q4-09    NaN       NaN         NaN   
    Q1-10    NaN       NaN         NaN   
    Q2-10    NaN       NaN         NaN   
    Q3-10    NaN       NaN         NaN   
    Q4-10    NaN       NaN         NaN   
    Q1-11    NaN       NaN         NaN

Предскажите модель VAR с помощью simsmooth. Как forecast, simsmooth оценивает апостериорное распределение, таким образом, оно требует предшествующей модели и данных. Задайте данные, содержащие запаздывающий NaNs.

[~,~,~,YMean] = simsmooth(PriorMdl,frmDataTable.Variables);

YMean почти равно frmDataTable, за этими исключениями:

YMean исключает строки, соответствующие преддемонстрационному периоду frmDataTable(1:4,:).
Если frmDataTable(j,k) isnan, YMean(j,k) среднее значение следующего прогнозирующего распределения ответа k во время j.

Создайте расписание из YMean.

YMeanTT = array2timetable(YMean,'RowTimes',frmDataTable.Time((PriorMdl.P + 1):end),...
    'VariableNames',seriesnames);

Постройте предсказанные ответы.

for j = 1:PriorMdl.NumSeries
    subplot(3,1,j)
    plot(YMeanTT.Time((end - 20 - numperiods):(end - numperiods)),YMeanTT{(end - 20 - numperiods):(end - numperiods),j},'r',...
        YMeanTT.Time((end - numperiods):end),YMeanTT{(end - numperiods):end,j},'b');
        legend("Observed","Forecasted",'Location','NorthWest')
    title(seriesnames(j))
end

Оцените условные прогнозы

Скрипт Open Live Script

load Data_USEconModel
seriesnames = ["INFL" "UNRATE" "FEDFUNDS"];
DataTable.INFL = 100*[NaN; price2ret(DataTable.CPIAUCSL)];
DataTable.DUNRATE = [NaN; diff(DataTable.UNRATE)];
DataTable.DFEDFUNDS = [NaN; diff(DataTable.FEDFUNDS)];
seriesnames(2:3) = "D" + seriesnames(2:3);
rmDataTable = rmmissing(DataTable);

Создайте слабую сопряженную предшествующую модель. Задайте серийные имена ответа.

numseries = numel(seriesnames);
numlags = 4;

PriorMdl = conjugatebvarm(numseries,numlags,'SeriesNames',seriesnames);
numcoeffseqn = size(PriorMdl.V,1);
PriorMdl.V = 1e4*eye(numcoeffseqn);

Условное прогнозирование происходит, когда значения отклика известны или выдвинули гипотезу в горизонте прогноза, и неизвестные значения предсказаны обусловленные на известных значениях. Предположим что изменение уровня безработицы (DUNRATE) остается на уровне одного процентного пункта через горизонт прогноза 2D года.

Сконфигурируйте набор данных для получения прогнозов от simsmooth путем конкатенации numperiods- numseries расписание отсутствующих значений в конец набора. Для изменения уровня безработицы замените отсутствующие значения на вектор из единиц.

rng(1); % For reproducibility
numperiods = 8;
fh = rmDataTable.Time(end) + calquarters(1:8);

fTT = array2timetable(NaN(numperiods,numseries),'RowTimes',fh,...
    'VariableNames',seriesnames);

frmDataTable = [rmDataTable(:,seriesnames); fTT];
frmDataTable.DUNRATE((end - numperiods + 1):end) = ones(numperiods,1);
tail(frmDataTable)

ans=8×3 timetable
    Time     INFL    DUNRATE    DFEDFUNDS
    _____    ____    _______    _________

    Q2-09    NaN        1          NaN   
    Q3-09    NaN        1          NaN   
    Q4-09    NaN        1          NaN   
    Q1-10    NaN        1          NaN   
    Q2-10    NaN        1          NaN   
    Q3-10    NaN        1          NaN   
    Q4-10    NaN        1          NaN   
    Q1-11    NaN        1          NaN

Получите прогнозы для уровня инфляции и ряда изменения ставки по федеральным фондам, учитывая, что изменение уровня безработицы один для целого горизонта.

[~,~,~,YMean] = simsmooth(PriorMdl,frmDataTable.Variables);

YMean почти равно frmDataTable, за этими исключениями:

YMean исключает строки, соответствующие преддемонстрационному периоду frmDataTable(1:4,:).
Если frmDataTable(j,k) isnan, YMean(j,k) среднее значение следующего прогнозирующего распределения ответа k во время j.

Создайте расписание из YMean.

YMeanTT = array2timetable(YMean,'RowTimes',frmDataTable.Time((PriorMdl.P + 1):end),...
    'VariableNames',seriesnames);

Постройте предсказанные ответы.

for j = 1:PriorMdl.NumSeries
    subplot(3,1,j)
    plot(YMeanTT.Time((end - 20 - numperiods):(end - numperiods)),YMeanTT{(end - 20 - numperiods):(end - numperiods),j},'r',...
        YMeanTT.Time((end - numperiods):end),YMeanTT{(end - numperiods):end,j},'b');
        legend("Observed","Forecasted",'Location','NorthWest')
    title(seriesnames(j))
end

Предскажите модель VARX

Скрипт Open Live Script

Считайте 2D модель VARX(1) для США действительным GDP (RGDP) и инвестиции (GCE) уровни, который обрабатывает персональное потребление (PCEC) уровень как внешний:

$[\begin{array}{llllllllllllllllllll} {RGDP}_{t} \\ {GCE}_{t} \end{array}] = c + Φ [\begin{array}{llllllllllllllllllll} {RGDP}_{t - 1} \\ {GCE}_{t - 1} \end{array}] + {PCEC}_{t} β + ε_{t} .$

\forall $t$ , $ε_{t}$ серия независимых 2D нормальных инноваций со средним значением 0 и ковариация $Σ$ . Примите следующие предшествующие распределения:

${[\begin{array}{c} Φ & c & β \end{array}]}^{'} | Σ \sim Ν_{4 \times 2} (Μ, V, Σ)$ , где M 4 2 матрица средних значений и $V$ матрица шкалы среди коэффициента 4 на 4. Эквивалентно, $vec ({[\begin{array}{c} Φ & c & β \end{array}]}^{'}) | Σ \sim Ν_{8} (vec (Μ), Σ \otimes V)$ .
$Σ \sim I n v e r s e W i s h a r t (Ω, ν),$ где Ω является матрицей шкалы 2 на 2 и $ν$ степени свободы.

Загрузите США макроэкономический набор данных. Вычислите действительный GDP, инвестиции и персональный ряд нормы потребления. Удалите все отсутствующие значения из получившегося ряда.

load Data_USEconModel
DataTable.RGDP = DataTable.GDP./DataTable.GDPDEF;
seriesnames = ["PCEC"; "RGDP"; "GCE"];
rates = varfun(@price2ret,DataTable,'InputVariables',seriesnames);
rates = rmmissing(rates);
rates.Properties.VariableNames = seriesnames;

Создайте сопряженную предшествующую модель для 2D VARX (1) параметры модели.

numseries = 2;
numlags = 1;
numpredictors = 1;
PriorMdl = conjugatebvarm(numseries,numlags,'NumPredictors',numpredictors,...
    'SeriesNames',seriesnames(2:end));

Создайте наборы индекса тот раздел данные в выборки прогноза и оценку. Задайте горизонт прогноза двух лет.

T = size(rates,1);
numperiods = 8;
idxest = 1:(T - numperiods); % Includes presample
idxf = (T - numperiods + 1):T;
idxtot = [idxest idxf];

Симуляция более сглаженные прогнозы путем приписывания отсутствующих значений. Поэтому создайте набор данных, который содержит отсутствующие значения для ответов в горизонте прогноза.

missingrates = rates;
missingrates{idxf,PriorMdl.SeriesNames} = nan(numperiods,PriorMdl.NumSeries);

Предскажите ответы в горизонте прогноза. Задайте преддемонстрационные наблюдения и внешние данные о предикторе. Возвратите стандартные отклонения следующего прогнозирующего распределения.

rng(1) % For reproducibility
[~,~,~,YMean,YStd] = simsmooth(PriorMdl,missingrates{:,PriorMdl.SeriesNames},...
    'X',missingrates{:,seriesnames(1)});

Создайте расписание из YMean.

YMeanTT = array2timetable(YMean,'RowTimes',rates.Time((PriorMdl.P + 1):end),...
    'VariableNames',PriorMdl.SeriesNames);

Постройте предсказанные ответы.

for j = 1:PriorMdl.NumSeries
    subplot(PriorMdl.NumSeries,1,j)
    plot(rates.Time((end - 20):end),rates{(end - 20):end,PriorMdl.SeriesNames(j)},'r',...
        YMeanTT.Time((end - numperiods):end),YMeanTT{(end - numperiods):end,PriorMdl.SeriesNames(j)},'b');
        legend("Observed","Forecasted",'Location','NorthWest')
    title(PriorMdl.SeriesNames(j))
end

Figure contains 2 axes objects. Axes object 1 with title RGDP contains 2 objects of type line. These objects represent Observed, Forecasted. Axes object 2 with title GCE contains 2 objects of type line. These objects represent Observed, Forecasted.

Входные параметры

свернуть все

`PriorMdl` — Предшествующая модель Bayesian VAR
`conjugatebvarm` объект модели | `semiconjugatebvarm` объект модели | `diffusebvarm` объект модели | `normalbvarm` объект модели

Предшествующая модель Bayesian VAR в виде объекта модели в этой таблице.

Объект модели	Описание
`conjugatebvarm`	Зависимый, матричная нормальная инверсия Уишарт спрягают модель, возвращенную `bayesvarm`, `conjugatebvarm`, или `estimate`
`semiconjugatebvarm`	Независимый, нормальный обратный Уишарт полуспрягает предшествующую модель, возвращенную `bayesvarm` или `semiconjugatebvarm`
`diffusebvarm`	Рассейте предшествующую модель, возвращенную `bayesvarm` или `diffusebvarm`
`normalbvarm`	Нормальная сопряженная модель с фиксированной инновационной ковариационной матрицей, возвращенной `bayesvarm`, `normalbvarm`, или `estimate`

`Y` — Наблюдаемый многомерный ряд ответа
числовая матрица

Наблюдаемый многомерный ряд ответа, к который simsmooth подбирает модель в виде numobs- numseries числовая матрица.

numobs объем выборки. numseries количество переменных отклика (PriorMdl.NumSeries).

Строки соответствуют наблюдениям, и последняя строка содержит последнее наблюдение. Столбцы соответствуют отдельным переменным отклика.

NaN значения в Y укажите на недостающие наблюдения. simsmooth непреддемонстрационные отсутствующие значения замен с обвинением (см. NaNDraws) как часть процесса выборки.

Y представляет продолжение преддемонстрационной серии Y0 ответа.

Совет

Получить numperiods прогнозы из выборки, конкатенируйте numperiods- numseries матрица NaNs в конец Y. simsmooth возвращает прогнозы и стандартные отклонения в соответствующих элементах YMean и YStd, соответственно. Например:
```
numperiods = 8;
Y = [Y; NaN(numperiods,PriorMdl.NumSeries)];
```
Чтобы получить прогнозы, обусловленные на наблюдаемом (или выдвинул гипотезу) значения в горизонте прогноза, конкатенируйте numperiods- numseries матрица NaNs и наблюдаемый или выдвинул гипотезу значения в конец Y. Например, в 2D системе, получите прогноз "один шаг вперед" переменной отклика 1, учитывая, что переменная отклика 2 0.5 путем определения
```
Y = [Y; [NaN 0.5]];
```

Типы данных: double

Аргументы name-value

Задайте дополнительные разделенные запятой пары Name,Value аргументы. Name имя аргумента и Value соответствующее значение. Name должен появиться в кавычках. Вы можете задать несколько аргументов в виде пар имен и значений в любом порядке, например: Name1, Value1, ..., NameN, ValueN.

Пример: 'Y0',Y0,'X',X задает преддемонстрационные данные об ответе Y0 инициализировать модель VAR для следующей симуляции и данные о предикторе X для внешнего компонента регрессии.

`Y0` — Преддемонстрационные данные об ответе
числовая матрица

Преддемонстрационные данные об ответе, чтобы инициализировать модель VAR для симуляции в виде разделенной запятой пары, состоящей из 'Y0' и numpreobs- numseries числовая матрица. numpreobs количество преддемонстрационных наблюдений.

Строки соответствуют преддемонстрационным наблюдениям, и последняя строка содержит последнее наблюдение. Y0 должен иметь, по крайней мере, PriorMdl.P 'Строки' . Если вы предоставляете больше строк, чем необходимый, simsmooth использует последний PriorMdl.P наблюдения только.

Столбцы должны соответствовать ряду ответа в Y.

По умолчанию, simsmooth использование Y(1:PriorMdl.P,:) как преддемонстрационные наблюдения, и затем оценивает следующее использование Y((PriorMdl.P + 1):end,:). Это действие уменьшает эффективный объем выборки. Количество строк выходных параметров YMean и YStd size(Y,1) – PriorMdl.P. Если Y0 содержит по крайней мере один NaN, simsmooth выдает ошибку.

Типы данных: double

`X` — Данные о предикторе
числовая матрица

Данные о предикторе для внешнего компонента регрессии в модели в виде разделенной запятой пары, состоящей из 'X' и numobs- PriorMdl.NumPredictors числовая матрица.

Строки соответствуют наблюдениям, и последняя строка содержит последнее наблюдение. simsmooth не использует компонент регрессии в преддемонстрационный период. X должен иметь, по крайней мере, столько наблюдений, сколько наблюдения использовали после преддемонстрационного периода.

Если вы задаете Y0, затем X должен иметь, по крайней мере, numobs строки (см. Y).
В противном случае, X должен иметь, по крайней мере, numobs – PriorMdl.P наблюдения с учетом преддемонстрационного удаления.

В любом случае, если вы предоставляете больше строк, чем необходимый, simsmooth использует последние наблюдения только.

Столбцы соответствуют отдельным переменным предикторам. Все переменные предикторы присутствуют в компоненте регрессии каждого уравнения ответа.

Если X содержит по крайней мере один NaN, simsmooth выдает ошибку.

Типы данных: double

`NumDraws` — Количество случайных ничьих
1 (значение по умолчанию) | положительное целое число

Количество случайных ничьих от распределений в виде разделенной запятой пары, состоящей из 'NumDraws' и положительное целое число.

Пример: 'NumDraws',1e7

Типы данных: double

`BurnIn` — Количество ничьих, чтобы удалить с начала выборки
0 (значение по умолчанию) | неотрицательный скаляр

Количество ничьих, чтобы удалить с начала выборки уменьшать переходные эффекты в виде разделенной запятой пары, состоящей из 'BurnIn' и неотрицательный скаляр. Для получения дополнительной информации, на как simsmooth уменьшает полную выборку, см. Алгоритмы.

Совет

Помочь вам задать соответствующий размер электротермотренировки:

Определите степень переходного поведения в выборке путем определения 'BurnIn',0.
Симулируйте несколько тысяч наблюдений при помощи simsmooth.
Постройте графики трассировки.

Пример: 'BurnIn',0

Типы данных: double

`Thin` — Настроенный множитель объема выборки
1 (значение по умолчанию) | положительное целое число

Настроенный множитель объема выборки в виде разделенной запятой пары, состоящей из 'Thin' и положительное целое число.

Фактическим объемом выборки является BurnIn + NumDraws*Thin. После отбрасывания выжигания дефектов, simsmooth отбрасывает каждый Thin– 1 чертит, и затем сохраняет следующую ничью. Для получения дополнительной информации о как simsmooth уменьшает полную выборку, см. Алгоритмы.

Совет

Уменьшать потенциальную большую последовательную корреляцию в выборке или уменьшать потребление памяти ничьих, сохраненных в PriorMdl, задайте большое значение для Thin.

Пример: 'Thin',5

Типы данных: double

`Coeff0` — Начальное значение коэффициентов модели VAR для сэмплера Гиббса
числовой вектор-столбец

Начальное значение коэффициентов модели VAR для сэмплера Гиббса в виде разделенной запятой пары, состоящей из 'Coeff0' и числовой вектор-столбец с (Mdl. NumSeries*k)-by-NumDraws элементы, где k = Mdl.NumSeries*Mdl.P + Mdl.IncludeIntercept + Mdl.IncludeTrend + Mdl.NumPredictors, который является количеством коэффициентов в уравнении ответа. Для получения дополнительной информации на структуре Coeff0, смотрите выход CoeffDraws.

По умолчанию, Coeff0 многомерная оценка наименьших квадратов.

Совет

Задавать Coeff0:
1. Установите отдельные переменные для начальных значений каждой матрицы коэффициентов и вектора.
2. Горизонтально конкатенируйте все содействующие средние значения в этом порядке:
  
  $C o e f f = [\begin{matrix} Φ_{1} & Φ_{2} & \dots & Φ_{p} & c & δ & Β \end{matrix}] .$
3. Векторизуйте транспонирование содействующей средней матрицы.
  Coeff0 = Coeff.'; Coeff0 = Coeff0(:);
Хорошая практика должна запуститься simsmooth многократно с различными начальными значениями параметра. Проверьте, что оценки от каждого запуска сходятся к подобным значениям.

Типы данных: double

`Sigma0` — Начальное значение инновационной ковариационной матрицы для сэмплера Гиббса
положительная определенная числовая матрица

Начальное значение инновационной ковариационной матрицы для сэмплера Гиббса в виде разделенной запятой пары, состоящей из 'Sigma0' и PriorMdl.NumSeries- PriorMdl.NumSeries положительная определенная числовая матрица. По умолчанию, Sigma0 остаточная среднеквадратическая ошибка от многомерных наименьших квадратов. Строки и столбцы соответствуют инновациям в уравнениях переменных отклика, упорядоченных Mdl.SeriesNames.

Совет

Хорошая практика должна запуститься simsmooth многократно с различными начальными значениями параметра. Проверьте, что оценки от каждого запуска сходятся к подобным значениям.

Типы данных: double

Выходные аргументы

свернуть все

`CoeffDraws` — Симулированные коэффициенты модели VAR
числовая матрица

Симулированные коэффициенты модели VAR, возвращенные как (PriorMdl. NumSeries*k)-by-NumDraws числовая матрица, где k = PriorMdl.NumSeries*PriorMdl.P + PriorMdl.IncludeIntercept + PriorMdl.IncludeTrend + PriorMdl.NumPredictors, который является количеством коэффициентов в уравнении ответа.

Каждый столбец является последовательной ничьей (вектор из коэффициентов) от апостериорного распределения.

Для ничьей j, CoeffDraws (1:kJ) соответствует всем коэффициентам в уравнении переменной отклика PriorMdl.SeriesNames(1), Коэффициент ((k + 1): (2*kJ) соответствует всем коэффициентам в уравнении переменной отклика PriorMdl.SeriesNames(2), и так далее. Для набора индексов, соответствующих уравнению:

Элементы 1 через PriorMdl.NumSeries соответствуйте задержке 1 коэффициент AR переменных отклика, упорядоченных PriorMdl.SeriesNames.
Элементы PriorMdl.NumSeries + 1 через 2*PriorMdl.NumSeries соответствуйте задержке 2 коэффициента AR переменных отклика, упорядоченных PriorMdl.SeriesNames.
В общем случае элементы (q – 1) *PriorMdl.NumSeries + 1 через q*PriorMdl.NumSeries соответствуйте задержке q Коэффициенты AR переменных отклика упорядочены PriorMdl.SeriesNames.
Если PriorMdl.IncludeConstant true, элемент PriorMdl.NumSeries*PriorMdl.P + 1 константа модели.
Если Mdl.IncludeTrend true, элемент PriorMdl.NumSeries*PriorMdl.P + 2 линейный коэффициент тренда времени.
Если PriorMdl.NumPredictors > 0, элементы PriorMdl.NumSeries*PriorMdl.P + 3 через k составьте вектор из коэффициентов регрессии внешних переменных.

Этот рисунок показывает структуру CoeffDraws (: J) для 2D модели VAR (3), которая содержит постоянный вектор и четыре внешних предиктора.

$[\overset{y_{1, t}}{\overset{︷}{\begin{matrix} ϕ_{1, 11} & ϕ_{1, 12} & ϕ_{2, 11} & ϕ_{2, 12} & ϕ_{3, 11} & ϕ_{3, 12} & c_{1} & β_{11} & β_{12} & β_{13} & β_{14} \end{matrix}}} \overset{y_{2, t}}{\overset{︷}{\begin{matrix} ϕ_{1, 21} & ϕ_{1, 22} & ϕ_{2, 21} & ϕ_{2, 22} & ϕ_{3, 21} & ϕ_{3, 22} & c_{2} & β_{21} & β_{22} & β_{23} & β_{24} \end{matrix}}}],$

где

ϕ _{q, jk} является элементом (j, k) задержки матрица коэффициентов AR q.
c _j является константой модели в уравнении переменной отклика j.
B _{j u} является коэффициентом регрессии внешней переменной u в уравнении переменной отклика j.

`SigmaDraws` — Симулированные инновационные ковариационные матрицы
массив положительных определенных числовых матриц

Симулированные инновационные ковариационные матрицы, возвращенные как PriorMdl.NumSeries- PriorMdl.NumSeries- NumDraws массив положительных определенных числовых матриц.

Каждая страница является последовательной ничьей (ковариация) от апостериорного распределения. Строки и столбцы соответствуют инновациям в уравнениях переменных отклика, упорядоченных PriorMdl.SeriesNames.

Если PriorMdl normalbvarm объект, все ковариации в SigmaDraws равны PriorMdl.Covariance.

`NaNDraws` — Обвинения для недостающих данных об ответе
числовая матрица

Обвинения для недостающих данных об ответе, возвращенных как numNaNs- NumDraws числовая матрица, где numNaNs = sum(isNaN(Y)), количество NaNs в данных об ответе.

Каждый столбец является последовательной ничьей (вектор из обвинений ответа) от следующего прогнозирующего распределения.

Каждая строка соответствует NaN в Y. simsmooth определяет порядок строк при помощи постолбцового поиска. Например, предположите Y следующая матрица.

Y = [  1  NaN;...
      NaN  2 ;...
      NaN  5 ;...
        7  8];

Здесь, NaNDraws 3 NumDraws матрица. Для ничьей j, NaNDraws (1, j) содержит оценочное значение переменной отклика PriorMdl.SeriesNames(1) во время 2, NaNDraws (2, j) содержит оценочное значение переменной отклика PriorMdl.SeriesNames(1) во время 3, и NaNDraws (3, j) содержит оценочное значение переменной отклика PriorMdl.SeriesNames(2) во время 1.

`YMean` — Увеличенные данные об ответе
числовая матрица

Увеличенные данные об ответе, возвращенные как numobs- PriorMdl.NumSeries числовая матрица. YMean равно непреддемонстрационному фрагменту данных об ответе Y, но simsmooth замены каждый NaN с соответствующим средним значением следующего прогнозирующего распределения (YMean содержит нулевые отсутствующие значения).

`YStd` — Стандартные отклонения следующего прогнозирующего распределения
числовая матрица

Стандартные отклонения следующего прогнозирующего распределения оценочных ответов, возвращенных как numobs- PriorMdl.NumSeries числовая матрица. Размерности YStd и YMean соответствовать.

Отсутствующие значения в данных об ответе Y, которые соответствуют оценочным значениям в YMean, имейте ненулевое стандартное отклонение. Соответствие стандартных отклонений ненедостающим данным об ответе 0.

Больше о

свернуть все

Байесова векторная авторегрессия (VAR) модель

Bayesian VAR model обрабатывает все коэффициенты и инновационную ковариационную матрицу как случайные переменные в m - размерная, стационарная модель VARX(p). Модель имеет одну из трех форм, описанных в этой таблице.

Модель	Уравнение
VAR уменьшаемой формы (p) в обозначении разностного уравнения	$y_{t} = Φ_{1} y_{t - 1} + ... + Φ_{p} y_{t - p} + c + δ t + Β x_{t} + ε_{t} .$
Многомерная регрессия	$y_{t} = Z_{t} λ + ε_{t} .$
Матричная регрессия	$y_{t} = Λ^{'} z_{t}^{'} + ε_{t} .$

В течение каждого раза t = 1..., T:

_yt является m - размерный наблюдаемый вектор отклика, где m = numseries.
_Φ1, …, Φ_p является m-by-m содействующие матрицы AR задержек 1 через p, где p = numlags.
c является m-by-1 вектор из констант модели если IncludeConstant true.
δ является m-by-1 вектор из линейных коэффициентов тренда времени если IncludeTrend true.
Β m-by-r матрица коэффициентов регрессии r-by-1 вектор из наблюдаемых внешних предикторов x _t, где r = NumPredictors. Все переменные предикторы появляются в каждом уравнении.
$z_{t} = [\begin{matrix} y_{t - 1}^{'} & y_{t - 2}^{'} & \dots & y_{t - p}^{'} & 1 & t & x_{t}^{'} \end{matrix}],$ который является 1 на (mp + r + 2) вектор, и Z _t является m-by-m матрица диагонали блока (mp + r + 2)

$[\begin{matrix} z_{t} & 0_{z} & \dots & 0_{z} \\ 0_{z} & z_{t} & \dots & 0_{z} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ 0_{z} & 0_{z} & 0_{z} & z_{t} \end{matrix}],$
где 0_z является 1 на (mp + r + 2) нулевой вектор.
$Λ = {[\begin{matrix} Φ_{1} & Φ_{2} & \dots & Φ_{p} & c & δ & Β \end{matrix}]}^{'}$ , который является (mp + r + 2)-by-m случайная матрица коэффициентов и m (mp + r + 2)-by-1 векторный λ = vec (Λ).
_εt является m-by-1 вектор из случайных, последовательно некоррелированых, многомерных нормальных инноваций с нулевым вектором для среднего значения и m-by-m матрица Σ для ковариации. Это предположение подразумевает, что вероятность данных

$ℓ (Λ, Σ | y, x) = \prod_{t = 1}^{T} f (y_{t}; Λ, Σ, z_{t}),$
где f является m - размерная многомерная нормальная плотность со средним z _t Λ и ковариация Σ, оцененный в y _t.

Прежде, чем рассмотреть данные, вы налагаете предположение joint prior distribution на (Λ,Σ), которым управляет распределение π (Λ,Σ). В Байесовом анализе распределение параметров обновляется с информацией о параметрах, полученных из вероятности данных. Результатом является π joint posterior distribution (Λ,Σ | Y, X, Y ₀), где:

Y является T-by-m матрица, содержащая целый ряд ответа {y _t}, t = 1, …, T.
X является T-by-m матрица, содержащая целый внешний ряд {x _t}, t = 1, …, T.
Y ₀ является p-by-m, матрица преддемонстрационных данных раньше инициализировала модель VAR для оценки.

Следующее прогнозирующее распределение

posterior predictive distribution следующей модели Bayesian VAR (p) π (_Yf |Y, X) является распределением следующих переменных отклика будущего τ после итогового наблюдения в выборке оценки _Yf = [y _{T +1}, y _{T +2}, …, y _{T +τ}], учитывая следующее, маргинализованный по Λ и Σ:

Предварительная выборка и демонстрационные данные об ответе оценки Y
Коэффициенты Λ
Инновационная ковариационная матрица Σ
Оценка и будущие демонстрационные внешние данные X

Символически,

$π (Y_{f} | Y, X) = \int π (Y_{f} | Y, X, Λ, Σ) π (Λ, Σ | Y, X) d Λ d Σ .$

Сэмплер Гиббса с байесовым увеличением данных

Gibbs sampler with Bayesian data augmentation является Цепью Маркова метод выборки Монте-Карло, который чертит от апостериорного распределения параметров и ненаблюдаемых данных об ответе, учитывая наблюдаемые данные.

Рассмотрите эти наборы индексов:

I = {(i, j) | i = 1, …, m +τ, j = 1, …, m +τ}, вселенная, содержащая все пары индекса (i, j) непредварительных выборочных данных и горизонта прогноза. Y (I) представляет целые непреддемонстрационные данные об ответе включая любых заполнителей (NaN значения) для недостающих наблюдений и ненаблюдаемых значений в горизонте прогноза.
U = {(i, j) ∈ I | Y (i, j) отсутствует или ненаблюдаемый}, набор соответствия пар индекса пропавшим без вести или ненаблюдаемым данным об ответе. Y (U) является набором заполнителей и Y (U^c) набор наблюдаемых данных.

simsmooth симулирует от апостериорного распределения недостающих данных об ответе, коэффициентов и инновационной ковариационной матрицы $π (Y (U), Λ, Σ | Y (U^{c}), X)$ следующим этот сэмплер Гиббса.

Создайте безошибочную наблюдением модель в пространстве состояний путем применения заданного VAR (p) структура к уравнениям состояния. Примените начальные значения параметров Λ⁽⁰⁾ и Σ⁽⁰⁾ (Coeff0 и Sigma0). Получившаяся модель является условным следующим прогнозирующим распределением π (Y (U) | Λ⁽⁰⁾,Σ⁽⁰⁾, Y (U^cX.
Во время итерации j:
1. Симулируйте недостающие данные об ответе Y (U)^(j) от π (Y (U) | Λ^(j-1),Σ^(j-1), Y (U^cX. Выполнять это действие, simsmooth использует более сглаженную симуляцию модели в пространстве состояний (см. simsmooth функция ssm объект модели). simsmooth хранилища Y (U)^(j) в выходе NaNDraws.
2. Составьте увеличенный набор данных Y (I)^(j) = Y (U)^(j) ∪ Y (U^c).
3. Чертите коэффициенты Λ^(j) и инновационная ковариационная матрица Σ^(j) из условной следующей модели Bayesian VAR с увеличенными данными π (Λ,Σ | Y (I)^(j)X. simsmooth хранилища Λ^(j) и Σ^(j) в выходных параметрах CoeffDraws и SigmaDraws, соответственно.
Среднее и стандартное отклонение следующего прогнозирующего распределения π (Y (U) | Λ,Σ, Y (U^c), X), среднее и стандартное отклонение серии ничьих {Y (U)^(j)}. simsmooth хранит статистику в выходных параметрах YMean и YStd.

После удаления электротермотренировки (Burnin) и утончение выборки (Thin), simsmooth хранит остающийся набор ничьих и вычисляет следующую статистику из него.

Советы

Симуляция Монте-Карло подвергается изменению. Если simsmooth симуляция Монте-Карло использования, затем оценивает, и выводы могут варьироваться, когда вы вызываете simsmooth многократно при на вид эквивалентных условиях. Чтобы воспроизвести результаты оценки, установите seed случайных чисел при помощи rng перед вызовом simsmooth.

Алгоритмы

Этот рисунок показывает как simsmooth уменьшает выборку при помощи значений NumDraws, Thin, и BurnIn. Прямоугольники представляют последовательные ничьи от распределения. simsmooth удаляет белые прямоугольники из выборки. Остающийся NumDraws черные прямоугольники составляют выборку.
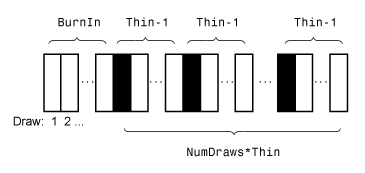
simsmooth не возвращает начальные значения по умолчанию, которые это генерирует.

Ссылки

[1] Литтермен, Роберт Б., "Предсказывающий с Байесовыми Векторными Авторегрессиями: Пять Лет опыта". Журнал Бизнес-и Экономической статистики 4, № 1 (январь 1986): 25–38. https://doi.org/10.2307/1391384.

Смотрите также

Объекты

normalbvarm | conjugatebvarm | semiconjugatebvarm | diffusebvarm | empiricalbvarm

Документация

simsmooth

Синтаксис

Описание

Примеры

Симулируйте параметры от апостериорного распределения при наличии отсутствующих значений

Смотрите увеличенные данные

Настройте опции выборки более сглаженной симуляции

Задайте содействующие начальные значения для более сглаженной симуляции

Предскажите ответы от следующего прогнозирующего распределения

Оцените условные прогнозы

Предскажите модель VARX

Входные параметры

PriorMdl — Предшествующая модель Bayesian VAR conjugatebvarm объект модели | semiconjugatebvarm объект модели | diffusebvarm объект модели | normalbvarm объект модели

Y — Наблюдаемый многомерный ряд ответа числовая матрица

Аргументы name-value

Y0 — Преддемонстрационные данные об ответе числовая матрица

X — Данные о предикторе числовая матрица

NumDraws — Количество случайных ничьих1 (значение по умолчанию) | положительное целое число

BurnIn — Количество ничьих, чтобы удалить с начала выборки0 (значение по умолчанию) | неотрицательный скаляр

Thin — Настроенный множитель объема выборки1 (значение по умолчанию) | положительное целое число

Coeff0 — Начальное значение коэффициентов модели VAR для сэмплера Гиббса числовой вектор-столбец

Sigma0 — Начальное значение инновационной ковариационной матрицы для сэмплера Гиббса положительная определенная числовая матрица

Выходные аргументы

CoeffDraws — Симулированные коэффициенты модели VAR числовая матрица

SigmaDraws — Симулированные инновационные ковариационные матрицы массив положительных определенных числовых матриц

NaNDraws — Обвинения для недостающих данных об ответе числовая матрица

YMean — Увеличенные данные об ответе числовая матрица

YStd — Стандартные отклонения следующего прогнозирующего распределения числовая матрица

Больше о

Байесова векторная авторегрессия (VAR) модель

Следующее прогнозирующее распределение

Сэмплер Гиббса с байесовым увеличением данных

Советы

Алгоритмы

Ссылки

Смотрите также

Объекты

Функции

Документация Econometrics Toolbox

Поддержка

`PriorMdl` — Предшествующая модель Bayesian VAR
`conjugatebvarm` объект модели | `semiconjugatebvarm` объект модели | `diffusebvarm` объект модели | `normalbvarm` объект модели

`Y` — Наблюдаемый многомерный ряд ответа
числовая матрица

`Y0` — Преддемонстрационные данные об ответе
числовая матрица

`X` — Данные о предикторе
числовая матрица

`NumDraws` — Количество случайных ничьих
1 (значение по умолчанию) | положительное целое число

`BurnIn` — Количество ничьих, чтобы удалить с начала выборки
0 (значение по умолчанию) | неотрицательный скаляр

`Thin` — Настроенный множитель объема выборки
1 (значение по умолчанию) | положительное целое число

`Coeff0` — Начальное значение коэффициентов модели VAR для сэмплера Гиббса
числовой вектор-столбец

`Sigma0` — Начальное значение инновационной ковариационной матрицы для сэмплера Гиббса
положительная определенная числовая матрица

`CoeffDraws` — Симулированные коэффициенты модели VAR
числовая матрица

`SigmaDraws` — Симулированные инновационные ковариационные матрицы
массив положительных определенных числовых матриц

`NaNDraws` — Обвинения для недостающих данных об ответе
числовая матрица

`YMean` — Увеличенные данные об ответе
числовая матрица

`YStd` — Стандартные отклонения следующего прогнозирующего распределения
числовая матрица