Создайте нечеткие системы Используя пользовательские функции

Создайте нечеткие системы вывода Используя пользовательские функции в Fuzzy Logic Designer

Когда вы создаете нечеткую систему вывода, как описано в Нечетком Процессе Вывода, можно заменить встроенные функции принадлежности, функции вывода или обоих с пользовательскими функциями. В этом разделе вы изучаете, как создать нечеткую систему вывода с помощью пользовательских функций в приложении Fuzzy Logic Designer.

Создавать нечеткую систему вывода с помощью пользовательских функций в приложении Fuzzy Logic Designer:

Открытый Fuzzy Logic Designer. В MATLAB^® командная строка, введите следующую команду.
```
fuzzyLogicDesigner
```
Задайте количество вводов и выводов нечеткой системы, как описано в Fuzzy Logic Designer.
Создайте пользовательские функции принадлежности и замените встроенные функции принадлежности на них, как описано в Задают Пользовательские Функции принадлежности.
Функции принадлежности задают, как каждая точка во входном пространстве сопоставлена со значением членства между 0 и 1.
Создайте правила с помощью Редактора Правила, как описано в Редакторе Правила.
Правила задают логическое отношение между входными параметрами и выходными параметрами.
Создайте пользовательские функции вывода и замените встроенные функции вывода на них, как описано в Задают Пользовательские Функции Вывода.
Методы вывода включают AND, OR, значение, агрегацию и методы дефаззификации. Это действие генерирует выходные значения для нечеткой системы.
Следующий рисунок показывает пример задачи расчета чаевых, где встроенный Implication, Aggregation и функции Defuzzification заменяются пользовательскими функциями, customimp, customagg, и customdefuzz, соответственно.
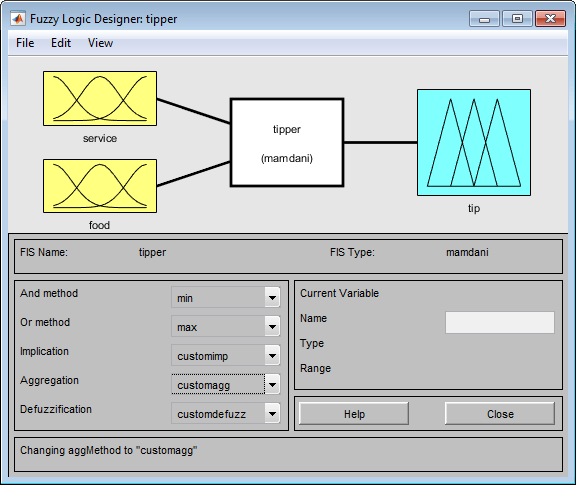
Выберите View> Surface , чтобы просмотреть вывод нечеткой системы вывода в Поверхностном Средстве просмотра, как описано в Поверхностном Средстве просмотра.

Задайте пользовательские функции принадлежности

Можно создать пользовательские функции принадлежности и использовать их в нечетком процессе вывода. Значения этих функций должны находиться между 0 и 1. Для получения дополнительной информации о свойствах функций принадлежности смотрите Функции принадлежности.

Создать пользовательскую функцию принадлежности и заменить встроенную функцию принадлежности:

Создайте функцию MATLAB и сохраните ее в своей текущей рабочей папке.

Чтобы изучить, как создать функции MATLAB, см. Скрипты по сравнению с Функциями.

Следующий код является примером многоступенчатой пользовательской функции принадлежности, custmf1, это зависит от восьми параметров между 0 и 10.

% Function to generate a multi-step custom membership function
% using 8 parameters for the input argument x
function out = custmf1(x,params)

for i = 1:length(x)
    if x(i) < params(1)
        y(i) = params(1);
    elseif x(i) < params(2)
        y(i) = params(2);
    elseif x(i) < params(3)
        y(i) = params(3);
    elseif x(i) < params(4)
        y(i) = params(4);
    elseif x(i) < params(5)
        y(i) = params(5);
    elseif x(i) < params(6)
        y(i) = params(6);
    elseif x(i) < params(7)
        y(i) = params(7);
    elseif x(i) < params(8)
        y(i) = params(8);
    else
        y(i) = 0;
    end
end

out = 0.1*y'; % Scale the output to lie between 0 and 1.

end

Откройте приложение Fuzzy Logic Designer.
```
fuzzyLogicDesigner
```
Fuzzy Logic Designer открывается именем FIS по умолчанию, Untitled, и содержит вход того, input1, и один выход, output1.
В Fuzzy Logic Designer выберите Edit> Membership Functions, чтобы открыть Редактор Функции принадлежности.
Три функции принадлежности треугольной формы для input1 отображены по умолчанию.
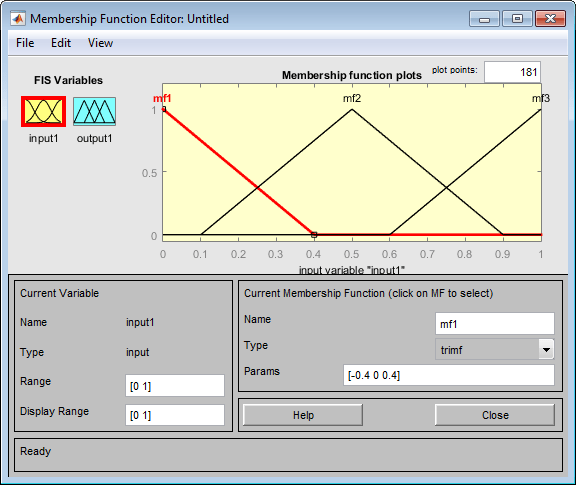
Заменять функцию принадлежности по умолчанию на пользовательскую функцию в Редакторе Функции принадлежности:
1. Выберите Edit> Remove All MFs, чтобы удалить функции принадлежности по умолчанию для input1.
2. Выберите Edit> Add Custom MF, чтобы открыть диалоговое окно Custom Membership Function.
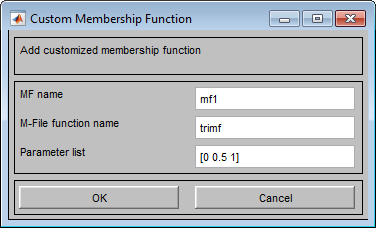
Задавать пользовательскую функцию, в диалоговом окне Custom Membership Function:
1. В поле MF name задайте имя для пользовательской функции принадлежности. В данном примере используйте имя customMF1
  
  Примечание
  При добавлении дополнительных пользовательских функций принадлежности задайте различный MF name для каждой функции.
2. В поле M-file function name задайте имя пользовательского файла функции принадлежности.
3. В Parameter list задайте вектор из параметров. Поскольку этот пример использует векторный [0 1 2 4 6 8 9 10].
  Эти значения определяют форму и положение функции принадлежности, и функция выполнена с помощью этих значений параметров.
  Примечание
  Длина вектора параметра должна быть больше или быть равна количеству параметров в пользовательской функции принадлежности.
  Используя custmf1 пример на шаге 1, диалоговое окно Custom Membership Function выглядит похожим на следующую фигуру.
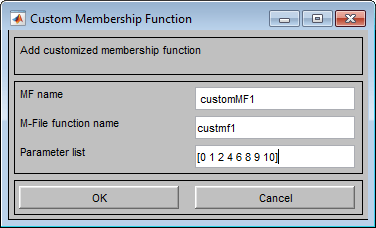
4. Нажмите OK, чтобы добавить пользовательскую функцию принадлежности.
5. Задайте и Range и Display Range, чтобы быть [0 10] совпадать с областью значений пользовательской функции принадлежности.
Редактор Функции принадлежности отображает пользовательский график функции принадлежности.

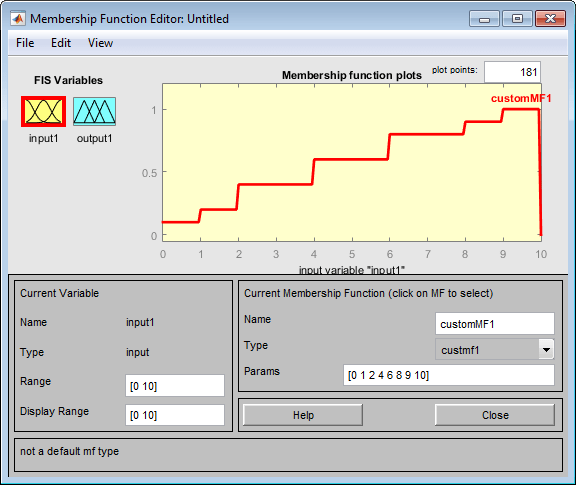
Это действие также добавляет пользовательскую функцию принадлежности в Средство просмотра Правила и делает его доступным для создания правил для нечеткого процесса вывода. Чтобы просмотреть пользовательскую функцию в Средстве просмотра Правила, выберите Edit> Rules или в Fuzzy Logic Designer или в Редакторе Функции принадлежности.
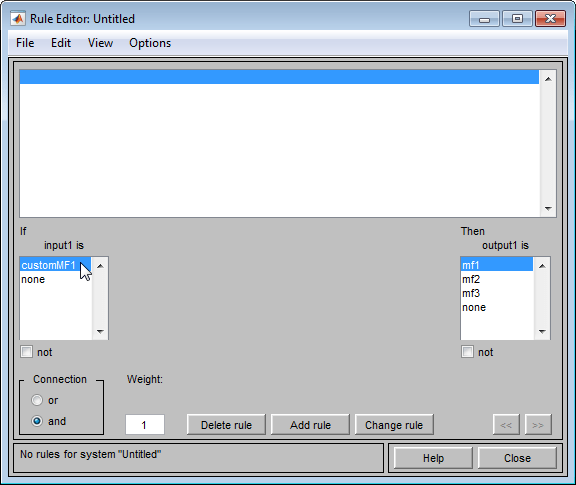
Чтобы добавить пользовательские функции принадлежности для output1, выберите его в Редакторе Функции принадлежности и повторных шагах 4 и 5.

Можно также добавить пользовательскую функцию принадлежности в FIS в командной строке MATLAB. Например, чтобы добавить custmf1 к первой входной переменной, input1 из FIS, myFIS, и назовите его customMF1, введите следующее:

myFIS = addMF(myFIS,"input1","custmf1",[0 1 2 4 6 8 9 10],'Name',"customMF1");

Задайте пользовательские функции вывода

Можно заменить встроенный AND, OR, значение, агрегацию и методы вывода дефаззификации с пользовательскими функциями. После того, как вы создаете пользовательскую функцию вывода, сохраняете ее в вашей текущей рабочей папке. Чтобы изучить, как создать нечеткие системы с помощью пользовательских функций вывода, смотрите раздел Build Fuzzy Inference Systems Using Custom Functions in Fuzzy Logic Designer.

Инструкции для создания и определения функций для создания нечетких систем вывода описаны в следующих разделах.

Создайте пользовательский AND и функции OR
Создайте пользовательские функции значения
Создайте пользовательские функции агрегации
Создайте пользовательские функции дефаззификации
Задайте пользовательские функции вывода в нечеткой системе вывода

Создайте пользовательский AND и функции OR

Пользовательский AND и функции вывода OR должны работать по столбцам с матрицей, таким же образом как функции MATLAB maxmin, или prod.

Для строки или вектор-столбца x, min(x) возвращает минимальный элемент.

x = [1 2 3 4];
min(x)

ans =
     1

Для матричного x, min(x) возвращает вектор-строку, содержащий минимальный элемент из каждого столбца.

x = [1 2 3 4;5 6 7 8;9 10 11 12];
min(x)

ans =
     1     2     3     4

Для массивов N-D, min(x) действует по первому неодноэлементному измерению.

Функциональный min(x,y) возвращает массив, который является тем же размером как x и y с минимальными элементами от x или y. Любой из входных параметров может быть скаляром. Функционирует, такие как max, и prod действуйте подобным образом.

В тулбоксе методы значения AND выполняют поэлементно операцию над матрицей, похожую на функцию MATLAB min(x,y).

a = [1 2; 3 4];
b = [2 2; 2 2];
min(a,b)

ans = 
    1     2
    2     2

Методы значения OR выполняют поэлементно операцию над матрицей, похожую на функцию MATLAB max(x,y).

Создайте пользовательские функции значения

Пользовательские функции значения должны управлять таким же образом как функции MATLAB maxmin, или prod. Вашей пользовательской функцией значения должен быть T - норма нечеткая перекрестная операция. Для получения дополнительной информации смотрите Дополнительные Нечеткие Операторы.

Функция значения должна поддержать или одни или два входных параметров, потому что программное обеспечение вызывает функцию двумя способами:

Вычислить выходные значения нечеткого множества с помощью силы увольнения всех правил и соответствующих выходных функций принадлежности. В этом случае программное обеспечение вызывает функцию значения использование двух входных параметров, похожих на следующий пример:
```
impvals = customimp(w,outputmf)
```
- w — Увольнение силы нескольких правил в виде nr-by-ns матрица. Здесь, nr является количеством правил, и ns является количеством отсчетов выходных функций принадлежности.
  w(:,j) = w(:,1) для всего j. w(i,1) сила увольнения i^th правило.
- outputmf — Выведите значения функции принадлежности в виде nr-by-ns матрица. Здесь, nr является количеством правил, и ns является количеством отсчетов выходных функций принадлежности.
  outputmf(i,:) содержит данные i^th выведите функцию принадлежности.
Вычислить выход нечеткое значение с помощью силы увольнения одного правила и соответствующей выходной функции принадлежности, для данной выборки. В этом случае программное обеспечение вызывает функцию значения использование входа того, похожего на следующий пример:
```
impval = customimp([w outputmf])
```
w и outputmf скалярные значения, представляющие силу увольнения правила и соответствующего выходного значения функции принадлежности, для данной выборки.

Следующее является примером ограниченного произведения пользовательская функция значения с бинарным отображением $T (a, b) = \max {0, a + b - 1}$ . [1]

function y = customimp(x1,x2)

if nargin == 1
    % x1 assumed to be non-empty column vector or matrix.    
    minVal = zeros(1,size(x1,2));
    y = ones(1,size(x1,2));    
 
    for i = 1:size(x1,1)
        y = max(minVal,sum([y;x1(i,:)])-1);
    end
else    
    % x1 and x2 assumed to be non-empty matrices.                  
    minVal = zeros(1,size(x1,2));
    y = zeros(size(x1));
  
    for i = 1:size(x1,1)
        y(i,:) = max(minVal,sum([x1(i,:);x2(i,:)])-1);
    end    
end

end

Примечание

Пользовательские функции значения не поддерживаются для Sugeno-систем-типов.

Создайте пользовательские функции агрегации

Пользовательские функции агрегации должны управлять таким же образом как функции MATLAB maxmin, или prod и должен иметь форму y = customagg(x). Вашей пользовательской функцией значения должен быть T-conorm (S - норма) нечеткая перекрестная операция. Для получения дополнительной информации смотрите Дополнительные Нечеткие Операторы.

x является nv-by-nr матрица, которая является списком усеченных выходных функций, возвращенных методом значения для каждого правила. nv является количеством выходных переменных, и nr является количеством правил. Выход метода агрегации является одним нечетким множеством для каждой выходной переменной.

Следующее является примером ограниченной суммы пользовательская функция агрегации с бинарным отображением $S (a, b) = \min {a + b, 1}$ . [1]

function y = customagg(x)

maxVal = ones(1,size(x,2));
y = zeros(1,size(x,2));

for i = 1:size(x,1)
    y = min(maxVal,sum([y;x(i,:)]));
end

end

Примечание

Пользовательские функции агрегации не поддерживаются для Sugeno-систем-типов.

Создайте пользовательские функции дефаззификации

Пользовательские функции дефаззификации должны иметь форму y = customdefuzz(x,ymf), где x вектор из значений во входном диапазоне функции принадлежности и ymf содержит значения функции принадлежности для каждого x значение.

Следующее является примером пользовательской функции дефаззификации:

function defuzzfun = customdefuzz(x,ymf)

total_area = sum(ymf);
defuzzfun = sum(ymf.*x)/total_area;

end

Примечание

Пользовательские функции дефаззификации не поддерживаются для Sugeno-систем-типов.

Задайте пользовательские функции вывода в нечеткой системе вывода

После того, как вы создадите и сохраните пользовательскую функцию вывода, можно задать функцию в нечеткой системе вывода в командной строке или использовании Fuzzy Logic Designer.

Чтобы задать пользовательские функции вывода в Fuzzy Logic Designer, используйте следующие шаги.

Примечание

Для того, чтобы указать, что пользовательский вывод функционирует в Fuzzy Logic Designer, необходимо сначала добавить по крайней мере одно правило в FIS.

В нижней левой панели Fuzzy Logic Designer выберите Custom в выпадающем меню, соответствующем методу вывода, для которого вы хотите задать пользовательскую функцию.
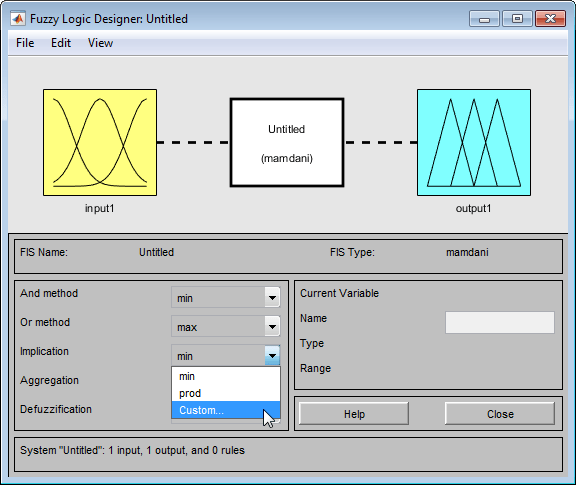
Выполнение так открывает диалоговое окно, где вы задаете имя пользовательской функции вывода.
В поле Method name задайте имя пользовательской функции вывода и нажмите ОК.
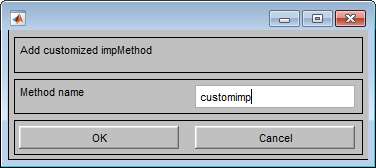
Пользовательская функция заменяет встроенную функцию при создании нечеткой системы вывода.
Чтобы задать пользовательские функции для других методов вывода, повторите шаги 1 и 2.

Задавать пользовательский вывод функционирует для FIS (myFIS) в командной строке MATLAB, набор соответствующее свойство объекта FIS к имени функции вывода. Например, чтобы добавить пользовательское:

Метод дефаззификации, ввести
```
myFIS.DefuzzificationMethod = "customdefuzz";
```
где customdefuzz имя пользовательской функции дефаззификации.
Метод значения, ввести
```
myFIS.ImplicationMethod = "customimp";
```
где customimp имя пользовательской функции значения.
Метод агрегации, ввести
```
myFIS.AggregationMethod = "customagg";
```
где customagg имя пользовательской функции агрегации.

Задайте пользовательские функции сокращения типа

Для типа 2 нечеткие системы вывода можно задать пользовательскую функцию сокращения типа. Эта функция должна иметь форму y = customtr(x,umf,lmf), где x вектор из значений во входном диапазоне функции принадлежности. umf и lmf соответствующие значения верхней и более низкой функции принадлежности для каждого x значение. Выход y двухэлементный вектор-строка из центроидов [_cL, _cR].

Для получения дополнительной информации о сокращении типа смотрите Тип 2 Нечеткие Системы Вывода.

По умолчанию тип 2 системы Sugeno поддерживает только средневзвешенную форму сокращения типа. Следующая пользовательская функция сокращения типа реализует форму взвешенной суммы сокращения типа для системы Sugeno.

function y = customtr(x,umf,ymf)

y = zeros(1,2);

y(1) = sum(x.*umf);
y(2) = sum(x.*lmf);

end

Чтобы задать пользовательское сокращение типа функционируют для FIS (myFIS) в командной строке MATLAB ввести

myFIS.DTypeReductionMethod = "customtr";

где customtr имя пользовательской функции дефаззификации.

Используйте пользовательские функции в генерации кода

Можно использовать пользовательские функции в нечетких системах вывода, для которых вы генерируете код. Для получения дополнительной информации о генерации кода для нечетких систем смотрите, Развертывают Нечеткие Системы Вывода.

Если вы используете недвойной тип данных для своего сгенерированного кода, необходимо распространить тип данных от входных параметров пользовательской функции к выходному аргументу. Например, следующая пользовательская функция агрегации обеспечивает тип данных x в y использование ones и zeros с 'like' аргумент.

function y = customagg(x)

maxVal = ones(1,size(x,2),'like',x);
y = zeros(1,size(x,2),'like',x);

for i = 1:size(x,1)
    y = min(maxVal,sum([y;x(i,:)]));
end

end

Для получения дополнительной информации о записи функций, которые поддерживают генерацию кода C/C++, смотрите, что MATLAB Программирует для Генерации кода (MATLAB Coder).

Ссылки

[1] Mizumoto, Masaharu. ‘Графические Представления Нечетких Соединительных слов, Второй части: Случаи Компенсационных Операторов и Самодвойственные Операторы. Нечеткие множества и Системы 32, № 1 (август 1989): 45–79. https://doi.org/10.1016/0165-0114 (89) 90087-0.

Смотрите также

Fuzzy Logic Designer

Документация