Настройки по умолчанию не могут найти, что глобальный минимум — добавляет границы
GlobalSearch с границами и большим количеством стартовых точек
MultiStart с обычной сеткой и многообещающими стартовыми точками
Нахождение стартовой точки в области притяжения глобального минимума может затруднить, когда область мала или когда вы не уверены в местоположении минимума. Чтобы решить этот тип проблемы, вы можете:
Добавьте разумные границы
Возьмите огромное количество случайных стартовых точек
Сделайте методическую сетку стартовых точек
Для неограниченной проблемы возьмите широко рассеянные случайные стартовые точки
Этот пример показывает эти методы и некоторые варианты.
Функция –sech (x) является почти 0 для всего |x | > 5, и –sech (0) = –1. Примером является двумерная версия функции sech с одним минимумом в [1,1], другой в [1e5,-1e5]:
f (x, y) = –10sech (|x – (1,1) |) – 20sech (.0003 (|x – (1e5, –1e5) |) – 1.
f имеет глобальный минимум –21 в (1e5, –1e5), и локальный минимум –11 в (1,1).
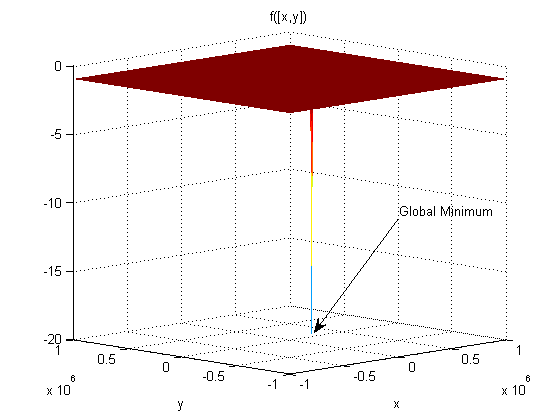
Минимум в (1e5, –1e5) показывает узким скачком. Минимум в (1,1) не показывает, поскольку это является слишком узким.
Следующие разделы показывают различные методы поиска глобального минимума. Некоторые методы не успешны на этой проблеме. Тем не менее, вы можете найти каждый метод полезным для различных проблем.
GlobalSearch и MultiStart не может найти глобальное минимальное значение по умолчанию использования глобальными опциями, поскольку компоненты стартовой точки по умолчанию находятся в области значений (–9999,10001) для GlobalSearch и (–1000,1000) для MultiStart.
С дополнительными границами –1e6 и 1e6 в problem, GlobalSearch обычно не находит глобальный минимум:
x1 = [1;1];x2 = [1e5;-1e5];
f = @(x)-10*sech(norm(x(:)-x1)) -20*sech((norm(x(:)-x2))*3e-4) -1;
opts = optimoptions(@fmincon,'Algorithm','active-set');
problem = createOptimProblem('fmincon','x0',[0,0],'objective',f,...
'lb',[-1e6;-1e6],'ub',[1e6;1e6],'options',opts);
gs = GlobalSearch;
rng(14,'twister') % for reproducibility
[xfinal,fval] = run(gs,problem)
GlobalSearch stopped because it analyzed all the trial points.
All 32 local solver runs converged with a positive
local solver exit flag.
xfinal =
1.0000 1.0000
fval =
-11.0000Чтобы найти глобальный минимум, можно искать больше точек. Этот пример использует 1e5 стартовые точки и MaxTime из 300 с:
gs.NumTrialPoints = 1e5; gs.MaxTime = 300; [xg,fvalg] = run(gs,problem) GlobalSearch stopped because maximum time is exceeded. GlobalSearch called the local solver 2186 times before exceeding the clock time limit (MaxTime = 300 seconds). 1943 local solver runs converged with a positive local solver exit flag. xg = 1.0e+04 * 10.0000 -10.0000 fvalg = -21.0000
В этом случае, GlobalSearch найденный глобальным минимумом.
В качестве альтернативы можно искать использование MultiStart со многими стартовыми точками. Этот пример использует 1e5 стартовые точки и MaxTime из 300 с:
ms = MultiStart(gs);
[xm,fvalm] = run(ms,problem,1e5)
MultiStart stopped because maximum time was exceeded.
MultiStart called the local solver 17266 times before exceeding
the clock time limit (MaxTime = 300 seconds).
17266 local solver runs converged with a positive
local solver exit flag.
xm =
1.0000 1.0000
fvalm =
-11.0000В этом случае, MultiStart не удалось найти глобальный минимум.
Можно также использовать MultiStart искать неограниченную область, чтобы найти глобальный минимум. Снова, вам нужны много стартовых точек, чтобы иметь хороший шанс нахождения глобального минимума.
Первые пять строк кода генерируют 10 000 широко рассеянных случайных стартовых точек с помощью метода, описанного в Широко Рассеянных Точках для Неограниченных Компонентов. newprob структура задачи с помощью fminunc локальный решатель и никакие границы:
rng(0,'twister') % for reproducibility
u = rand(1e4,1);
u = 1./u;
u = exp(u) - exp(1);
s = rand(1e4,1)*2*pi;
stpts = [u.*cos(s),u.*sin(s)];
startpts = CustomStartPointSet(stpts);
opts = optimoptions(@fminunc,'Algorithm','quasi-newton');
newprob = createOptimProblem('fminunc','x0',[0;0],'objective',f,...
'options',opts);
[xcust,fcust] = run(ms,newprob,startpts)
MultiStart completed the runs from all start points.
All 10000 local solver runs converged with a positive
local solver exit flag.
xcust =
1.0e+05 *
1.0000
-1.0000
fcust =
-21.0000В этом случае, MultiStart найденный глобальным минимумом.
Можно также использовать сетку стартовых точек вместо случайных стартовых точек. Чтобы изучить, как создать обычную сетку для большего количества размерностей, или та, которая имеет небольшие возмущения, видит Регулярную координатную сетку или Встревоженную Сетку.
xx = -1e6:1e4:1e6; [xxx,yyy] = meshgrid(xx,xx); z = [xxx(:),yyy(:)]; bigstart = CustomStartPointSet(z); [xgrid,fgrid] = run(ms,newprob,bigstart) MultiStart completed the runs from all start points. All 10000 local solver runs converged with a positive local solver exit flag. xgrid = 1.0e+004 * 10.0000 -10.0000 fgrid = -21.0000
В этом случае, MultiStart найденный глобальным минимумом.
Создание обычной сетки стартовых точек, особенно в высоких размерностях, может использовать беспорядочный объем памяти или время. Можно отфильтровать стартовые точки, чтобы запустить только тех с маленьким значением целевой функции.
Чтобы выполнить эту фильтрацию наиболее эффективно, напишите свою целевую функцию в векторизованном виде. Для получения информации смотрите Запись Векторизованная Функция или Векторизуйте Функции Цели и Ограничения. Следующий указатель на функцию вычисляет вектор из целей на основе входной матрицы, строки которой представляют стартовые точки:
x1 = [1;1];x2 = [1e5;-1e5];
g = @(x) -10*sech(sqrt((x(:,1)-x1(1)).^2 + (x(:,2)-x1(2)).^2)) ...
-20*sech(sqrt((x(:,1)-x2(1)).^2 + (x(:,2)-x2(2)).^2))-1;Предположим, что вы хотите запустить локальный решатель только для точек, где значение меньше –2. Начните с более плотной сетки, чем в MultiStart с Обычной Сеткой Стартовых точек, затем отфильтруйте все точки с высоким значением функции:
xx = -1e6:1e3:1e6;
[xxx,yyy] = meshgrid(xx,xx);
z = [xxx(:),yyy(:)];
idx = g(z) < -2; % index of promising start points
zz = z(idx,:);
smallstartset = CustomStartPointSet(zz);
opts = optimoptions(@fminunc,'Algorithm','quasi-newton','Display','off');
newprobg = createOptimProblem('fminunc','x0',[0,0],...
'objective',g,'options',opts);
% row vector x0 since g expects rows
[xfew,ffew] = run(ms,newprobg,smallstartset)
MultiStart completed the runs from all start points.
All 2 local solver runs converged with a positive
local solver exit flag.
xfew =
100000 -100000
ffew =
-21В этом случае, MultiStart найденный глобальным минимумом. В smallstartset существует только две стартовых точки, один из которых является глобальным минимумом.