Многоугольники представляют географические объекты, которые покрывают область, такую как континенты, острова и озера. Они могут содержать отверстия или несколько областей. Создайте многоугольник путем листинга вершин, которые задают его контуры без пересечения. Порядок вершин определяет, какие части многоугольника заполнены. Перечислите внешние контуры по часовой стрелке и внутренние контуры против часовой стрелки, такой, что внутренняя часть многоугольника всегда справа от контура.
Отобразите простой многоугольник с одной областью и никакими отверстиями. Во-первых, перечислите его вершины в по часовой стрелке порядок. Закройте многоугольник путем повторения первой вершины в конце списка.
x1 = [0 3 4 1 0]; y1 = [0 1 3 2 0];
Отобразите вершины как многоугольник с помощью mapshow функция путем определения 'DisplayType' как 'polygon'.
mapshow(x1,y1,'DisplayType','polygon')

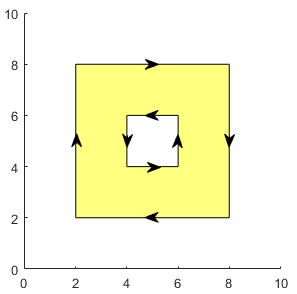
Задайте многоугольники с несколькими областями или отверстиями путем разделения контуров NaN значения. Перечислите вершины внешних контуров в по часовой стрелке порядок и вершины внутренних контуров в против часовой стрелки порядок.
x2 = [0 1 8 6 0 NaN 1 4 2 1 NaN 5 6 7 3 5]; y2 = [0 6 8 2 0 NaN 1 3 5 1 NaN 3 5 7 6 3];
Эти векторы задают многоугольник с одним внешним контуром и двумя внутренними контурами. Контуры разделяются с помощью NaN значения. Проверьте порядок вершины контуров с помощью ispolycw функция. ispolycw функция возвращается 1, когда вершины находятся в по часовой стрелке порядок.
ispolycw(x2,y2)
ans = 1x3 logical array
1 0 0
Отобразите многоугольник. Внутренние контуры создают отверстия в многоугольнике.
figure mapshow(x2,y2,'DisplayType','polygon')

Теперь перечислите вершины для многоугольника с двумя непересекающимися областями. Одна из областей имеет отверстие. Проверьте порядок вершины контуров с помощью ispolycw.
x3 = [0 1 5 6 0 NaN 1 5 4 2 1 NaN 7 6 8 8 7]; y3 = [0 6 7 2 0 NaN 1 3 6 5 1 NaN 4 7 8 7 4]; ispolycw(x3,y3)
ans = 1x3 logical array
1 0 1
Отобразите многоугольник. Внешние контуры создают две непересекающихся области, и внутренний контур создает отверстие.
figure mapshow(x3,y3,'DisplayType','polygon')

В общем случае можно использовать географические координаты, когда вы задаете многоугольники по небольшим областям и вызываете функции, такие как ispolycw. Это верно кроме случаев, где многоугольник переносит полюс или пересекает Антимеридиан.
Например, отобразите Мичиган на карте с помощью многоугольников с географическими координатами. Во-первых, считайте вершины государственных границ.
states = shaperead('usastatehi.shp','UseGeoCoords',true); michigan = states(22); lat = michigan.Lat; lon = michigan.Lon;
Считайте контуры и проверьте их порядок вершины. Использовать ispolycw с географическими координатами перечислите вектор долготы как первый аргумент и вектор широты в качестве второго аргумента. 1 6 выходной массив означает, что существует шесть контуров. Каждый элемент массива равняется 1, что означает, что каждый контур является внешним контуром своей собственной области.
ispolycw(lon,lat)
ans = 1x6 logical array
1 1 1 1 1 1
Отобразите многоугольник на карте с помощью geoshow функция, задавая 'DisplayType' как 'polygon'.
usamap 'Michigan' geoshow(lat,lon,'DisplayType','polygon')

Отсеките многоугольник к пределам широты и долготы Национального парка острова Роял с помощью maptrimp функция. Отобразите отсеченный многоугольник на новой карте.
latlim = [47.8 48.2]; lonlim = [-89.3 -88.4]; [latT,lonT] = maptrimp(lat,lon,latlim,lonlim); figure usamap(latlim,lonlim) geoshow(latT,lonT,'DisplayType','polygon')

Когда вы отображаете многоугольник на Земле, контур делит Землю на две области. Обе из этих областей имеют конечную область, таким образом, любой мог быть внутренней областью многоугольника.

В результате, когда вы проектируете вершины многоугольника на карту с помощью geoshow функция, заполненная область может отличаться, чем вы ожидаете. Изменитесь, какая область заполнена путем инвертирования порядка вершин.
Например, отобразите маленький многоугольник на мировой карте.
lat2 = [0 10 40 30 0]; lon2 = [0 20 30 10 0]; figure worldmap('world') geoshow(lat2,lon2,'DisplayType','polygon')

Внешняя область многоугольника заполнена. Инвертируйте порядок вершин путем применения flip функционируйте к координатным векторам. Затем отобразите многоугольник снова.
lat2f = flip(lat2); lon2f = flip(lon2); figure worldmap('world') geoshow(lat2f,lon2f,'DisplayType','polygon')

Внутренняя область многоугольника заполнена вместо этого.