Интерполяция является методом, чтобы оценить значение функции в местоположении запроса, которое находится в области набора точек выборочных данных. Значение функции вычисляется на основе точек выборочных данных, которые являются самыми близкими к точке запроса. MATLAB® может выполнить два вида интерполяции в зависимости от структуры выборочных данных. Выборочные данные могут сформировать сетку или могут быть рассеяны.
Выборочные данные с координатной сеткой делают интерполяцию более эффективной, потому что организованная структура данных дает возможность для MATLAB находить, что выборочные данные указывают самый близкий к точке запроса. Однако интерполяция данных, имеющий разброс требует Триангуляции Делоне точек данных, и это вводит дополнительный слой расчета. Поэтому, если ваши данные могут быть аппроксимированы как сетка, интерполяция с координатной сеткой обеспечивает существенные сбережения во время вычисления и использование памяти по сравнению с рассеянной интерполяцией.
Два подхода к интерполяции покрыты следующими темами:
Интерполяция Данных С координатной сеткой покрывает 1D интерполяцию и интерполяцию N-D выборочных данных, которые находятся в выровненном осью формате сетки:
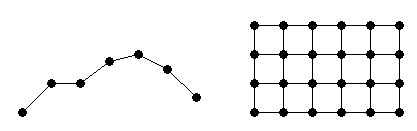
Интерполяция данных, имеющих разброс, касается интерполяции N-D данных, имеющий разброс:

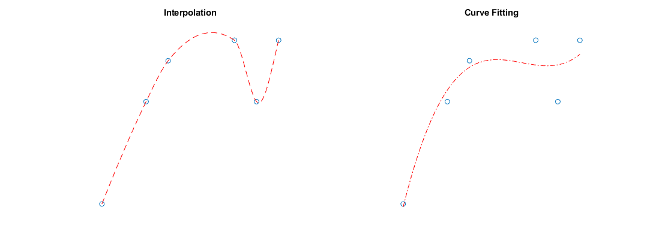
Методы интерполяции, доступные в MATLAB, создают функции интерполяции, которые проходят через точки выборочных данных. Таким образом, если вы запрашиваете функцию интерполяции при демонстрационном местоположении, вы возвращаете точное значение выборочных данных и не приближение. В отличие от этого, изогнитесь и появитесь, алгоритмы подбора не обязательно проходят через точки выборочных данных. Для получения дополнительной информации об аппроксимировании кривыми, смотрите Curve Fitting Toolbox.
В некоторых случаях вы, возможно, должны аппроксимировать сетку для своих данных. Например, сетка может иметь точки, которые простираются вдоль кривых линий. Набор данных как эта сила происходит, если ваши данные являются долготой и базирующейся широтой:
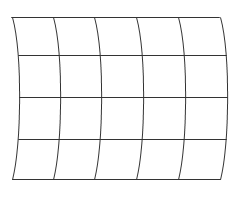
С кривой сеткой вы эффективно имеете дело с набором данных, имеющий разброс и должны использовать более в вычислительном отношении дорогие рассеянные функции интерполяции, чтобы интерполировать значения. Однако несмотря на то, что входные данные не могут быть с координатной сеткой непосредственно, иногда выполнимо аппроксимировать кривую сетку прямыми линиями сетки в соответствующих интервалах:
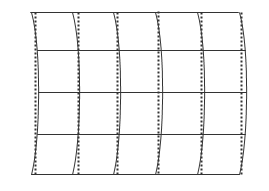
Можно создать аппроксимированную сетку путем создания набора векторов сетки с соответствующим интервалом. Аппроксимация кривой сетки прямыми линиями позволяет вам получать выигрыши в производительности основанной на сетке интерполяции, за счет небольшого искажения данных. Для получения дополнительной информации о создании векторов сетки, смотрите Представления Сетки.
griddedInterpolant | scatteredInterpolant