Данные с координатной сеткой состоят из значений или измерений в расположенных с равными интервалами точках, которые формируют сетку. Данные с координатной сеткой возникают во многих областях, таких как метеорология, рассмотрение и медицинская обработка изображений. В этих областях распространено провести измерения в регулярных пространственных интервалах возможно в зависимости от времени. Эти упорядоченные сетки данных могут расположиться от 1D (для простых временных рядов) к 4-D (для измерения объемов в зависимости от времени) или выше. Некоторые примеры данных с координатной сеткой:
1D: Курсы акций в зависимости от времени
2D: Температура поверхности
3-D: изображение MRI мозга
4-D: Океанские измерения в объеме воды в зависимости от времени
Во всех этих приложениях основанная на сетке интерполяция эффективно расширяет полноценность данных к точкам, где никакие измерения не были проведены. Например, если у вас есть почасовые ценовые данные для запаса, можно использовать интерполяцию, чтобы аппроксимировать цену каждые 15 минут.
MATLAB® обеспечивает несколько инструментов для основанной на сетке интерполяции:
meshgrid и ndgrid функции создают сетки различной размерности. meshgrid может создать 2D или 3-D сетки, в то время как ndgrid может создать сетки с любым количеством размерностей. Эти функции возвращают сетки с помощью различных выходных форматов. Можно преобразовать между этими форматами сетки с помощью pagetranspose (с R2020b) или permute функции, чтобы подкачать первые две размерности сетки.
interp семейство функций включает interp1, interp2, interp3, и interpn. Каждая функция спроектирована, чтобы интерполировать данные с определенным количеством размерностей. interp2 и interp3 используйте сетки в meshgrid формат, в то время как interpn сетки использования в ndgrid формат.
griddedInterpolant объекты поддерживают интерполяцию в любом количестве размерностей для данных в ndgrid формат. Эти объекты также поддерживают многозначную интерполяцию (с R2021a), где каждый узел решетки может иметь несколько значений, сопоставленных с ним.
Существует память и выигрыши в производительности к использованию griddedInterpolant объекты по interp функции. griddedInterpolant предлагает существенные повышения производительности для повторных запросов объекта interpolant, тогда как interp функции выполняют новое вычисление каждый раз, когда они называются. Кроме того, griddedInterpolant хранит точки выборки в эффективном памятью формате (как компактная сетка) и многопоточен, чтобы использовать в своих интересах процессоры многоядерного компьютера.
MATLAB позволяет вам представлять сетку в одном из трех представлений: полная сетка, компактная сетка или сетка по умолчанию. Сетка по умолчанию и компактная сетка используются, в основном, для удобства и повышенной эффективности, соответственно.
full grid - тот, в котором явным образом заданы все точки. Выходные параметры ndgrid и meshgrid задайте полную сетку. Можно создать полные сетки, которые являются uniform, в котором точки в каждой размерности имеют равный интервал или nonuniform, в котором интервал варьируется по одному или нескольким размерностей. Регулярные координатные сетки могут иметь различный интервал в каждой размерности, пока интервал является постоянным в каждой размерности.
| Универсальная форма | Универсальная форма | Неоднородный |
|---|---|---|
|
|
|
Пример универсальной полной сетки:
[X,Y] = meshgrid([1 2 3],[3 6 9 12])
X =
1 2 3
1 2 3
1 2 3
1 2 3
Y =
3 3 3
6 6 6
9 9 9
12 12 12Явным образом определение каждой точки в сетке может использовать большую память, когда вы имеете дело с большими сетками. Представление compact grid является способом обойтись без памяти наверху о полной сетке. Компактное представление сетки хранит только grid vectors (один для каждой размерности) вместо полной сетки. Вместе, векторы сетки неявно задают сетку. На самом деле, входные параметры для meshgrid и ndgrid векторы сетки, и эти функции реплицируют векторы сетки, чтобы сформировать полную сетку. Компактное представление сетки позволяет вам обойти создание сетки и предоставить векторы сетки непосредственно к функции интерполяции.
Например, рассмотрите два вектора, x1 = 1:3 и x2 = 1:5. Можно думать об этих векторах в виде набора координат в x1 направление и набор координат в x2 направление, как так:
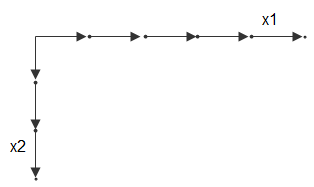
Каждая стрелка показывает на местоположение. Можно использовать эти два вектора, чтобы задать набор узлов решетки, где один набор координат дан x1 и другой набор координат дан x2. Когда векторы сетки реплицированы, они формируют два координатных массива, которые составляют полную сетку:
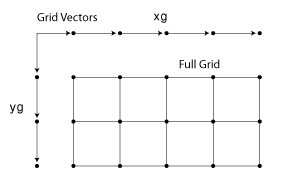
Вашими входными векторами сетки может быть monotonic или nonmonotonic. Монотонные векторы содержат значения, что или увеличьтесь в той размерности или уменьшении в той размерности. С другой стороны немонотонные векторы содержат значения, которые колеблются. Если входной вектор сетки является немонотонным, таким как [2 4 6 3 1], затем [X1,X2] = ndgrid([2 4 6 3 1]) выводит немонотонную сетку. Ваши векторы сетки должны быть монотонными, если вы намереваетесь передать сетку другим функциям MATLAB. sort функция полезна, чтобы гарантировать монотонность.
В некоторых приложениях только значения в узлах решетки важны а не расстояния между узлами решетки. Например, большинство сканов MRI собирает данные, которые расположены равными интервалами во всех направлениях. В случаях как это можно позволить функции интерполяции автоматически генерировать представление default grid, чтобы использовать с данными. Для этого не учтите входные параметры сетки к функции интерполяции. Когда вы не учитываете входные параметры сетки, функция автоматически полагает, что данные находятся на расположенной с интервалами модулем сетке. Функция создает эту расположенную с интервалами модулем сетку, в то время как это выполняется, избавляя вас от необходимости создать сетку самих.
Считайте температурные данные собранными на поверхности в регулярных интервалах на 5 см, расширяя 20 см в каждом направлении. Использование meshgrid создать полную сетку.
[X,Y] = meshgrid(0:5:20)
X =
0 5 10 15 20
0 5 10 15 20
0 5 10 15 20
0 5 10 15 20
0 5 10 15 20
Y =
0 0 0 0 0
5 5 5 5 5
10 10 10 10 10
15 15 15 15 15
20 20 20 20 20(x, y) координаты каждого узла решетки представлены как соответствующие элементы в X и Y матрицы. Первый узел решетки дан [X(1) Y(1)], который является [0 0], следующий узел решетки дан [X(2) Y(2)], который является [0 5], и так далее.
Теперь создайте матрицу, чтобы представлять измерения температуры на сетке и затем отобразить данные на графике как поверхность.
T = [1 1 10 1 1;
1 10 10 10 10;
100 100 1000 100 100;
10 10 10 10 1;
1 1 10 1 1];
surf(X,Y,T)
view(2)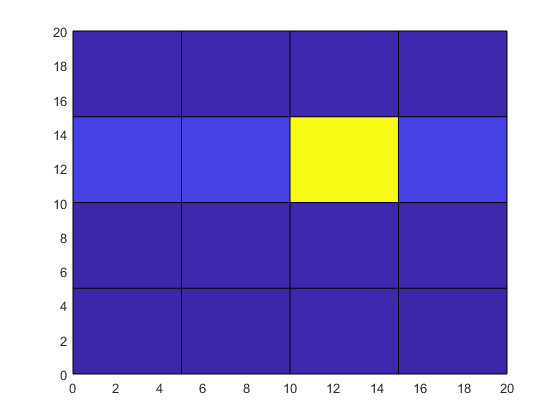
Несмотря на то, что температура в центральном узле решетки является большой, его местоположение и влияние на окружающие узлы решетки не очевидны из необработанных данных.
Чтобы улучшить разрешение данных на коэффициент 10, использовать interp2 интерполировать температурные данные на более прекрасную сетку, которая использует интервалы на 0,5 см. Использование meshgrid снова создать более прекрасную сетку, представленную матрицами Xq и Yq. Затем используйте interp2 с исходной сеткой, температурными данными и новыми узлами решетки, и отображают получившиеся данные на графике. По умолчанию, interp2 линейная интерполяция использования в каждой размерности.
[Xq,Yq] = meshgrid(0:0.5:20); Tq = interp2(X,Y,T,Xq,Yq); surf(Xq,Yq,Tq) view(2)
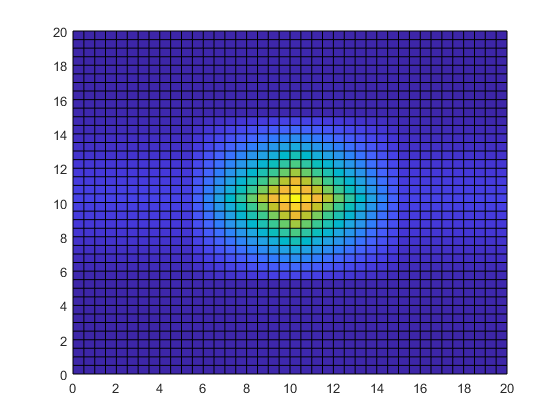
Интерполяция температурных данных добавляет деталь в изображение и значительно улучшает полноценность данных в области измерений.
Основанные на сетке функции интерполяции и объекты в MATLAB предлагают несколько различных методов для интерполяции. При выборе метода интерполяции имейте в виду, что некоторые требуют большей памяти или более длительное время вычисления, чем другие. Вы, возможно, должны обменять эти ресурсы, чтобы достигнуть желаемой гладкости в результате. Следующая таблица дает предварительный просмотр каждого метода интерполяции, применился к тем же 1D данным, и также предоставляет обзор преимуществ, компромиссов и требований для каждого метода.
| Метод | Описание |
|---|---|
|
| Интерполированное значение в точке запроса является значением в самом близком демонстрационном узле решетки.
|
|
| Интерполированное значение в точке запроса является значением в следующем демонстрационном узле решетки.
|
|
| Интерполированное значение в точке запроса является значением в предыдущем демонстрационном узле решетки.
|
|
| Интерполированное значение в точке запроса основано на линейной интерполяции значений в соседних узлах решетки в каждой соответствующей размерности.
|
|
| Интерполированное значение в точке запроса основано на сохраняющей форму кусочной кубичной интерполяции значений в соседних узлах решетки.
|
|
| Интерполированное значение в точке запроса основано на кубичной интерполяции значений в соседних узлах решетки в каждой соответствующей размерности.
|
|
| Интерполированное значение в точке запроса основано на кусочно-линейной функции полиномов со степенью самое большее три оцененных использования значений соседних узлов решетки в каждой соответствующей размерности. Формула Акима изменяется, чтобы избежать перерегулирований.
|
|
| Интерполированное значение в точке запроса основано на кубичной интерполяции значений в соседних узлах решетки в каждой соответствующей размерности.
|
interp1 | interp2 | interp3 | interpn | griddedInterpolant